1. Сов. переходный и непереходный (глагол) смотрите доказывать
1. Докажу, докажешь, совершенный вид (к доказывать). 1. что. Подтвердить какое кто-нибудь положение фактами или доводами. Доказать на деле свою преданность. Доказать правильность своих взглядов цитатами. Доказать теорему. 2. на кого-что. Донести, уличить кого кто-нибудь в чем кто-нибудь ( просторечие ). Он на допросе доказал на своего товарища.
-кажу, -кажешь; причастие страдательное (причастие) прошедшее время доказанный, -зан, -а, -о; совершенный вид
( несовершенный вид доказывать).
1. переходный
Подтвердить истинность, правильность чего -либо фактами, неопровержимыми доводами.
Доказать свою невиновность.
Во всех двадцати главах, которые я до сих пор написал о наших реалистах, я старался доказать, что наше общество не поняло и оклеветало этих людей с чужого голоса. Писарев, Реалисты.
— Докажите же мне это, потому что я не могу и не имею права верить вам на слово. Салтыков-Щедрин, Губернские очерки.
кому.
Какими -либо действиями, поступками и т. падеж дать убедиться кому -либо в чем -либо , заставить поверить.
{Граф:} Что ж, Рыцарь-Несчастие! Хоть раз нам докажи, Что рыцарь, а не трус ты! Блок, Роза и Кре степень
2.
обычно на кого. Про степень Донести на кого -либо
{Колчаковцы} узнали, что Ефрем в той деревне скрывается, доказал кто-то, и начали они по избам подряд шарить. Залыгин, Соленая Падь.
... , пока не . получат такое достаточное условие Pn (x) для (x), что Pn (x)→(x.) и Pn (x) = S(x). Пример : Доказать теорему «Если в четырехугольнике противоположные стороны попарно равны ., то четырехугольник - параллелограмм »; методом ... ... по условию теоремы , а ∟ВОС . = ∟, как вертикальные Далее составляем схему проведенного анализа :. Чтобы доказать -> Надо доказать I ВС || II ∟ВСО =∟, как внутренние накрест лежащие , образованные прямыми ... (Логика)
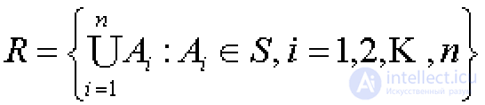... на множествах из Rn называется мерой Лебега на Rn Следующая теорема является аналогом ранее доказанной теоремы о структуре открытых . множеств на числовой прямой Теорема Всякое открытое множество ... ... в Р): m(Е) = m(Р - (Р - Е)) = m(Р) - m(Р. - Е) = m(Р) - μ(G) = m(Р - G). В силу открытости множества G множество F = P - G является. замкнутым Отсюда вытекает утверждение теоремы Задачи Доказать , что система всех конечных подмножеств заданного множества является кольцом . Найти в задаче условие ... (Функциональный анализ)
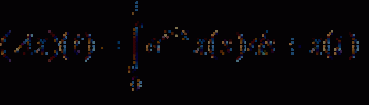... А и В перестановочны Найдите ядра и образы операторов , отображающих ® , заданных формулами . (, ,…) ® (0,, ,…);. (, ,…) ® (, ,…);. (, ,…) ® (, /2 , /3 ,…). Доказать , что оператор , отображающий линейное нормированное пространство Х в фактор-пространство . Х/L (L - линейное пространство , замкнутое по норме ... ... в гильбертовом пространстве Н, то всякий . линейный оператор А может быть задан бесконечной матрицей , где Доказать , что для ограниченности оператора А необходимо и достаточно для. бы некоторого M и любых , выполнялось условие Получить неравенства ... (Функциональный анализ)
... мы не можем воспользоваться теоремой . Хеза для декомпозиции отношения Однако Фейджином Р доказана следующая теорема :. Теорема (Фейджина ) Пусть , , - непересекающиеся множества атрибутов отношения Декомпозиция ... ... отношения на проекции и является декомпозицией без потерь . Докажем что Предположим , что отношение содержит кортежи и. Необходимо доказать , что кортеж также содержится в. По определению проекций , кортеж содержится в , а кортеж содержится ... (Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL)
... людей новых качеств (качеств , которые . у них отсутствовали до вхождения в данную группу )- это:. *А) объективно доказанный факт не осознаваемый субъектом Б) объективно доказанный факт осознаваемый субъектом В) субъективно ... (Социальная психология)
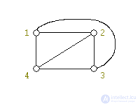... . в Γ1 и Γ2 соответственно , а значит и в Γ3,.причем без пересечения ; следовательно и не были бы конфликтующими . Противоречие Лемма доказана Замечание Из доказанной леммы следует , что, имея сегмент , и еще . сегмент , конфликтующий ... ... нечетный , мы не сможем уложить эти сегменты в. две грани Противоречие Лемма доказана Ну вот , мы наконец-то подошли к тому , чтобы доказать нужную . теорему ... (Алгоритмы и теория алгоритмов)
Комментарии
Оставить комментарий