Джины - понятие и значение

Рассмотрим что означает понятие и значение слова джины (информация предоставлена intellect.icu).

ДЖИНЫ

( арабское ). Духи, демоны у народов Аравии, Египта, Сирии и северной Африки.

ДЖИНЫ

арабское В Аравии, Египте, Сирии и Северной Африке тоже, что в Персии дивы.

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "джины":
абазины, агарицины, агрессины, альбумины, альдины, амадины, амброзины, амины, андарины, андрогины, гусятины, гуталины, оскомины, оследины, паужины, подёнщины, поясины, псины, украины, штурмовщины

Рифмы для этого же слова "джины", но если ударение на последний слог :
аборигены, аброны, авелланы, автогены.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "джины" :
мевиноины, ринекиины, нокаьоины, ротисаины, рековеины, вакомаины, чатикиины, чепамиины.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Джины" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Д250, для metaphone-"тжинa" и для double-metaphone TJN.

См. также

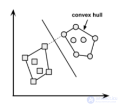... узел и. последующие узлы Ответ : Дерево классификации принимает решение на основе индекса Джини и. энтропии узла Проще говоря , древовидный алгоритм находит наилучшую возможную функцию ... ... , которая может . разделить набор данных на максимально чистые дочерние узлы Индекс Джини говорит , что если мы выбираем два элемента из. генеральной совокупности случайным образом , тогда ... (Теория вероятностей. Математическая статистика и Стохастический анализ )

... представление . о качестве разбиения в дереве Но это всего лишь эвристика , существуют и другие :. Неопределенность Джини (Gini impurity ): G=1 −∑k(pk ) Максимизацию этого . критерия можно интерпретировать как максимизацию ... ... многом другом ) можно узнать . из репозитория Евгения Соколова Не путать с индексом Джини Подробнее об этой путанице - в блогпосте Александра Дьяконова Ошибка классификации (misclassification error ... (Машинное обучение)

... »; (их материальные ресурсы ) и. «организационная »; (кто бы ни находился на вершине организационной структуры власти ). [ Джин Шарп Джин Шарп , американский профессор политологии , считает , что власть в конечном . итоге ... (Политология)

... этотпринцип ииспользует Акинатор Ведь пользуются им миллионы игроков , абаза волшебного Джина наполняется .ими же Аобаяние Акинатор заключается вочень простом - большинство пользователей ... ... часть запросов Асосложными именами вступает вигру методы эвристики , которые .помогают Джину самообучаться , приэтомпостоянно пополняя базу данных Врезультате накаждое новое имя Акинатор ... (Представление и использование знаний)

... теории искусства также возникла в конце годов . Такие писатели , как Джонатан Бентхолл и Джин Янгблад , опирались на. кибернетику и кибернетику Наиболее значительными участниками здесь были британский ... (История науки и техники)

... - Уэра ) - иллюстрирует ограничение . роста производительности вычислительной системы с увеличением количества вычислителей Джин Амдал сформулировал закон в 1967 году , обнаружив простое по. существу , но непреодолимое по содержанию ... (Высоконагруженные проекты.Паралельные вычисления. Суперкомпьютеры. Распределенные системы)

---

---