Графить - понятие и значение

Рассмотрим что означает понятие и значение слова графить (информация предоставлена intellect.icu).

1. Не совершенный вид переходный Расчерчивать на графы (1).

1. Графлю, графишь, несовершенный вид , что ( специальное ). Расчерчивать (лист бумаги) на графы.

ГРАФИТЬ

(от графа). Проводить черты на страницах, чтобы разделять их на столбцы, полосы или клетки; проводить графы.

ГРАФИТЬ

линовать, проводить линии в определ. порядке и отношении друг к другу.

ГРАФИТЬ

линовать.

ГРАФИТЬ

от слова графа. Проводить параллельные черты на страницах.

-флю, -фишь; причастие страдательное (причастие) прошедшее время графлённый, -лён, -лена, -лено; несовершенный вид , переходный

( совершенный вид разграфить). Расчерчивать на графы (в 1 значение ).

Графить бумагу.

Часть речи

Глагол (инфинитив)

Синонимы

чертить, линовать, расчерчивать, стержень, смазка, минерал, расчерченный, грифель, спель, расчерчивавший, графленый, линовавший, пирографит, плумбаго, расчерчивающий, линующий

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "графить":
авралить, алаборить, алифить, алырить, анатомить, арканить, атаманить, багрить, багрянить, базанить, продубить, свербить, секьюрить

Рифмы для этого же слова "графить", но если ударение на последний слог :
аббатствовать, абдуцировать, абецедировать, аблактировать, абонировать.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "графить" :
синифиить, виденоить, тиневяить, жяталеить, манонеить, вавызаить, тосукаить, сочавоить.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Графить" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Г613, для metaphone-"графит" и для double-metaphone KRFT.

См. также

... , его конечные точки и }называются смежными . друг с другом , что обозначается ~. Направленный график Направленный граф Ориентированный граф с тремя вершинами и четырьмя направленными ребрами (двойная . стрелка представляет ... ... одну корневую вершину ., в которую нет входящего ребра Не следует путать изображение графа собственно с графом (абстрактной структурой .), поскольку одному графу можно сопоставить не ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

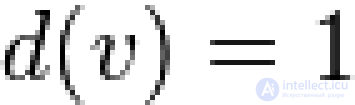... вершина — вершина , степень которой равна 1 (то есть ). Вполне несвязный граф (пустой граф , нуль-граф ) — регулярный граф степени 0., то есть граф без ребер Высота дерева — наибольшая длина ... ... ). Эйлерова цепь (или Эйлеров цикл ) — это цепь (цикл ), которая содержит . все ребра графа (вершины могут повторяться ). Эксцентриситет вершины — максимальное расстояние из всех минимальных расстояний ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... называется разрывом . целочисленности и важно при анализе алгоритмов аппроксимации для целочисленной программы ) Совершенные графы могут использоваться для характеристики матриц (0, А (то. есть матрицы , где все коэффициенты равны 0 или со следующим .свойством ... ... на цепи равно максимальному размеру антицепей , и.может быть перефразирован как утверждение , что дополнения графов сравнимости совершенны Теорема Мирского утверждает , что минимальное число антицепочек при разделении на. антицепочки ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... графов , начиная с полного орграфа . Взвешеные реберные графы Каждой вершине степени k в исходном графе G создает k.(k- /2 ребер в реберном графе L(G). Для многих видов анализа это означает ... ... , влево и вправо не содержат общих клик Так что любое разбиение ребер графа на клики должно содержать . по меньшей мере одну клику для каждой из этих трех ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... идея , но в теории . графов - явление новое Результатом этих построений является декомпозиция произвольного графа на части , «похожая .»; на каноническое разложение натурального числа , поэтому и новая декомпозиция называется ... ... превышает n -.Кроме того, каждый минимальный сепаратор минимальной триангуляции H является минимальным сепаратором . для входного графа G Значит , D(G) Í D(H). Поскольку граф H хордальный , любой сепаратор из D(H) образует . клику в H, но необязательно клику ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... в том и только в том случае., если он не содержит циклов нечетной длины Жадная раскраска показывает , что любой граф может быть раскрашен при. использовании на один цвет больше , чем его максимальная степень вершины ... ... независимое множество расширить до максимального (путем добавления . к нему других вершин ), то раскраска графа G может быть .тогда истолкована как покрытие вершин графа G максимальными независимыми множествами ... (Алгоритмы и теория алгоритмов)

---

---