Алгебраически - понятие и значение

Рассмотрим что означает понятие и значение слова алгебраически (информация предоставлена intellect.icu).

1. Нареч. Алгебраическим способом.

Часть речи

Наречие

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "алгебраически":
авантюристически, автобиографически, автоматически, авторитаристски, авторски, агрономически, агротехнически, адски, академически, акробатически, баски, выпуски, ледоспуски, мракобески, наброски, натаски, обвески, поиски, ряски, хакаски

Рифмы для этого же слова "алгебраически", но если ударение на последний слог :
августинки, автогонки.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "алгебраически" :
накирыски, ноыякески, рякепаски, вйдаьиски, бяраьяски, кабямоски, бокиваски, келамаски.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Алгебраически" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-А421, для metaphone-"алгибраичиски" и для double-metaphone primary : ALJP secondary: ALKP.

См. также

... Алгебраическое уравнение (полиномиальное уравнение , многочленное уравнение ) - уравнение вида где - многочлен от переменных , которые ... ... неизвестными Коэффициенты многочлена обычно берутся из некоторого поля , и тогда уравнение . называется алгебраическим уравнением над полем Степенью алгебраического уравнения называют степень многочлена . Например , уравнение ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)

... xn - a = - Двучленное алгебраическое уравнение степени Решения определяются формулами : где k = 0, 1 ,. , и = 1 ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)

... Алгебраическое уравнение вида : называется возвратным , если его коэффициенты , стоящие на. симметричных относительно середины позициях ... ... середины позициях , равны , то есть если , при k =.0, 1 , …, n Иногда такие уравнения называют симметричными или симметрическими + + +. + + + = - Возвратное (алгебраическое ) уравнение ( ≠ Замена y = x + 1 /x приводит уравнение к. степени ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)

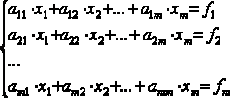... Крамера Метод обратной матрицы . Метод Гаусса Итерационные методы решения линейных алгебраических систем :. Метод простой итерации или метод Якоби . Метод Гаусса - Зейделя Метод ... ... В дальнейшем будем предполагать наличие единственного решения Все методы решения линейных алгебраических задач можно разбить на два . класса : прямые (точные ) и итерационные (приближенные ). Прямые ... (Численные методы)

... + + + bx + a = - Возвратное (алгебраическое ) уравнение Для решения этого уравнения необходимо сделать замену : y = x + 1 ./x, в результате ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)

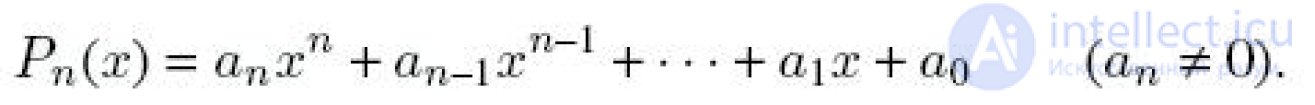... это уравнение так же должно иметь корень η = α. - iβ, причем кратности обоих корней одинаковы Алгебраическое уравнение степени n с целыми коэффициентами ak не может . иметь других рациональных ... ... дроби p/q, причем .p - делитель , и q - делитель an Если an = 1 , тогда все рациональные корни алгебраического уравнения - целые . делители свободного и могут быть легко найдены Любое уравнение ... (СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА)

---

---