Лекция
Привет, Вы узнаете о том , что такое второе начало термодинамики, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое второе начало термодинамики, кпд тепловых машин, цикл карно, двигатель внутреннего сгорания, двс, тепловой двигатель , настоятельно рекомендую прочитать все из категории Молекулярная физика и термодинамика.
В этой главе мы продолжим изучение термодинамических свойств систем. Основная наша цель сейчас - понять, каким образом тепло может быть преобразовано в работу механизмов. Как мы видели, тепловая энергия — это в конечном итоге энергия хаотического движения молекул. Полезная же работа, извлекаемая из различных устройств, имеет упорядоченный характер. Тепловые машины вращают генераторы на электростанциях, приводят в движение транспортные средства. Каким же образом происходят превращения одного вида энергии в другие? Интуитивно ясно, что различные виды энергии чем-то разнятся, даром что все они подчиняются закону сохранения энергии или первому началу термодинамики. В самом деле, очень легко превратить механическую работу в тепло: достаточно потереть друг о друга два деревянных бруска, и они нагреются (говорят, таким образом удается даже зажечь огонь). Упорядоченное периодическое движение брусков превращается при этом в хаотическое движение составляющих их молекул. Но сможете ли вы заставить нагретые бруски истратить часть своей тепловой энергии на возбуждение упорядоченного периодического движения? Словом, в этой главе мы займемся вопросом, с какой эффективностью порядок может быть организован из хаоса.
Среди всех возможных термодинамических процессов, изображаемых на диаграммах состояний, особое место занимают процессы, соответствующие замкнутым кривым (рис. 5.1). В этих процессах физическая система проходит через ряд состояний и возвращается в исходное. Этим и обусловлена важность замкнутых процессов (циклов).
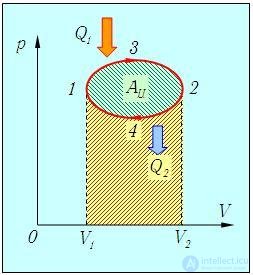
Рис. 5.1. Пример условного замкнутого цикла (направление процесса показано стрелками). Площадь под верхней кривой равна работе, совершаемой системой, а площадь под нижней кривой — работе внешних сил над системой (показана коричневой штриховкой). Разность площадей (показана зеленой штриховкой) равна полной работе, совершенной системой за цикл
Рассмотрим подробнее процесс на рис. 5.1. При расширении газа по «пути» 1-3-2 от минимального (V1) до максимального (V2) объема система совершает положительную работу А132, численно равную площади под верхней кривой. При возвращении системы в исходное состояние по другому пути 2-4-1 paбота А241 совершается над системой. Работа системы отрицательна и по абсолютной величине равна площади под нижней кривой. Алгебраическая сумма этих работ
есть полная работа, совершенная системой за цикл. Ее численная величина равна разности упомянутых площадей, то есть площади, заключенной между верхней и нижней кривыми. Иными словами, полная работа за цикл равна площади, ограниченной данным циклом на диаграмме (р, V), если процесс совершается по часовой стрелке; в противном случае полная работа отрицательна, но ее модуль также равен этой площади.
В ходе осуществления цикла система взаимодействовала с внешней средой, получала и отдавала теплоту. Если обозначить через Q1 количество теплоты, полученное системой, то коэффициент полезного действия (КПД) 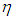 естественно определить как отношение
естественно определить как отношение
|
|
|
(5.1) |
где АЦ — работа за цикл.
КПД часто выражают также в процентах, для чего величину 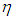 надо умножить на 100 %. Если обозначить через Q2 > 0 количество теплоты, возвращенное системой во внешнюю среду, то разность Q1 – Q2 равна совершенной работе АЦ. Это следует из первого начала термодинамики и из того факта, что при возвращении системы в исходное состояние ее внутренняя энергия также принимает исходное значение, то есть
надо умножить на 100 %. Если обозначить через Q2 > 0 количество теплоты, возвращенное системой во внешнюю среду, то разность Q1 – Q2 равна совершенной работе АЦ. Это следует из первого начала термодинамики и из того факта, что при возвращении системы в исходное состояние ее внутренняя энергия также принимает исходное значение, то есть
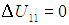
Тогда КПД тепловой машины записывается в виде
|
|
|
(5.2) |
Отсюда видно, что КПД тепловой машины не может быть больше единицы. Это утверждение можно сформулировать как невозможность вечного двигателя первого рода:
|
Невозможно соорудить периодически действующую тепловую машину, которая совершала бы полезную работу в количестве, превышающем получаемую извне энергию. |
Существование такого двигателя противоречило бы закону сохранения энергии. Поскольку ни количество теплоты, ни совершенная системой работа не являются функциями состояния, КПД зависит от данного конкретного цикла, по которому работает тепловая машина.
До сих пор мы рассматривали процесс, соответствующий работе именно тепловой машины. Если повернуть процесс вспять (пустить его против часовой стрелки на рис. 5.1), то мы получим модель холодильной установки. Все стрелки на этом рисунке меняют направления на обратные, система получает от холодильника количество теплоты Q2, и за счет работы внешней силы (электромотора) передает нагревателю большее количество теплоты Q1. Закон сохранения энергии (первое начало термодинамики) требует выполнения равенства
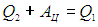
Эффективность холодильной установки можно определить аналогично КПД тепловой машины. Надо только учесть, что полезным теперь является количество отнимаемого тепла Q2, для чего мы совершаем работу АЦ. Поэтому в литературе часто определяют холодильный коэффициент 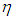 ’ как отношение отнимаемой теплоты к совершаемой при этом работе:
’ как отношение отнимаемой теплоты к совершаемой при этом работе:
|
|
|
(5.3) |
Заметим, что холодильный коэффициент может быть больше единицы. Если мы хотим пользоваться привычным коэффициентом полезного действия, то для холодильной установки естественно определить его как отношение отнятого тепла к переданному во внешнюю среду:
|
|
|
(5.4) |
Такое определение соответствует традиционным взглядам на КПД установок. Действительно, в холодильнике со 100 %-й эффективностью (если бы он был возможен) все количество отнятой теплоты передавалось бы без совершения работы во внешнюю среду. Тогда мы имели бы Q2 = Q1 и 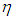 хол = 1. Наоборот, когда мы совершаем какую-то работу, но не отнимаем никакой теплоты, то Q2 = 0 и
хол = 1. Наоборот, когда мы совершаем какую-то работу, но не отнимаем никакой теплоты, то Q2 = 0 и 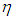 хол = 0.
хол = 0.
Для работы любой тепловой машины по замкнутому циклу необходима внешняя среда, которую условно можно представить себе как два тела — нагреватель, находящийся при температуре Тmах, и холодильник, находящийся при температуре Tmin (Tmin < Тmах). Предполагается, что при контакте с нашей системой температуры нагревателя и холодильника не меняются. При контакте с нагревателем система получает тепло, при контакте с холодильником - отдает его.
В термодинамике существует теорема Карно (рис. 5.2):

Рис. 5.2. Леонар Сади Карно (французский физик и военный инженер)
|
При заданных температурах нагревателя и холодильника максимально возможный КПД тепловой машины не зависит от природы рабочего тела машины и определяется формулой
|
Реализация максимально возможного КПД достигается в так называемом цикле Карно, когда идеальный газ проходит замкнутый цикл, составленный из двух адиабат и двух изотерм (рис. 5.3).
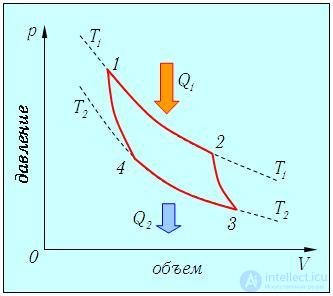
Рис. 5.3. Цикл Карно (обходится по часовой стрелке) — комбинация двух изотерм 1-2, 3-4 и двух адиабат 2-3 и 4-1; теплообмен со средой осуществляется на изотермических участках цикла: на участке 1-2 газ получает теплоту Q1, а на участке 3-4 отдает теплоту Q2
Убедимся, что показанный замкнутый процесс действительно имеет КПД, соответствующий формуле (5.5). Температура системы равна T1 в точках 1, 2 и T2 в точках 3, 4. Значения остальных термодинамических параметров (р, V) будут иметь в качестве индекса номер соответствующей точки на диаграмме. Нам надо вычислить количества полученной Q1, и отданной Q2 теплоты, найти совершенную газом работу АЦ = Q1 – Q2 и определить КПД цикла. Сразу заметим, что на участках 2-3 и 4-1 система не обменивается теплом с внешней средой. Следовательно, теплоту Q1 газ получает на участке 1-2, а теплоту Q2 отдает на участке 3-4. Рассмотрим подробнее различные участки цикла.
См. анимацию «Цикл Карно»
Изотерма 1-2. На этом участке газ находится в контакте с нагревателем и происходит изотермическое расширение от объема V1 до объема V2. Температура Т1 не меняется, следовательно, не изменяется внутренняя энергия, а вся полученная теплота расходуется на совершение газом работы:
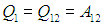
Величину работы газа при изотермическом процессе мы уже вычисляли ранее, так что с учетом формулы (2.13)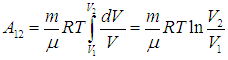 находим
находим
|
|
|
(5.6) |
Адиабата 2-3. Здесь система отсоединяется от нагревателя и не обменивается теплом с внешней средой: Q23 = 0. Газ продолжает расширяться, но уже адиабатно. Работа совершается за счет внутренней энергии газа, и его температура падает до значения Т2. На этом участке цикла нам нужна информация, доставляемая уравнением адиабаты:
|
|
|
(5.7) |
Изотерма 3-4. Система подключается к холодильнику, и газ начинает сжиматься. Внутренняя энергия остается неизменной, над газом совершается работа (А34 < 0), а выделяющееся
тепло
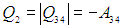
передается холодильнику. Имеем аналогично (5.6)
|
|
|
(5.8) |
Адиабата 4-1. Система отключена от внешней среды и продолжает сжиматься изотермически, что приводит к повышению ее температуры до Т1. В конечном итоге система возвращается в первоначальное состояние. Поскольку точки 4 и 1 лежат на адиабате, получаем связь объемов и температур, аналогичную (5.7):
|
|
|
(5.9) |
Из уравнений (5.7) и (5.9) находим отношения объемов
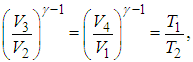
откуда следует, что
|
|
|
(5.10) |
Поэтому отдаваемую холодильнику теплоту Q2 (см. уравнение (5.8)) можно записать как
|
|
|
(5.11) |
Используя выражение (5.6) для теплоты, полученной системой, находим совершенную в ходе цикла работу
|
|
|
(5.12) |
Из проведенного анализа следует также, что максимальная температура в цикле равна Тmах = Т1, а минимальная — Тmin = Т2. Если разделить (5.12) на (5.6), то немедленно получим выражение (5.5) для КПД цикла Карно, из которого выпадают все параметры, кроме температур холодильника и нагревателя.
Пример 1. Котел тепловой станции работает при температуре около t1 = 550 °С. Отработанное тепло отводится к реке при температуре около t2 = 20 °С. Найдем максимально возможный КПД этой станции (рис. 5.4).
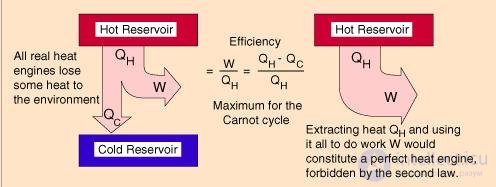
Рис. 5.4. Схема работы тепловой машины Карно
Поскольку в формуле для КПД цикла Карно используются абсолютные температуры, надо перейти от шкалы Цельсия к шкале Кельвина: Т1 = 550 + 273 = 823 К, Т2 = 20 + 273 = 293 К. Теперь находим КПД тепловой станции:
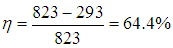
Конечно, реальный КПД станции заметно ниже.
Если цикл Карно осуществить в обратном направлении, то есть против часовой стрелки на рис. 5.2, то для определения эффективности холодильной установки надо использовать формулы (5.3), (5.4) и выражения (5.6), (5.11). Получаем тогда
|
|
|
(5.13) |
Печально, но чем ниже температура внешней среды Т1, тем меньше мы нуждаемся в холодильнике, и тем эффективнее он работает.
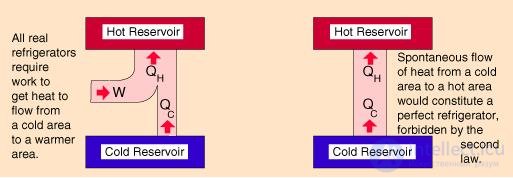
Рис. 5.5. Схема работы холодильной установки
Приведем численный пример. Если кондиционер поддерживает в комнате температуру t2 = 20 °С, а температура наружного воздуха равна t1 = 30 °С, то для холодильного коэффициента имеем
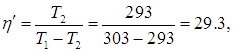
а для КПД холодильника
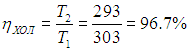
Конечно, на самом деле температура тепловыделяющего элемента больше наружной температуры на 20–30 градусов, так что разность температур может достигать 30–40 градусов, что приводит к значениям
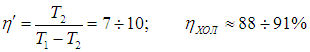
Напомним, что речь идет об идеальных установках, работающих по циклу Карно. Реальный типичный кондиционер потребляет мощность 750 Вт, перекачивая за час около 5 МДж тепловой энергии. Это значит, что за секунду кондиционер совершает работу А = 750 Дж и отнимает у воздуха в комнате теплоту
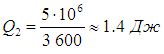
Отсюда находим
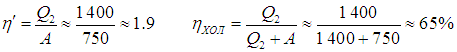
Мы видим, что реальный кондиционер гораздо менее эффективен, нежели идеальный холодильник Карно.
Пример 2. Пусть в домашнем холодильнике поддерживается температура t2 = –3 °С (Т2 = 270 К), а температура в кухне равна t1 = 27 °С (T1 = 300 К). Пусть далее мотор холодильника потребляет мощность N = 200 Вт. Предполагая, что холодильник работает по циклу Карно и что тепловыделяющий элемент имеет температуру окружающего воздуха, определим мощность потока тепловой энергии, перекачиваемой из камеры холодильника в кухню.
За время t мотор совершит работу
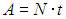
КПД холодильника равен
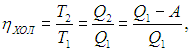
откуда находим количество теплоты, поступающее в кухню в единицу времени:
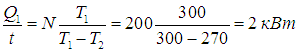
Обратите внимание, что холодильник работает как весьма эффективный обогреватель помещения. Надо только оплачивать потребляемую мотором мощность 200 Вт, а в кухню поступит в 10 раз большая энергия, 90 % которой перекачивается из камеры холодильника (90 % — КПД холодильника в этом примере). Любопытно, что если бы вместо холодильника был включен обогреватель той же мощности, то он нагревал бы помещение в 10 раз слабее.
Наши численные оценки можно рассматривать как пример теплового загрязнения окружающей среды, свойственного технической цивилизации.
Конечно, сравнение лишь двух циклов с циклом Карно не может служить доказательством максимальной (по КПД) эффективности последнего. Но даже если мы переберем все мыслимые циклы, то все равно искомого доказательства не получим. Ведь в цикле Карно в качестве рабочего тела используется идеальный газ. Быть может, если заставить работать какое-либо другое вещество, мы сумеем превзойти КПД цикла Карно? Вообразим, что такая тепловая машина X принципиально возможна, и посмотрим, к каким последствиям это приведет. Используя эту гипотетическую тепловую машину с КПД  х, соорудим новую установку: соединим машину X с холодильной установкой Карно и подсоединим их к одному и тому же нагревателю (находящемуся при температуре Т1) и холодильнику (находящемуся при температуре Т2). Схема установки изображена на рис. 5.6.
х, соорудим новую установку: соединим машину X с холодильной установкой Карно и подсоединим их к одному и тому же нагревателю (находящемуся при температуре Т1) и холодильнику (находящемуся при температуре Т2). Схема установки изображена на рис. 5.6.
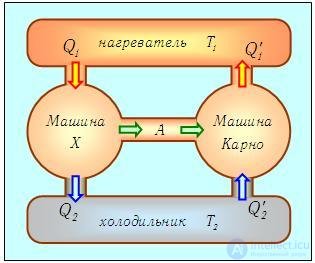
Рис. 5.6. Гипотетическая тепловая машина, позволяющая обосновать невозможность вечного двигателя второго рода
Как будет работать наш агрегат? Машина X забирает теплоту Q1 от нагревателя, часть ее превращает в полезную работу
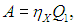
а остаток
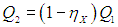
передает холодильнику. Вся полезная работа А (предполагается, что исключены потери энергии) используется для приведения в действие холодильной установки Карно, КПД которой равен
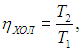
а холодильный коэффициент
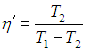
(см. Об этом говорит сайт https://intellect.icu . выражения (5.13)). Это значит, что установка Карно забирает из холодильника теплоту
|
|
|
(5.14) |
и передает нагревателю теплоту
|
|
|
(5.15) |
где, напомним, 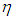 С — КПД тепловой машины Карно.
С — КПД тепловой машины Карно.
В результате действия агрегата из двух машин получился следующий итог. Никакой работы не произведено, так как вся работа от действия тепловой машины X потрачена на приведение в действие холодильной установки Карно. От холодильника отнято количество теплоты
|
|
|
(5.16) |
Точно такое же количество теплоты передано нагревателю: как следует из (5.15),
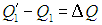
Так что с законом сохранения энергии у нас все в порядке, но если 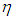 Х >
Х > 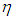 С, то
С, то

Это значит, что наш агрегат без всякой работы внешних сил передал какое-то количество теплоты от холодильника к нагревателю. Казалось бы, что беспокоиться не о чем, раз закон сохранения энергии не нарушен. Но никто в природе не наблюдал таких процессов передачи тепла от холодных тел к горячим, при которых в окружающей среде не происходило каких-либо изменений. В конечном итоге на основе опытных фактов было сформулировано второе начало термодинамики:
|
Невозможны термодинамические процессы, единственным результатом которых был бы переход тепла от тела менее нагретого к телу более нагретому. |
Не следует думать, что второе начало термодинамики запрещает передачу тепла от холодного тела к горячему. Отнюдь нет, в холодильной установке так и происходит. Но ключевое слово в формулировке второго начала — это слово единственный. Передача тепла от холодного тела к нагретому — не единственный результат действия холодильной установки, она связана с внешним источником, за счет работы которого и функционирует.
Многочисленные опыты и наблюдения привели ко второму началу термодинамики и пониманию, что оно является фундаментальным законом природы. Коль скоро это так, то из второго начала следует вывод: КПД любой гипотетической тепловой машины X не превосходит КПД машины Карно, работающей в том же интервале температур:
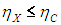
Последнее означает, что минимальная температура рабочего тела машины Х не меньше температуры холодильника машины Карно и максимальная температура рабочего тела машины Х не больше температуры нагревателя машины Карно. Если эти неравенства не выполнены, то соотношение между КПД двух машин может быть любым. Данное обстоятельство явно учтено в комбинированной машине, изображенной на рис. 5.3: у машины Х и машины Карно общие нагреватель и холодильник.
У второго начала термодинамики есть и другая формулировка:
|
Невозможно осуществление периодического процесса, единственным результатом которого было бы получение работы за счет тепла, взятого из одного источника. |
Иными словами, нельзя построить установку, где все тепло Q1, полученное от нагревателя, преобразовывалось бы в полезную работу Ац = Q1. Тогда КПД такой установки (ее называют вечным двигателем второго рода) равнялся бы единице и превысил бы КПД цикла Карно. Таким образом, второе начало термодинамики запрещает существование вечного двигателя второго рода: какое-то количество полученного тепла обязательно должно быть передано другим телам (холодильнику). Изобретателям остается только пожалеть об этом. Как было бы здорово, если бы можно было использовать огромную тепловую энергию, накопленную, скажем, в Мировом океане! Увы, мы вынуждены сжигать топливо, что приводит и к расходованию природных ресурсов, и к выбросу углекислого газа и прочих продуктов сгорания, и к тепловому загрязнению окружающей среды вследствие принципиальной необходимости отводить часть теплоты в атмосферу или водоемы, играющие роль холодильника.
Вопрос о КПД тепловых машин тесно связан с проблемой обратимости термодинамических процессов.
|
Обратимый процесс — это термодинамический процесс, который может быть проведен в обратном направлении через ту же последовательность равновесных состояний, что и в прямом направлении; при этом в окружающей среде не произойдет никаких изменений. |
Обратимость процессов в термодинамике сродни отсутствию трения в механике. Так же как в механике наилучшим механизмом является механизм без трения, так и здесь наилучшей тепловой машиной является обратимая машина. Чтобы показать это, снова обратимся к нашему агрегату на рис. 5.3. Мы не предполагали, что машина X обратима, но получили, что ее КПД не может превышать КПД тепловой машины Карно, работающей в паре с ней в обратном направлении:
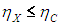
Пусть теперь машина X будет обратимой. Запустим наш агрегат в обратном направлении: машина Карно производит полезную работу, и она используется для запуска машины X как холодильной установки. Но тогда с помощью таких же аргументов мы получим противоположное неравенство
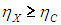
Из двух противоположных неравенств следует единственный вывод: КПД обеих машин равны:
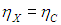
Таким образом, все обратимые тепловые машины имеют одинаковый КПД, совпадающий с КПД машины Карно. Необратимые же машины имеют меньший КПД.
Какие машины в принципе могут быть обратимыми? Мы видели, что тепло может течь только от нагретых тел к холодным. Это и создает необратимость и неравновесность подобных процессов. Есть два исключения. В адиабатном процессе вообще не происходит передачи тепла. Медленно сжимая поршнем газ в теплоизолированном сосуде, мы совершаем работу, нагревая при этом газ. Если отпустить поршень, то газ адиабатно расширится, охладившись до прежней температуры и совершив то же количество работы за счет своей внутренней энергии. Мы имеем дело с обратимым процессом. Другой обратимый процесс — это передача тепла от одного тела к другому при одинаковой температуре тел. Тогда тоже нет выделенного направления переноса тепловой энергии, и такой (изотермический) процесс также будет обратим, он должен происходить бесконечно медленно и поэтому будет равновесным. Таким образом, обратимыми могут быть адиабатный и изотермический процессы и любой цикл, построенный из таких процессов. С одним из них — циклом Карно — мы уже знакомы.
Но если тепло переносится при разных температурах контактирующих тел и тем более, если в системе есть трение или иные потери энергии, если в газе возникают ударные волны, вихри, турбулентности и т. п., то процесс будет неравновесным и необратимым. Так, взрыв паров бензина в цилиндре автомобильного двигателя не является обратимым процессом: движение поршня в обратном направлении никогда не приводит к рекомбинации продуктов взрыва обратно в пары бензина.
Следствием второго начала термодинамики является утверждение:
|
Все реальные процессы являются неравновесными и необратимыми.
|
В классической механике и электродинамике мы привыкли к тому, что невозможность какого-то процесса, как правило, связана с каким-то законом сохранения (энергии, импульса, электрического заряда и т. п.). Почему же невозможен вечный двигатель второго рода? Казалось бы, он не нарушает никаких законов сохранения? Чтобы понять это, надо обратиться еще к одной функции состояния системы — к энтропии.
Путь к этой новой для нас функции состояния недолог: надо взять уравнение первого начала термодинамики
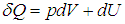
и разделить его обе части на температуру. Прежде всего учтем, что
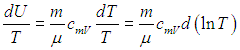
Далее в формуле для элементарной работы
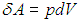
выразим объем через давление и температуру из уравнения состояния (1.7 ) идеального газа:
) идеального газа:
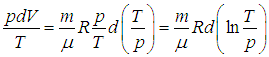
Получим в итоге с использованием соотношения Майера между молярными теплоемкостями
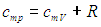
следующее выражение
|
|
|
(5.17) |
Правая часть (5.34) представляет собой дифференциал некоторой функции S состояния системы:
|
|
|
(5.18) |
где S0 — постоянная интегрирования, не зависящая от термодинамических параметров системы (давления, объема, температуры). Эта функция S называется энтропией. Получилось так, что величина dQ, не являющаяся дифференциалом какой-либо функции состояния, при делении на T стала таковым:
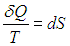
При замкнутом обратимом цикле изменение любой функции состояния (в частности, энтропии) равно нулю:
|
|
|
(5.19) |
Кружок на знаке интеграла означает, что интегрирование ведется по замкнутому контуру.
Проверим выполнение (5.19) на примере цикла Карно. Поскольку в этом цикле тепло получается системой и отдается только на изотермах (Т1,2 = const), температуру можно вынести из-под знака интеграла, и тогда интегрирование даст просто количество теплоты, поделенное на температуру, при которой оно получается или отдается. И действительно, выше было найдено, что на изотермических ветвях цикла при температуре Т1 газ получает теплоту
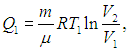
а при температуре Т2 — отдает теплоту
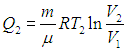
Выполнение равенства
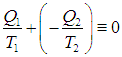
теперь очевидно. Напомним, что получаемое тепло имеет положительный знак, а отдаваемое — отрицательный; мы же определили ранее Q2 как абсолютную величину отдаваемого тепла, поэтому в формуле появился знак «–».
Проделаем теперь похожие выкладки с произвольным обратимым циклом. Выделим в нем две части: знаком «+» обозначим те фазы процесса, когда система получает тепло, а знаком «–» фазы, когда система отдает тепло. Поскольку полный интеграл равен нулю, аналогичные интегралы по двум частям цикла равны между собой:
|
|
|
(5.20) |
Если обозначить через Т1 максимальную температуру в первой части цикла, то неравенство Т < Т1 влечет за собой неравенство
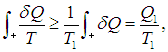
где Q1 как и прежде означает полное количество теплоты, полученное системой. Если ввести минимальную температуру Т2 во второй части цикла, то из Т > Т2 следует
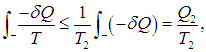
где Q2 — количество теплоты, отданное системой. Из этих неравенств и соотношения (5.20) следует, что
|
|
|
(5.21) |
Наконец получаем неравенство для КПД цикла
|
|
|
(5.22) |
С помощью понятия энтропии мы получили иным путем тот же результат: КПД любого цикла не превышает КПД цикла Карно с температурой нагревателя равной максимальной температуре рабочего тела и с температурой холодильника равной минимальной температуре рабочего тела рассматриваемого цикла. В дальнейшем мы будем опускать указание на то, что сравниваются КПД тепловых машин, работающих в одном и том же интервале температур.
Таким образом, мы убедились, что новая функция состояния — энтропия — связана со вторым началом термодинамики. До сих пор мы ограничивались равновесными (обратимыми) процессами. Рассмотрим пример неравновесного процесса. Пусть в начальном состоянии имеются два одинаковых идеальных газа с равными массами m при одинаковой температуре Т, но разных давлениях р1 и р2. Определим изменение энтропии 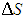 при соединении сосудов с газом.
при соединении сосудов с газом.
В первый момент после соединения сосудов, когда газы еще не смешались, энтропия системы равна сумме энтропии газов в отдельных сосудах:
|
|
|
(5.23) |
Найдем теперь объемы сосудов:
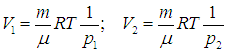
После соединения сосудов масса газа становится равной 2m, а объем — V = V1 + V2. Значит, давление р после соединения сосудов равно
|
|
|
(5.24) |
Поэтому энтропия газа после соединения сосудов равна
|
|
|
(5.25) |
Приращение энтропии 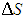 находится из (5.23) и (5.25):
находится из (5.23) и (5.25):
|
|
|
(5.26) |
Под знаком логарифма стоит величина, всегда большая единицы. Стало быть, энтропия увеличилась: 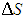 > 0.
> 0.
Цель этого примера, прежде всего, состоит в том, чтобы на частном случае продемонстрировать, как работает закон возрастания энтропии:
|
Если замкнутая система в некоторый момент времени находится в неравновесном состоянии, то процессы, протекающие в ней, приводят к возрастанию энтропии, которая достигает максимума, когда система приходит в равновесие. |
После того как мы соединили сосуды и, тем самым, открыли возможность перемешивания газов, мы получили неравновесное состояние с энтропией, равной сумме энтропий, газы стали перемешиваться, давления выравниваться, система перешла в равновесное состояние с большей, чем ранее энтропией. В результате перехода (благодаря внутренним процессам в системе) из первоначально неравновесного состояния в конечное равновесное состояние энтропия системы возрастает.
Закон возрастания энтропии является иной формулировкой второго начала термодинамики. Как мы сейчас убедимся, его смысл сводится к тому, что система стремится к более вероятному состоянию. Вспомним задачу о смешивании газов с разными давлениями. Вообще говоря, можно представить себе обратный процесс: газ и сосуде самопроизвольно разделится на две части, так что давления в каждой из частей будут различаться. Никакой закон сохранения не противоречит такому процессу, но он никогда не происходит в реальности, поскольку вероятность его ничтожно мала. Закон возрастания энтропии связан с тем, что данное макроскопическое состояние системы (определяемое параметрами Т, р, V) может быть реализовано множеством способов при различных микроскопических состояниях (определяемых положениями и скоростями молекул). Понятно ведь, что можно поменять импульсы пли положения какой-то пары молекул, и мы получим другое микроскопическое состояние, но термодинамически система не изменится. Число микроскопических состояний, соответствующих некоторому макроскопическому состоянию, определяет вероятность последнего: чем большим числом способов можно его реализовать, тем оно вероятнее. Возрастание энтропии, как уже говорилось, означает лишь то, что система стремится перейти в более вероятное состояние, которое реализуется большим числом микроскопических состояний.
Чтобы убедиться, что энтропия действительно связана с вероятностью, рассмотрим еще один неравновесный процесс. Пусть имеется сосуд объемом V, разделенный на правую и левую половины непроницаемой перегородкой. Пусть идеальный газ из N молекул содержится в левой половине сосуда, в то время как правая половина от молекул свободна. Перегородку делают проницаемой, так что газ может адиабатно расширяться в пустоту, как в эффекте Джоуля — Томсона. Определим изменение энтропии газа. Поскольку при расширении в пустоту не совершается работы против внешней силы, а тепла извне не поступает в силу условия адиабатности, идеальный газ не изменяет свою температуру. Увеличение же в два раза объема, занимаемого молекулами газа, приводит к двукратному уменьшению его давления от начального значения р1 до конечного р2 = р1/2. Поэтому энтропии газа до и после расширения равны, соответственно:
|
|
|
(5.28) |
а приращение энтропии дается выражением
|
|
|
(5.29) |
Каково же происхождение фактора 2N под знаком логарифма? Проследим за какой-нибудь молекулой. При непроницаемой перегородке она могла находиться только в левой половине сосуда, а потом ей стали доступны обе половины. Число способов размещения данной молекулы увеличилось в два раза, и так - для каждой из N молекул. Поэтому полное число способов размещения молекул увеличилось в 2N раз. В такое же число раз вероятность состояния газа, равномерно занимающего полный объем сосуда, больше вероятности состояния, когда при проницаемой перегородке все молекулы сосредоточатся в левой половине, оставив правую свободной. Это не противоречит никаким законам сохранения, но при N = NA = 6,02·1023 молекул (один моль вещества) вероятность такого события фантастически, грандиозно, невероятно мала 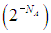 .
.
Еще один пример на ту же тему. Возьмем тот же сосуд, и пусть в каждой из его половинок находится равное число N/2 молекул при одинаковых температуре и давлении. Мысленно пометим молекулы левой половины черным цветом, а правой - белым, и пусть молекулы слева и справа больше ничем не отличаются. После этого соединим сосуды и определим приращение энтропии 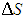 . После перемешивания температуры газов не изменятся, а их парциальные давления уменьшатся в два раза, так что полное давление, равное сумме парциальных, останется прежним. Поэтому процесс перемешивания сродни расширению газов черных и белых молекул в пустоту, и мы можем воспользоваться результатом (5.29), учитывая, что число молекул каждого цвета равно теперь N/2. Складывая затем приращения энтропий обоих газов, получаем
. После перемешивания температуры газов не изменятся, а их парциальные давления уменьшатся в два раза, так что полное давление, равное сумме парциальных, останется прежним. Поэтому процесс перемешивания сродни расширению газов черных и белых молекул в пустоту, и мы можем воспользоваться результатом (5.29), учитывая, что число молекул каждого цвета равно теперь N/2. Складывая затем приращения энтропий обоих газов, получаем
|
|
|
(5.30) |
(N пробегает теперь только четные значения). Убедимся, что и в данном случае 2N описывает увеличение числа способов распределения молекул по сосуду.
Рассмотрим рис. 5.7. Пусть у нас есть всего по одной молекуле в каждом из сосудов (N = 2). Раньше желтая молекула могла находиться только в левом сосуде, а после смешивания для нее стали доступны обе части соединенного сосуда. Аналогично расширились возможности для голубой молекулы, которая ранее была ограничена в своих передвижениях правым сосудом.
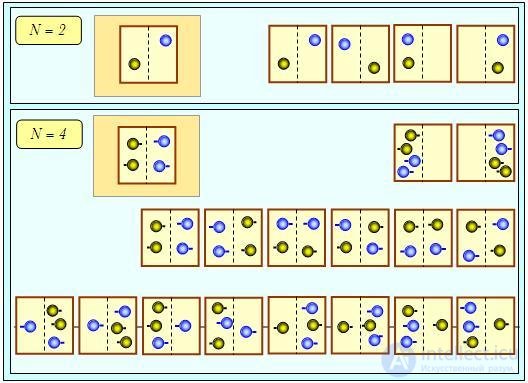
Рис. 5.7. Возрастание энтропии при смешивании одинаковых порций газа: при подсчете различных способов распределения молекул по частям соединенного сосуда надо различать каждую желтую и каждую голубую молекулу, для чего они снабжены «хвостиками», торчащими налево либо направо
Итак, после смешивания молекулы свободно блуждают по сосудам и мы имеем в четыре (22) раза больше вариантов их размещения (см. верхнюю часть рис. 5.7). Если у нас имеется N = 4 молекулы, то после соединения у них появляется в 24 = 16 больше возможностей распределиться по объему системы (нижняя часть рисунка). Ясно, что в общем случае N молекул число 2N действительно есть не что иное, как фактор, в который возрастает число способов распределения молекул по объему системы.
Можно дать статистическое определение энтропии:
|
|
|
(5.31) |
где W — число микроскопических способов, которыми можно реализовать данное макроскопическое состояние. Расчет вероятности макроскопических состояний и подстановка их в эту формулу приводит к прежним выражениям для энтропии идеального газа. Использование логарифма в определении энтропии позволяет свести умножение вероятностей к сложению энтропий. В наших примерах энтропия, приходящаяся на одну молекулу, возросла на величину
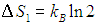
Двойка под логарифмом — это увеличение в два раза свободного пространства, доступного молекуле. Энтропия идеального газа из N молекул в N раз больше:
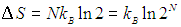
В классической статистике энтропия определяется с точностью до аддитивной постоянной S0. В квантовой статистике, оперирующей дискретными уровнями энергии, эта постоянная может быть определена. Оттуда, в частности, следует теорема Нернста (рис. 5.8), иногда называемая третьим началом термодинамики:

Рис. 5.8. Вальтер Герман Фридрих Нернст
|
При стремлении температуры к абсолютному нулю энтропия также стремится к нулю. |
Действительно, при абсолютном нуле температуры всякое тепловое движение прекращается и все молекулы находятся в состоянии с низшей энергией. Поэтому есть только один способ реализации такого состояния (W = 1), так что S = 0. (Это неверно для систем, у которых имеется несколько низших энергетических состояний).
Представим себе, что мы снимаем фильм о смешивании молекул в сосудах. Сначала у нас слева — желтые молекулы, а справа — голубые. Молекулы сталкиваются, путешествуют по сосудам и в конечном итоге равномерно перемешиваются (так сказать, их смесь дает более или менее ровный зеленый цвет). Такое поведение системы большого числа частиц соответствует нашей практике. Запустим теперь фильм в обратном направлении. В каждом отдельном кадре, то есть в конкретном акте соударения молекул, мы не увидим ничего особенного. Законы механики не нарушатся на нашем экране, поскольку они обратимы. Но конечный итог «обратного» фильма поистине чудесен: казалось бы, беспорядочные столкновения молекул привели к разделению зеленого цвета на желтый слева и голубой справа. В таком процессе энтропия уменьшается, а система приходит от беспорядка к порядку. На самом деле каждая молекула имела в точности такие скорости и положения, испытывала именно такие, а не другие столкновения, чтобы в конце концов прийти в ту половину сосуда, где она оказалась. Такое событие в высшей степени невероятно, хотя и не противоречит микроскопическим законам физики. Закон возрастания энтропии утверждает, что система с течением времени имеет тенденцию перейти в менее упорядоченное состояние. Как говорится, «энтропия возрастает, а мир стремится к хаосу». Вопрос же о самоорганизации материи, о возникновении порядка из хаоса — предмет совсем другой науки, синергетики.
|
тепловой двигатель — это периодически действующее устройство, в котором тепловая энергия преобразуется в механическую работу. |
Тепловые двигатели разнообразны по конструкции и назначению. К ним относятся паровые машины, двигатели внутреннего сгорания, реактивные двигатели и т. д. (см. рис. 5.9).
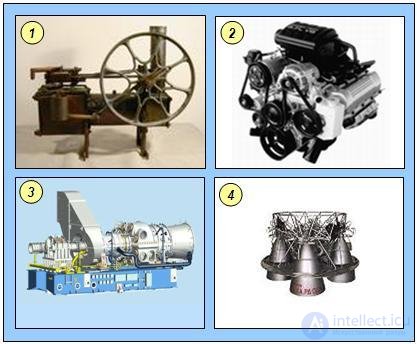
Рис. 5.9. Тепловые двигатели: 1 — паровая машина; 2 — двигатель внутреннего сгорания; 3 — газовая турбина; 4 — ракетный двигатель
Несмотря на многообразие, в основе практически всех тепловых двигателей лежит общий принцип — принцип циклического действия. Основными частями любого теплового двигателя являются: нагреватель, рабочее тело и холодильник.
Рассмотрим в качестве примера работу четырехтактного двигателя внутреннего сгорания. В этом двигателе высокая температура достигается за счет сгорания рабочей смеси (бензина с воздухом) внутри цилиндра двигателя; воспламенение смеси происходит с помощью искрового зажигания. Перечислим основные стадии работы четырехтактного двигателя внутреннего сгорания:
Работа четырехтактного двигателя внутреннего сгорания показана на рис. 5.10.
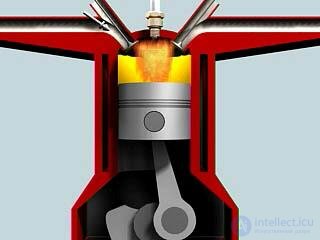
Рис. 5.10. Работа четырехтактного двигателя внутреннего сгорания
Рассмотрим идеализированный процесс (цикл Отто), близкий к используемому в четырехтактном двигателе внутреннего сгорания. Цикл Отто изображен на рис. 5.11.
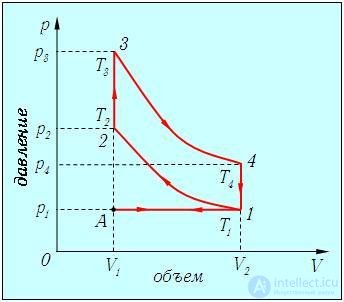
Рис. 5.11. Идеализированный цикл четырехтактного двигателя внутреннего сгорания (цикл Отто)
Как обычно, термодинамические параметры имеют индексом номер соответствующей точки на рисунке (в данном случае надо будет помнить, что V3 = V2; V4 = V1).
Изобара А-1. Первый такт цикла. Вследствие движения поршня в цилиндр всасывается горючее. Приближенно можно считать, что это происходит при атмосферном давлении p1. Объем увеличивается от V1 до V2.
Адиабата 1-2. Второй такт цикла. Теплообмена со средой нет. Поршень движется в обратном направлении, адиабатно сжимая смесь от объема V1 до объема V2. При этом повышается давление, и температура растет от Т1 до Т2. Связь температур и объемов в начале и конце адиабатной части цикла дается соотношением
|
|
|
(1) |
Изохора 2-3. Начало третьего такта. Под действием электрической искры горючая смесь взрывается: давление почти мгновенно возрастает до значения р3, а объем еще не успевает измениться. Температура растет от T2 до Т3 за счет тепла, выделенного при взрыве. Работа не производится, а количество полученного тепла выражается формулой
|
|
|
(2) |
Адиабата 3-4. Продолжение третьего такта. Теплообмена со средой нет. Газ адиабатно расширяется до максимального объема цилиндра V1, падают температура и давление. Связь температур и объемов в начале и конце адиабаты дается уравнением
|
|
|
(3) |
Изохора 4-l. Конец третьего такта. Открывается клапан, давление падает до атмосферного при постоянном объеме. Температура также падает до значения Т1.
|
|
|
(4) |
Изобара 1-А. Четвертый такт. Поршень выталкивает из цилиндра отработанные газы, система возвращается в начальное состояние. Поскольку участок А-1 проходится дважды в разных направлениях, соответствующие вклады в работу и в теплоту сокращаются и могут не приниматься во внимание.
Таким образом, получаем для КПД цикла
|
|
|
(5) |
Из уравнений (1), (3) следует равенство отношений
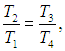
откуда находим
|
|
|
(6) |
Подставляя (6) в (5), приходим к окончательному выражению для КПД цикла
|
|
|
(7) |
Оно получилось очень похожим на формулу для КПД цикла Карно, но обратим внимание, что максимальной температурой здесь является температура в точке 3 (Тmах = Т3), а минимальной - температура в точке 1 (Tmin = T1). Поэтому КПД цикла Карно, работающего между такими температурами, равнялся бы
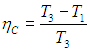
Разность этих двух выражений отлична от нуля:
|
|
|
(8) |
поскольку Т4 > T1. Мы воочию убедились, что КПД рассмотренного цикла меньше КПД цикла Карно. Заметим также, что КПД цикла Отто можно выразить через отношение объемов:
|
|
|
(9) |
Величина V1/V2 называется сжатием. Получается, что КПД рассмотренного цикла определяется только величиной сжатия горючей смеси и показателем адиабаты.
Помимо цикла Карно и технических циклов, используемых в различных двигателях, представляет интерес так называемая внутреннеобратимая тепловая машина (смысл названия станет ясен позже). Дело в том, что максимальный КПД, соответствующий циклу Карно, никогда не достигается на практике. Более того, если бы это было даже возможно, далеко не очевидно, что такую машину стоило бы создавать. Помимо КПД в реальной жизни немаловажную роль играют также простота устройства и управления, стоимость установки, ее надежность, скорость работы и тому подобные требования, которые зачастую конфликтуют между собой. В цикле Карно контакты рабочего тела с тепловыми резервуарами происходят при одинаковой температуре. Это значит, что тепло перетекает бесконечно медленно, что, конечно, очень непрактично. Представление о реальной производительности используемых установок можно получить, рассматривая внутреннеобратимую тепловую машину.
Предположим снова, что мы имеем два тепловых резервуара при температурах Тmaх и Tmin. Предположим также, что работа производится циклом Карно, функционирующим при температурах нагревателя T1 и холодильника Т2. Имеется в виду, что выполняется следующая цепочка неравенств: Tmах > T1 > Т2 > Tmin. Иными словами, мы рассматриваем необратимый в целом процесс, внутри которого есть обратимый цикл. Тепло подается к рабочему телу при постоянной разности температур Тmах – T1 и отводится от него при постоянной разности температур Т2 – Тmin (см. схему на рис. 5.13).
Рис. 5.13. Цикл внутреннеобратимой тепловой машины, имитирующий реальные энергетические установки
В этом и заключается главное отличие от стандартного идеального цикла Карно, где соответствующие разности температур равны нулю.
Предположим, что скорость теплообмена между рабочим телом и тепловыми резервуарами пропорциональна разности температур между ними:
|
|
|
(1) |
где Q+, t+ — получаемое количество теплоты и время его передачи рабочему телу при контакте с нагревателем, a Q-, t– — количество теплоты, отдаваемой холодильнику, и время этого процесса. Величины с+ и с– — соответствующие коэффициенты теплопередачи. Тогда полное время t теплообмена равно
|
|
|
(2) |
Время, затрачиваемое машиной на внутренний цикл Карно, определяется временем установления равновесия в рабочем теле, которое существенно меньше, чем время передачи тепла t. Поэтому t можно считать временем совершения полного цикла.
Как обычно, мы предполагаем, что отсутствуют потери тепла на трение и тому подобные процессы. Количества теплоты Q+ и Q–, а также совершенная работа А связаны между собой соотношениями, найденными нами при изучении цикла Карно:
|
|
|
(3) |
Подставляя (3) в (2), находим для времени осуществления цикла выражение
|
|
|
(4) |
Мощность рассматриваемой машины равна A/t. Представим себе, что мы проектируем такую машину. У нас имеется возможность выбрать оптимальным образом температуры Т1, Т2, при которых функционирует внутренний цикл Карно. Выбирая их равными Тmах и Тmin соответственно, мы добьемся максимального КПД. Но из формулы (4) следует, что при этом
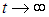
и выходная мощность машины стремится к нулю. Более практично выбрать температуры таким образом, чтобы максимума достигла выходная мощность. Приравнивая нулю производные по Т1 и Т2 от выражения (4) для t/A, находим уравнения для этих температур. Опуская детали, приведем лишь конечный результат: максимальная выходная мощность при этих условиях равна
|
|
|
(5) |
Достигается это значение при температурах внутреннего цикла Карно
|
|
|
(6) |
где параметр Т0, имеющий смысл некой средней температуры системы, определен соотношением
|
|
|
(7) |
Очевидно, что КПД нашей машины равен КПД внутреннего цикла Карно
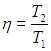
Поскольку отношение температур внутреннего цикла равно квадратному корню из отношения температур нагревателя и холодильника, находим КПД внутреннеобратимой машины:
|
|
|
(8) |
Легко убедиться, что КПД меньше максимально возможного
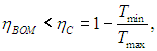
но зато мы выиграли в выходной мощности. Любопытно, что КПД оптимизированной по мощности внутреннеобратимой машины не зависит от коэффициентов с+ и с–: как и в цикле Карно, он определяется лишь отношением температур нагревателя и холодильника. Авторы концепции внутреннеобратимой машины (F.L. Curzon and В. Ahlborn, Amer. J. Phys. 43, 22, 1975) приводят следующую таблицу, где сравниваются несколько крупных электростанций. Видно, что формула (8) гораздо лучше соответствует практике, нежели КПД идеального цикла Карно.
Таблица
Сравнение наблюдаемых КПД нескольких электростанций разных типов с КПД цикла Карно hС и цикла внутреннеобратимой машины hВОМ
|
Местонахождение и тип электростанции |
Тmin, °С |
Tmax, °С |
hС |
hВОМ |
Наблюдаемый КПД |
|
West Thurrock, Великобритания (угольная) |
25 |
565 |
0,64 |
0,40 |
0,36 |
|
CANDU, Канада (ядерная) |
25 |
300 |
0,48 |
0,28 |
0,30 |
|
Larderello, Италия (геотермальная) |
80 |
250 |
0,33 |
0,18 |
0,16 |
В заключение этого параграфа приведем численный пример.
Пример. Пусть коэффициенты теплопередачи с+ одинаковы и таковы, что при разнице температур DТ = 10 К мощность теплового потока между тепловыми резервуарами и рабочим телом составляет 1 кВт. Иными словами,
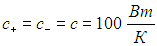
Пусть далее температуры резервуаров составляют Тmах = 50 °С = 823 К и Тmin = 20 °С = 293 К. Найдем максимальную выходную мощность внутреннеобратимой тепловой машины и температуры T1 и Т2, при которых должно функционировать рабочее тело, использующее цикл Карно.
Из формулы (5.29) следует, что при равенстве коэффициентов теплопроводности «средняя» температура Т0 определяется как
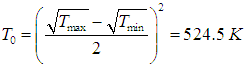
Используя соотношения (5.28), находим оптимальные температуры
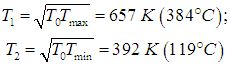
КПД такой установки равен hBOM = 0,403 (ср. hС = 0,644). При таким образом выбранных температурах рабочего тела достигается максимальная выходная мощность, определяемая по формуле (5):
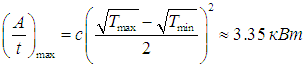
Исследование, описанное в статье про второе начало термодинамики, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое второе начало термодинамики, кпд тепловых машин, цикл карно, двигатель внутреннего сгорания, двс, тепловой двигатель и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Молекулярная физика и термодинамика
Комментарии
Оставить комментарий
Молекулярная физика и термодинамика
Термины: Молекулярная физика и термодинамика