П.1.4. Законы распределения случайных величин, используемые в математических моделях.

Привет, Вы узнаете о том , что такое законы распределения случайных величин, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое законы распределения случайных величин, случайные величины , настоятельно рекомендую прочитать все из категории Основы сотовой связи стандарта GSM.

Характерными для систем сотовой мобильной связи является многократное отражение, рас­сеяние, поглощение радиоволн и отсутствие детерминированных закономерностей, наблю­даемых для условий прямой видимости между базовой и мобильной станциями. В точке приема (как в случае BTS, так и MS) результирующее значение вектора напряженности по­ля определяется как геометрическая сумма множества векторов (многолучевое распростра­нение радиоволн), амплитуды и фазы которых изменяются по случайным законам.
Кроме этого, сотовое построение сети приводит к взаимным влияниям излучателей, имеющих равные несущие частоты (соканальные помехи), а также шумы приводят к допол­нительному изменению условий надежного приема информации.
Поэтому, чтобы оценить качество радиосвязи в системе сотовой мобильной связи, необ­ходимо использовать вероятностные характеристики.
Особенно важными для построения математических моделей радиоканалов являются за­коны распределения случайных величин. В теории передачи информации со статистически изменяющимися параметрами каналов используются следующие законы распределения:

- распределение Релея (для описания быстрых затуханий);
- распределение Гаусса (используемое для описания шумов и помех от случайных ис­точников сигнала);
- нормальное логарифмическое (или лог-нормальное) распределение (используемое для описания медленных затуханий);
- распределение Райсса-Накагами (используемое для описания распространения ра­диоволн в средах при диффузном рассеянии на случайных неоднородностях).
Распределение Релея
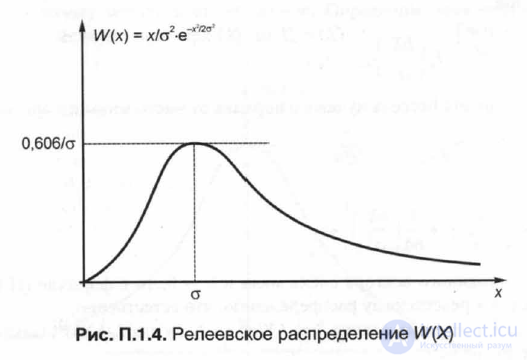
Распространение радиосигналов в средах с замираниями (точнее в средах, где возникают процессы диффузной многолучевости поля и в месте приема поле представляет собой ре­зультат интерференции бесконечно большого числа элементарных лучей) может быть опи­сано релеевской функцией плотности распределения вероятностей вида:

где X— случайная величина; а2 = А — дисперсия, случайной величины; при этом величина Xможет принимать многие значения в интервале от 0 до оо, то есть:

На рис. П. 1.4 показано релеевское распределение W(X).Приравнивая производную к нулю dW/dX= 0, определим наивероятное значение Хндля релеевского закона: Хн= а, при этом W(X=а) = 0,606/а.


Среднее значение (математическое ожидание) в случае релеевского распределения оп­ределяется по формуле:

(П.1.20)
Закон Релея дает статистическое описание изменений длины результирующего вектора при геометрическом сложении достаточно большого числа векторов со случайно изменяющи­мися амплитудами (модулями) при статистической независимости амплитуд и фаз и равно­мерном распределении фазы. Для оценки близости распределений к релеевскому закону часто пользуются отношением значений X,соответствующим вероятностям 0,9 и 0,1. Из формулы (П. 1.19) можно определить, что это отношение равно 4,66, что соответствует 13,37 дБ.
Завершая рассмотрение распределения Релея, следует отметить, что под случайной ве­личиной Xпонималась случайная величина напряженности поля радиоволны (либо Е,либо Я). Об этом говорит сайт https://intellect.icu . Поэтому в разделах, посвященных рассмотрению релеевской модели многолучевого распространения радиоволн в системах мобильной связи, вместо X,необходимо подстав­лять Е(или Н).

Обобщенный закон распределения Релея
Если закон описывает распределение длины результирующего вектора при геометриче­ском сложении векторов с постоянной длиной волны и неизменной фазой и суммы слу­чайных векторов, распределенных по закону Релея, такой закон распределения называют обобщенным законом распределения Релея. Плотность распределения для этого закона вы­ражается формулой:

Если длина постоянного вектора очень мала и 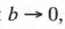то в формуле (П. 1.21) получится предельный переход к релеевскому распределению, что естественно.
Если величина Ънастолько велика, что 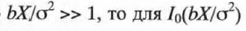можно использовать асимптотическое значение:

Закон распределения Гаусса (нормальный закон распределения)

Гауссовская функция плотности распределения вероятностей — функция, используемая для описания шума и источников случайных сигналов.
Гауссовская функция плотности вероятностей определяется по формуле:

где X— случайная величина, (X)— среднее значение, о— среднеквадратическое отклоне­ние. На рис. П. 1.5 показана гауссовская функция W(X).
Как следует из рисунка, функция W(X)симметрична относительно (X)среднего значе­ния, а величина Xможет меняться от -оо до + оо. Определим наивероятное значение Хн: так как dW/dX=0 существует лишь при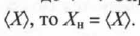

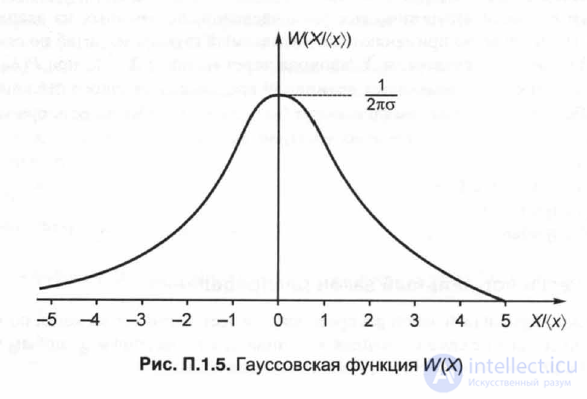
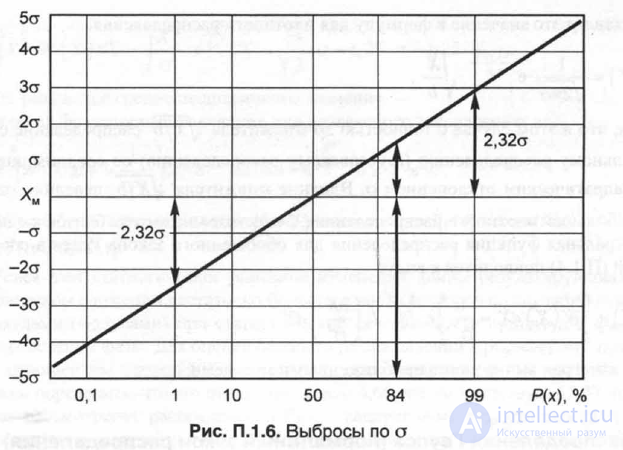
Рис. П.1.6. Выбросы по о Интегральная функция распределения для гауссовского закона определяется из формулы:

где erf(Z) — интеграл вероятности (табулированный), функция ошибок.
Если X= -(X),то Р((Х))= 0,5, то есть для гауссовского закона медианное значение слу­чайной величины Хм= (X)= Хи.
Для оценки близости статистических распределений, полученных из эксперимента, к гауссовскому закону обычно применяют так называемый гауссов масштаб по оси вероятно­сти, в нем Р(Х)линейно меняется от X,проходя через медиану X = Хмпри Р(ХМ)= 0,5, при этом наклон этой прямой определяется величиной среднеквадратичного отклонения о.Как отмечено в работе [П. 1.1], выбросы по а могут быть до ±4а и ±5а, то есть при гауссовском распределении изменение Р(Х)в пределах ±5а (рис. П. 1.6):

Логарифмически нормальный закон распределения

Логарифмически нормальный закон распределения имеет место тогда, когда по нормально­му закону распределена не сама случайная величина X,а ее логарифм (с любым в принципе основанием). Если взять основание 10, и ввести обозначения:

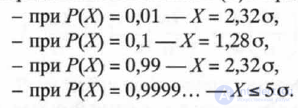
Из данной формулы следует, что она справедлива не только для логарифма случайной величины, но и произведения этого логарифма на любую постоянную величину. Поэтому логарифмически нормальный закон соответствует нормальному закону распределения слу­чайной величины, выраженной в децибелах.
Числовые характеристики такого распределения: (X) =(Xm)l, oLтакже выражаются в де­цибелах относительно выбранного уровня.
Для оценки близости распределений, найденных из эксперимента, к логарифмически нормальному закону можно воспользоваться гауссовским масштабом по оси абсцисс, а по оси ординат наносить в равномерном масштабе значения случайной величины в децибелах.
Например при P(XL)= 0,99, XL=2,32 aL, дБ.

Распределение Райсса-Накагами

При рассмотрении диффузно рассеянного электромагнитного поля Ена неоднородностях типа лесных массивов, то есть вне зеркальных направлений, среднее значение напряженно­сти поля в этом случае (Е)=>0, а само поле Есостоит из полей, рассеянных различными участками неоднородностей [П. 1.2].
Если допустить, что поле в точке приема равно сумме квадратурных составляющих:

то значения составляющих Е\и Е2можно представить в виде суммы большого числа неза­висимых величин Еци E2hто есть:

В соответствии с центральной предельной теоремой распределение случайной величи­ны, представляющей собой сумму Nнезависимых случайных величин, при N-> оо прибли­жается к нормальному закону распределения независимо от того, какому распределению подчиняется каждое из слагаемых.
Если предположить, что каждое слагаемое в квадратурном представлении Е, то есть в формулах (П. 1.30) и (П. 1.31) составляющие являются независимыми случайными величина­ми, то в направлении, где поле складывается из когерентной (Е)и некогерентной состав­ляющих нужно исследовать выражение (П. 1.32).
Если допустить, что когерентное поле запишется в виде:

и отсчитывать фазу так, чтобы гр0 = 0, то некогерентное поле можно представить в виде раз­ности: 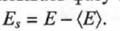(П. 1.34)
Учитывая формулу (П. 1.28), можно Esзаписать в виде большого числа слагаемых:

Используя центральную предельную теорему, функция плотности распределения веро­ятности запишется в виде:
(П.1.36)
где о]— дисперсия {Ex-Aq)и Е2.
Тогда плотность распределения вероятности амплитуды Аопределяется формулой Райсса-Накагами [П1.2]:
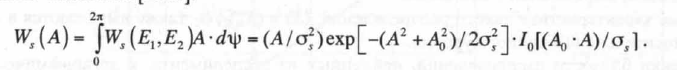(П.1.37)
Следует отметить, что для электромагнитных волн, рассеянных на лесных массивах (густо заросший лес), с учетом ветровых колебаний лесной растительности, распределение (П.1.3.7) при т2 <1 запишется в виде [П.1.4]:
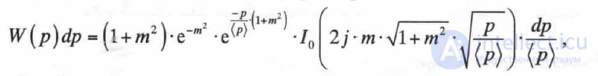(П. 1.38)
где 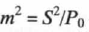— отношение мощности устойчивого сигнала к средней мощности сигнала от перемещения отражателей (ветрового перемещения), Р— случайная функция (в данном случае распределения амплитуды напряженности поля А), /0 — модифицированная функ­ция Бесселя нулевого порядка.
При 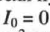это распределение переходит в релеевское.
При распределение (П.1.38) превращается в обычную показательную функцию:
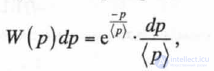П.1.39
которая выражает распределение поля, созданного рассеянием электромагнитных волн на конгломерате одних случайных отражателей.

Анализ данных, представленных в статье про законы распределения случайных величин, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое законы распределения случайных величин, случайные величины и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Основы сотовой связи стандарта GSM