Лекция
Привет, Вы узнаете о том , что такое однослойный персептрон, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое однослойный персептрон, решение задачи классификации , настоятельно рекомендую прочитать все из категории Нейронные сети.
Перцептро́н, или персептрон (англ. perceptron от лат. perceptio — восприятие; нем. perzeptron) —математическая или компьютерная модель восприятия информации мозгом (кибернетическая модель мозга), предложенная Фрэнком Розенблаттом в 1957 году и реализованная в виде электронной машины «Марк-1» в 1960 году. Перцептрон стал одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером. Несмотря на свою простоту, перцептрон способен обучаться и решать довольно сложные задачи. Основная математическая задача, с которой он справляется, — это линейное разделение любых нелинейных множеств, так называемое обеспечение линейной сепарабельности.
Перцептрон состоит из трех типов элементов, а именно: поступающие от сенсоров сигналы передаютсяассоциативным элементам, а затем реагирующим элементам. Таким образом, перцептроны позволяют создать набор «ассоциаций» между входными стимулами и необходимой реакцией на выходе. В биологическом плане это соответствует преобразованию, например, зрительной информации в физиологический ответ от двигательныхнейронов. Согласно современной терминологии, перцептроны могут быть классифицированы как искусственные нейронные сети:
На фоне роста популярности нейронных сетей в 1969 году вышла книга Марвина Минского и Сеймура Паперта, которая показала принципиальные ограничения перцептронов. Это привело к смещению интереса исследователей искусственного интеллекта в противоположную от нейросетей область символьных вычислений . Кроме того, из-за сложности математического анализа перцептронов, а также отсутствия общепринятой терминологии, возникли различные неточности и заблуждения.
Впоследствии интерес к нейросетям, и в частности, работам Розенблатта, возобновился. Так, например, сейчас стремительно развивается биокомпьютинг, который в своей теоретической основе вычислений, в том числе, базируется на нейронных сетях, а перцептрон воспроизводят на основе бактериородопсин-содержащих пленок.

Можно выделить два класса задач, решаемых обучаемыми нейронными сетями. Это задачи предсказания и классификации.
Задачи предсказания или прогнозирования являются, по существу, задачами построения регрессионной зависимости выходных данных от входных. Нейронные сети могут эффективно строить сильно нелинейные регрессионные зависимости. Специфика здесь такова, что, поскольку решаются в основном неформализованные задачи, то пользователя интересует в первую очередь не построение понятной и теоретически обоснованной зависимости, а получение устройства-предсказателя. Прогноз такого устройства непосредственно не пойдет в дело – пользователь будет оценивать выходной сигнал нейросети на основе своих знаний и формировать собственное экспертное заключение. Об этом говорит сайт https://intellect.icu . Исключения составляют ситуации, на основе обученной нейронной сети создают устройство управления для технической системы.
При решении задач классификации нейронная сеть строит разделяющую поверхность в признаковом пространстве, а решение о принадлежности ситуации тому или иному классу принимается самостоятельным, не зависящим от сети устройством – интерпретатором ответа сети. Наиболее простой интерпретатор возникает в задаче бинарной классификации (классификации на два класса). В этом случае достаточно одного выходного сигнала сети, а интерпретатор относит, например, ситуацию к первому классу, если выходной сигнал меньше нуля, и ко второму, если он больше или равен нулю.
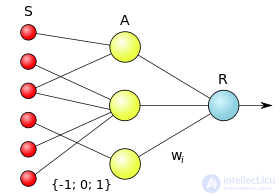
Структура и свойства искусственного нейрона
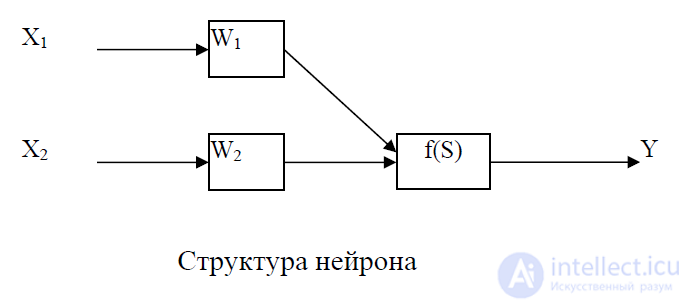
Нейрон является составной частью нейронной сети. На рис. 2 показана его структура. Он состоит из элементов трех типов: умножителей (синапсов), сумматора и нелинейного преобразователя. Синапсы осуществляют связь между нейронами, умножают входной сигнал на число, характеризующее силу связи, (вес синапса). Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента - выхода сумматора. Эта функция называется функцией активации или передаточной функцией нейрона.


Рис. 2. Структура искусственного нейрона
Нейрон в целом реализует скалярную функцию векторного аргумента. Математическая модель нейрона:
|
|
(1.1) |
|
|
y = f(s) |
|
(1.2) |
где w i, - вес (weight) синапса, i = 1...n; b - значение смещения (bias); s - результат суммирования (sum); x, - компонент входного вектора (входной сигнал), x i = 1... n ; у - выходной сигнал нейрона; n - число входов нейрона; f - нелинейное преобразование (функция активации).
В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения, а во многих практических задачах - лишь некоторые фиксированные значения. Выход (у) определяется видом функции активации и может быть как действительным, так и целым.
Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами - тормозящими.
Описанный вычислительный элемент можно считать упрощенной математической моделью биологических нейронов. Чтобы подчеркнуть различие нейронов биологических и искусственных, вторые иногда называют нейроноподобными элементами или формальными нейронами.
На входной сигнал (s) нелинейный преобразователь отвечает выходным сигналом f(s), который представляет собой выход у нейрона. Примеры активационных функций представлены в табл. 1. и на рис. 3.
Таблица 1
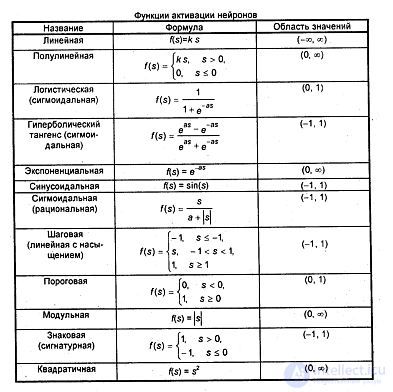

Рис. 3. Примеры активационных функций
а - функция единичного скачка; б - линейный порог (гистерезис);
в - сигмоид (логистическая функция); г - сигмоид (гиперболический тангенс)
Таблица 2 .основные варианты описания активационной функции

Одной из наиболее распространенных является нелинейная функция активации с насыщением, так называемая логистическая функция или сигмоид (функция S-образного вида):
|
f (s) = 1 / (1+e -as) |
(1.3) |
При уменьшении а сигмоид становится более пологим, в пределе при а = 0 вырождаясь в горизонтальную линию на уровне 0,5, при увеличении а сигмоид приближается к виду функции единичного скачка с порогом 0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне (0, 1). Одно из ценных свойств сигмоидальной функции - простое выражение для ее производной, применение которой будет рассмотрено в дальнейшем:
|
f ' (s) = a f(s)[ 1 -f(s)] |
(1.4) |
Следует отметить, что сигмоидальная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.
Формальный нейрон состоит из 3 логических блоков: входы, функция преобразования, выход. Рассмотрим подробнее блок функции преобразования.
Рисунок 4. Модель формального нейрона. Пунктирной рамкой выделен блок функции преобразования.
В качестве функции преобразование обычно используются следующие:

, 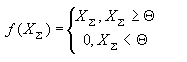
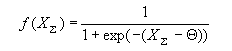
Примеры простейших задач
1. Вычислите сетевой выход персептрона с биполярной сигмоидальной активационной функцией,
если известны следующие параметры: x1=0.7; w1=1.5;x2=2.5; w2=-1; b=0.5.
2. Вычислите сетевой выход персептрона с униполярной сигмоидальной активационной функцией,
если известны следующие параметры: x1=0.7; w1=1.5;x2=2.5; w2=-1; b=0.5.
Решение простейшей абстрактной задачи
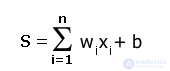
функция активации : y = F(s)
Значение функции активации вычисляем по формуле

k - принимаем любым числом
Выводы из данной статьи про однослойный персептрон указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое однослойный персептрон, решение задачи классификации и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Нейронные сети
Из статьи мы узнали кратко, но содержательно про однослойный персептрон
Комментарии
Оставить комментарий
Нейронные сети
Термины: Нейронные сети