5. Количественная оценка надежности программного обеспечения кратко

Привет, Вы узнаете о том , что такое количественная оценка надежности программного обеспечения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое количественная оценка надежности программного обеспечения , настоятельно рекомендую прочитать все из категории Надёжность программного обеспечения.

5.1. Характеристика качества ПО «Надежность» по стандарту ISO 9126

Международный стандарт  ISO/IEC 9126 определяет 6 основных характеристик качества программного обеспечения: функциональность, надежность, практичность, эффективность, сопровождаемость, переносимость. Для характеристики надежность определено 4 подхарактеристики: завершенность, отказоустойчивость, восстанавливаемость и согласованность надежности.

Метрики для подхарактеристик:

Метрики завершенности:
1.1. обнаружение неисправностей показывает, сколько ошибок было обнаружено при экспертизе продукта;

1.2. устранение неисправностей — показывает количество исправленных ошибок;

1.3. тестовая адекватность — показывает, насколько требуемые тестовые воздействия покрыты тестовым планом.

Метрики отказоустойчивости:
2.1. избежание неисправностей – показывает количество схем неисправностей, которые были сведены под управление для избежания чрезвычайных и критических неисправностей;

2.2. неверная операция избежания – количество функций, реализованных для избежания неверных схем операций.

Метрики восстанавливаемости:
3.1. восстанавливаемость – показывает, насколько продукт способен к восстановлению после непредусмотренного события или запроса;

3.2. эффективность восстановления – насколько эффективна способность к восстановлению.

Метрики соответствия надежности:
4.1. соответствие надежности – показывает, насколько продукт соответствует надежности к применимым положениям стандартов.

5.2. количественная оценка надежности программного обеспечения с использованием функция Харрингтона-Менчера

 

 

5.2. Количественная оценка надежности программного обеспечения с использованием функция Харрингтона-Менчера

 

Предпосылками для создания данной методики оценки явилось отсутствие удобного подхода для обработки вычисленных значений метрик. В ее основе лежат несколько концепций. Рассмотрим их по порядку.

Значение каждой метрики надежности (см. п. 5.1.) преобразуется в безразмерную шкалу желательности d, называемую также шкалой желательности Харрингтона. Таким образом, физический параметр, каковым является метрика, преобразуется в психологическую величину, представляющую собой числовое выражение эмпирической оценки данной метрики.

Оно отражает мнение наблюдателя (им является программист, аналитик, эксперт – в общем случае это некоторый человек, объектом рассмотрения которого является надежность данного программного продукта) и находится в интервале от нуля до единицы. Нулевое значение соответствует абсолютно неприемлемому уровню данного свойства, единичное – самому лучшему. Соотношение между значениями шкалы желательности в эмпирической и числовой (психологической) системами представлено в таблице 5.1.

 

Таблица 5.1. – Связь между количественными значениями безразмерной шкалы и психологическим восприятием человека

 

Желательность	Отметка на шкале желательности
Очень хорошо	1,00 – 0,80
Хорошо	0,80 – 0,63
Удовлетворительно	0,63 – 0,37
Плохо	0,37 – 0,20
Очень плохо	0,20 – 0,00

 

Выбор отметок на шкале желательности 0,63 и 0,37 продиктован удобством вычислений: 0,63~=  1-(1/е), 0,37~=1/е. Значение di=0,37 соответствует границе допустимых значений.

Такой подход предполагает выбор функции, задающей рассмотренное преобразование, – функции желательности. Об этом говорит сайт https://intellect.icu . Она может вычисляться по формуле

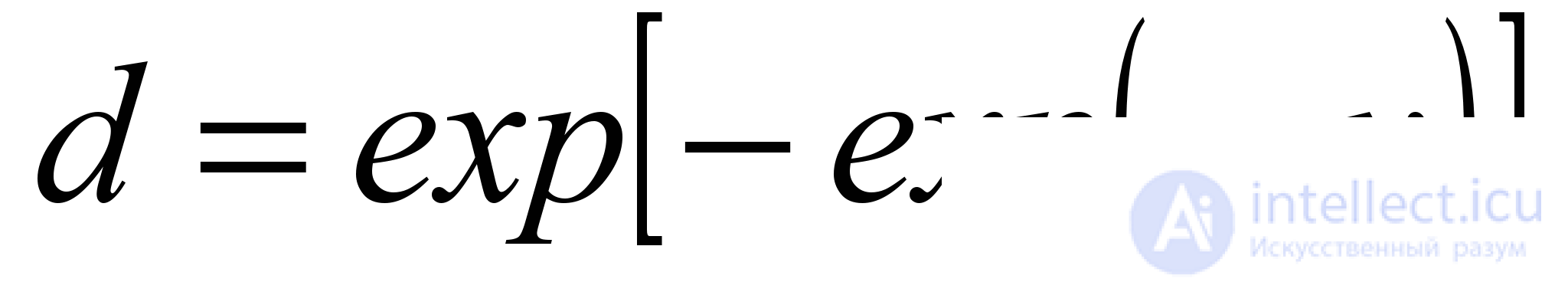, (5.1)

где d – значение на шкале желательности,

y – исходное значение метрики.

Для расчета количественной оценки надежности программного продукта будем использовать обобщенную функцию желательности Харрингтона-Менчера:

D =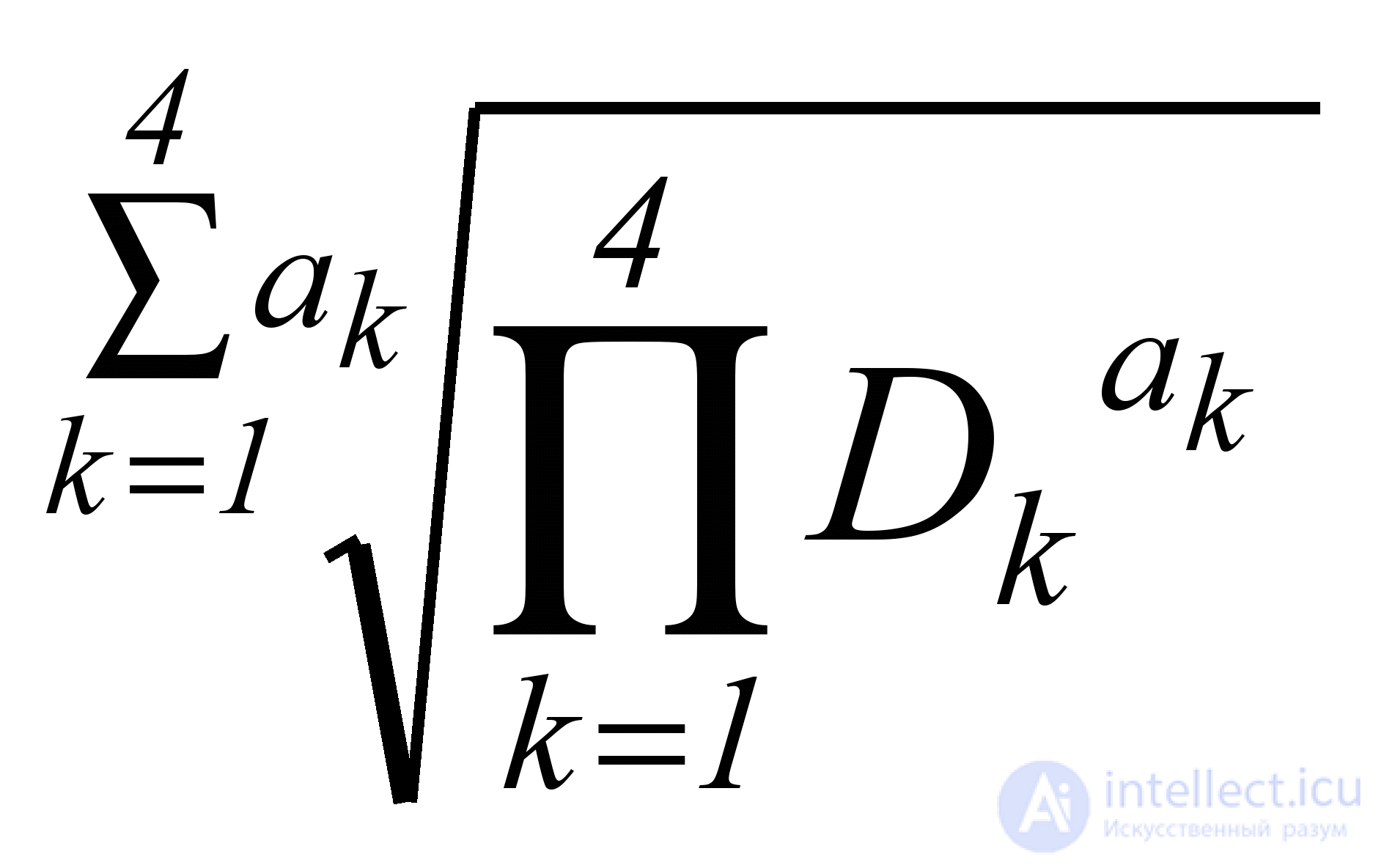, (5.2.)

где Dk – обобщенная функция желательности для k-ой подхарактеристики, имеющей вес аk;

4 – число подхарактеристик.

Каждая подхарактеристика надежности, в свою очередь, может быть представлена в виде функции:

Dk =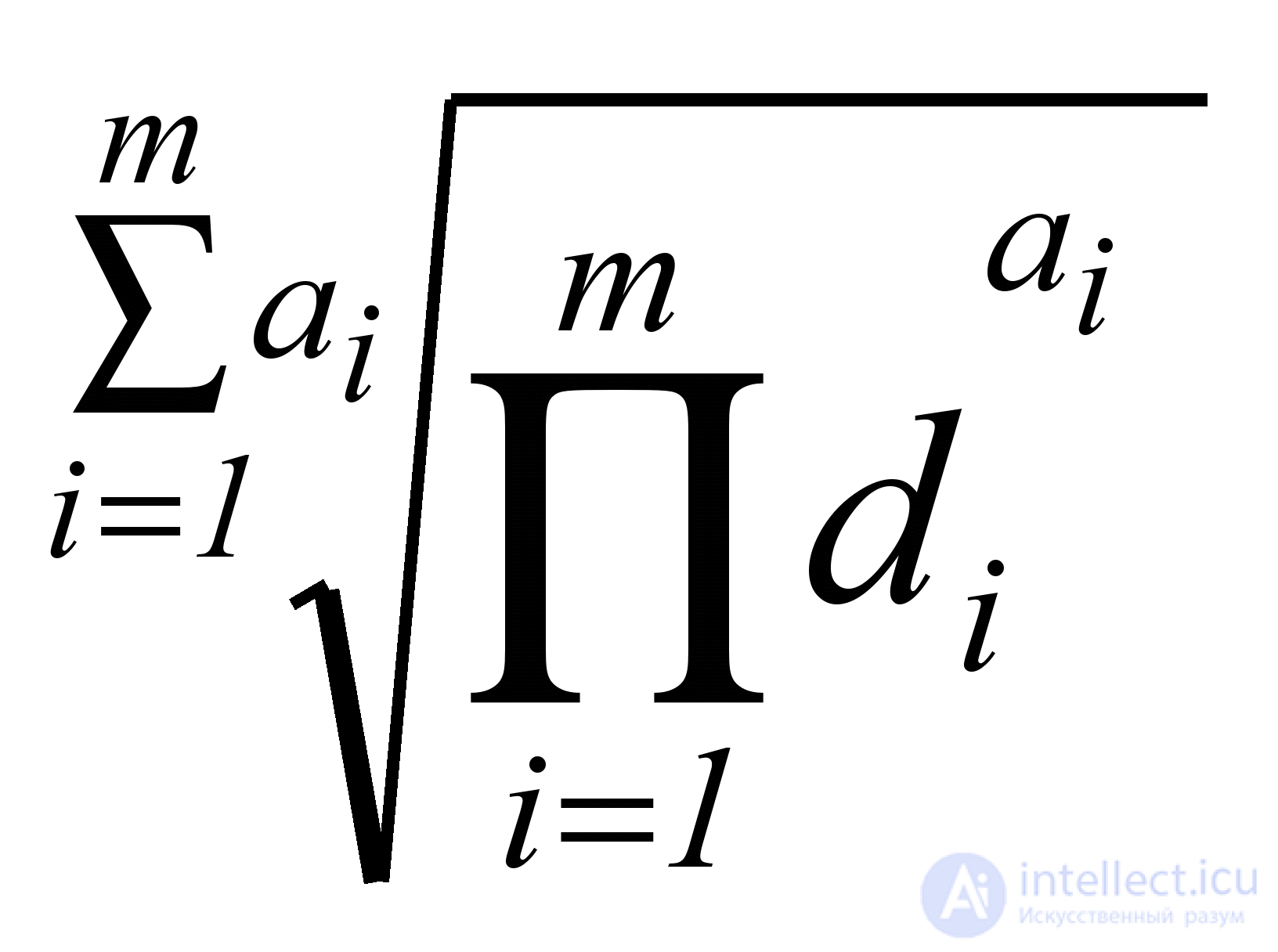, (5.3)

где di – частная функция желательности i-ой метрики, имеющей вес ai;

m – количество метрик в данной подхарактеристике.

Расчет производится в два этапа.

На первом этапе определяются единичные значения функции di (i = 1, 2, …, m) для любого количества откликов, каждый из которых должен представлять непрерывную монотонную функцию. Для случая возрастания качества с возрастанием числовых значений отклика предложены 3 типа зависимостей (типы 1, 2 и 3 на рис. 5.1), а для случая убывания качества с возрастанием числовых значений отклика предложены еще три типа зависимостей (типы 4, 5 и 6 на рис.5.2). При этом во всех случаях в качестве аргумента выступает отклик Y в своем натуральном виде – так, как он измерялся в ходе эксперимента, это большое достоинство для метода расчета.

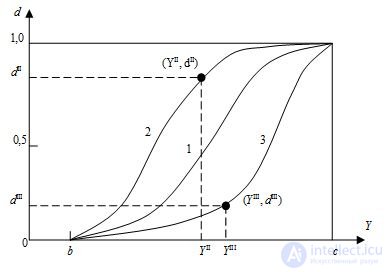
Рисунок 5.1. - Графики функций желательности трех возрастающих типов

 

Для всех трех типов возрастающих кривых определяющим является правильное назначение начала b и конца с физического (или допустимого) значения отклика Y, то есть должно соблюдаться условие

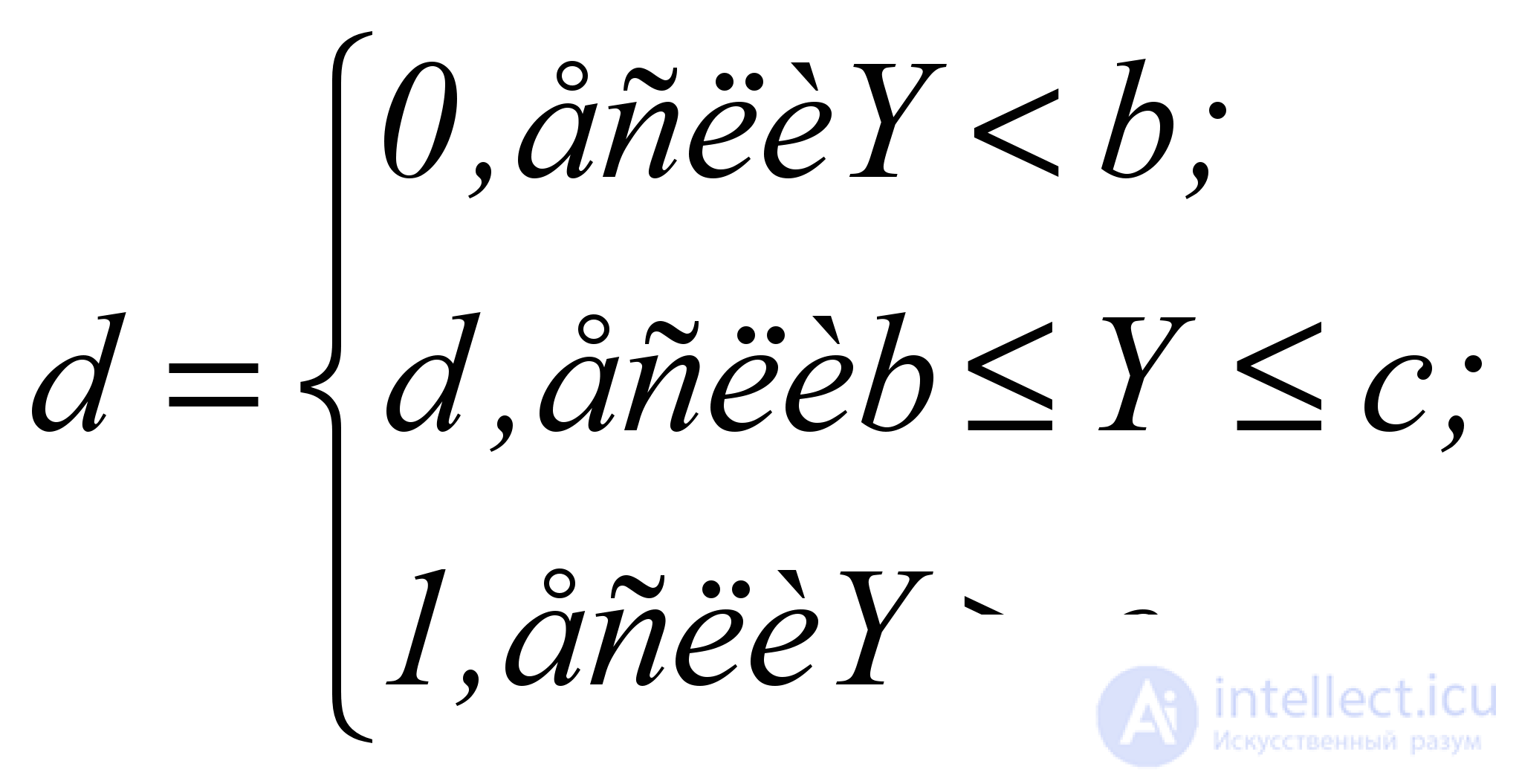 (5.4)

В этом случае кривая типа 1 является S-образной, возрастающей, симметричной и описывает качество отклика Y, если распределение Y не является резко асимметричным, по формуле

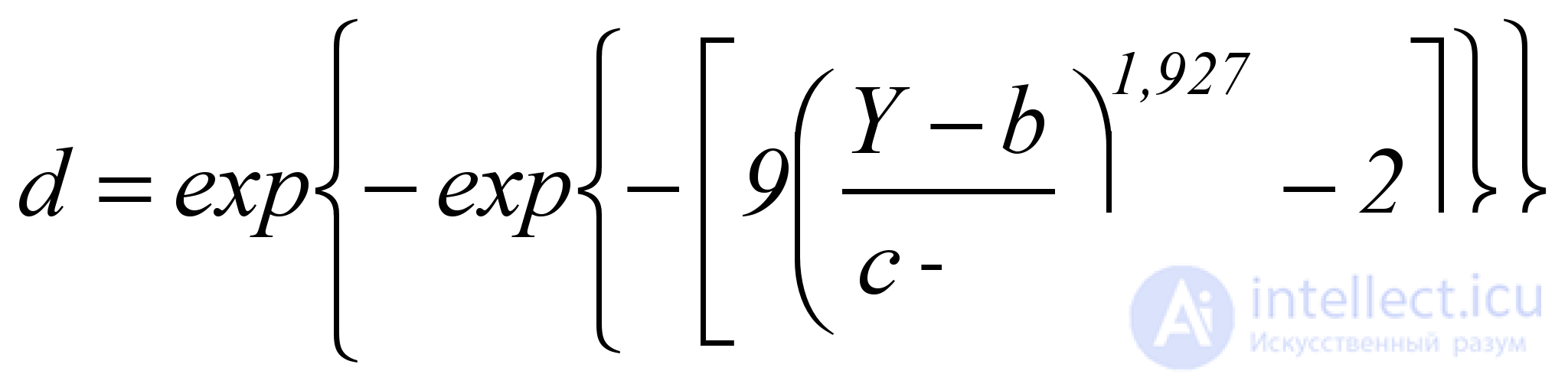. (5.5)

Кривая типа 2 является S-образной, возрастающей, асимметричной с быстрым начальным возрастанием и рассчитывается по формуле

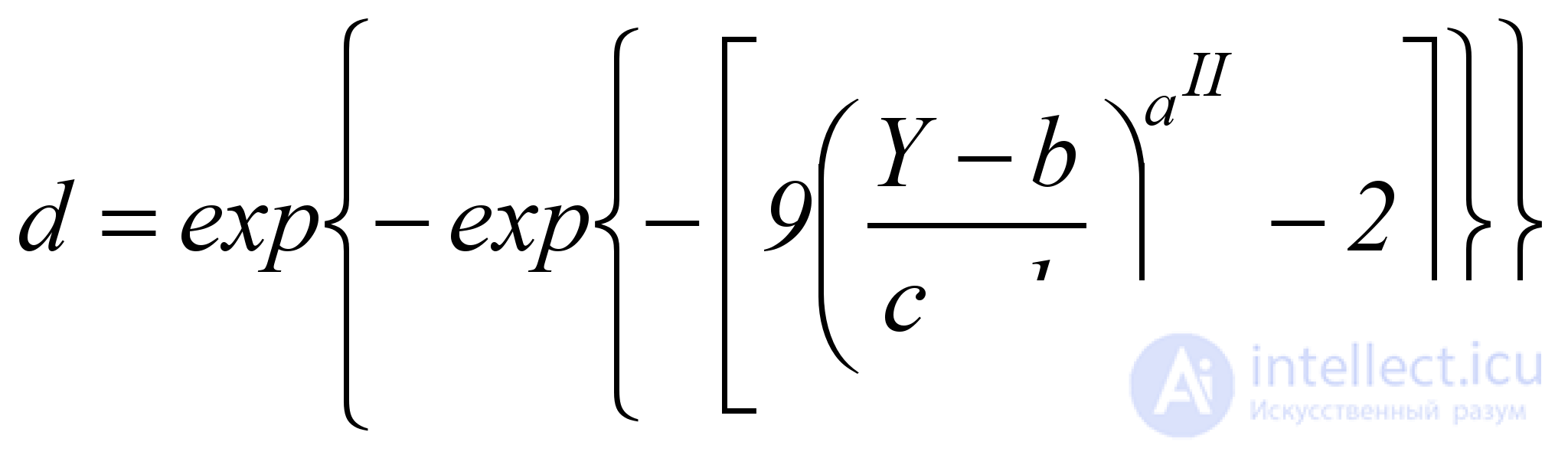, (5.6)

где показатель степени aII определяет скорость возрастания функции d. Для его расчета необходимо знать (или задаться) хотя бы одной точкой (YII; dII) на искомом графике. Тогда величину aII можно подсчитать по формуле

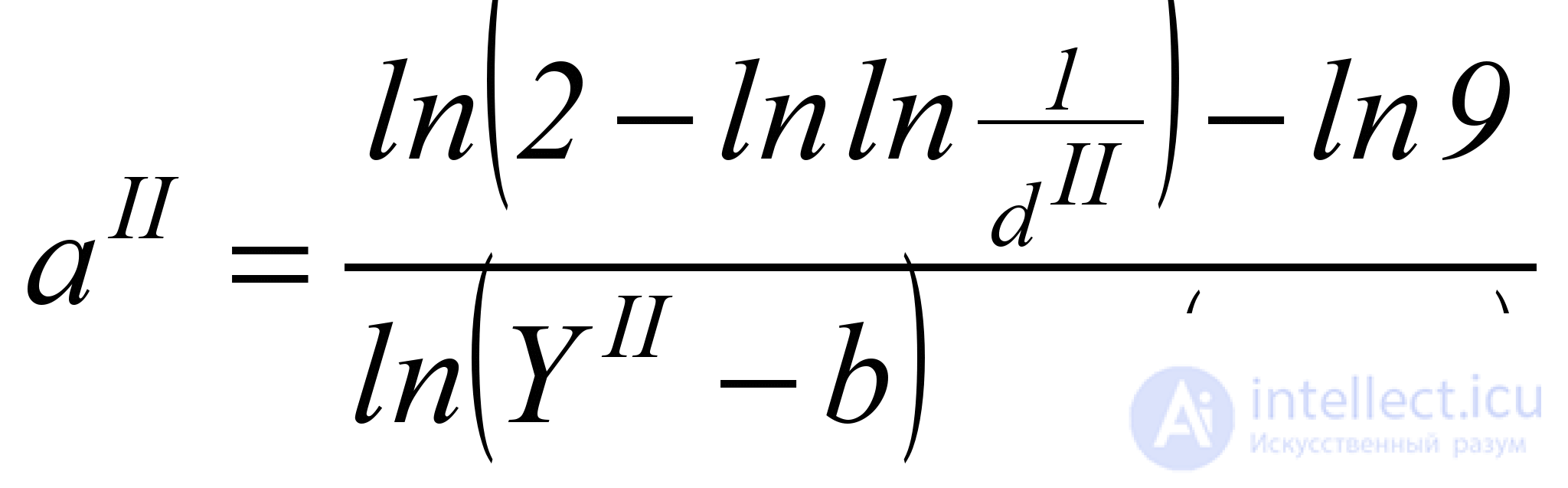 . (5.7)

Аналогично, кривая типа 3 является S-образной, возрастающей, асимметричной с медленным начальным возрастанием и рассчитывается по формуле

, (5.8)

где показатель степени aIII можно найти по единственной точке (YIII; dIII) по формуле

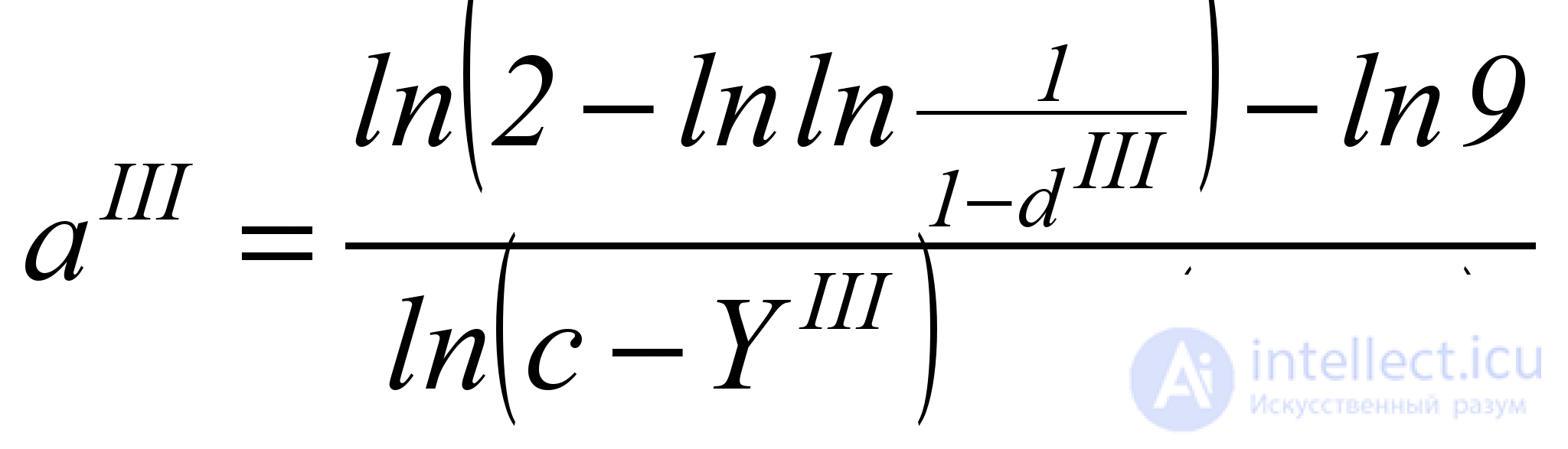 . (5.9.)

 

 

 

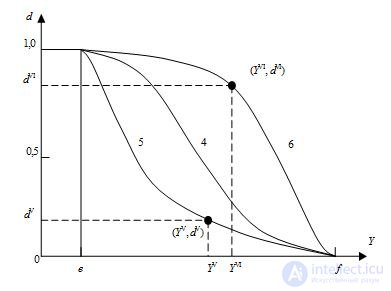
Рисунок 5.2 - Графики функций желательности трех убывающих типов

Для всех трех типов убывающих кривых определяющим является правильное назначение начала e и конца f физического (или допустимого) значения отклика Y, то есть должно соблюдаться условие

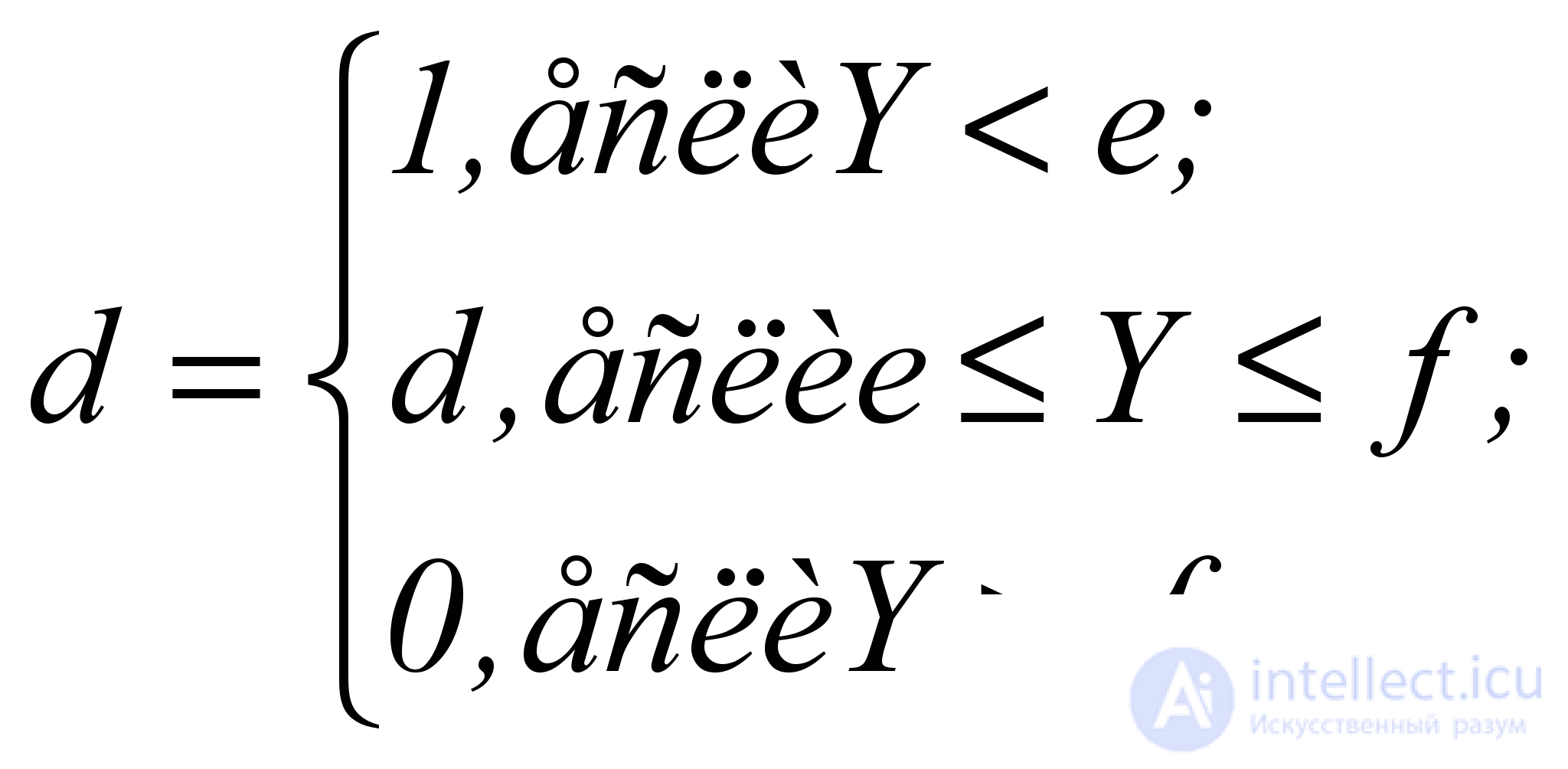 (5.10)

Кривая типа 4 является S-образной, убывающей, симметричной, представляет собой зеркальный вариант кривой типа 1, и описывается формулой

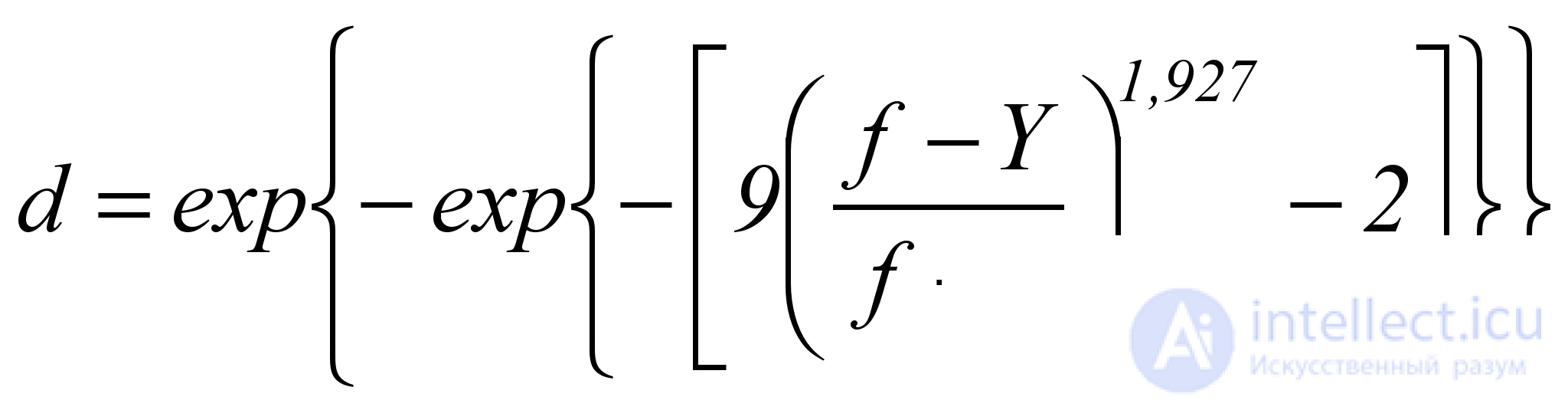. (5.11)

Кривая типа 5 является S-образной, убывающей, асимметричной, с быстрым начальным убыванием, представляет собой зеркальный вариант кривой типа 3, и описывается формулой

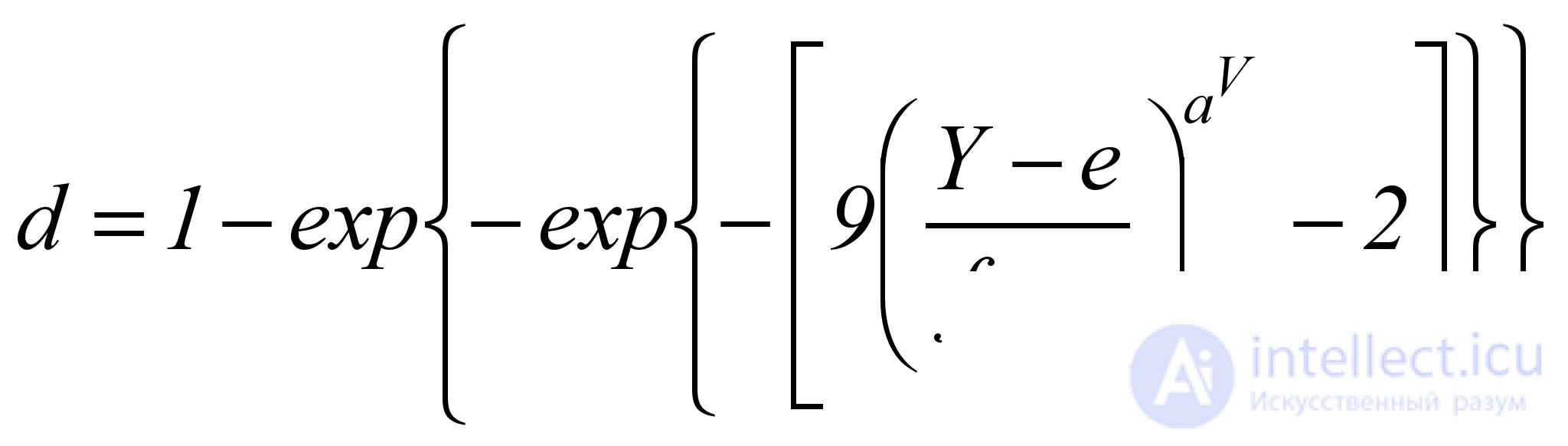, (5.12)

где показатель степени aV определяет скорость убывания функции d. Для его расчета необходимо знать (или задаться) хотя бы одной точкой (YV; dV) на искомом графике. Тогда величину aV можно подсчитать по формуле

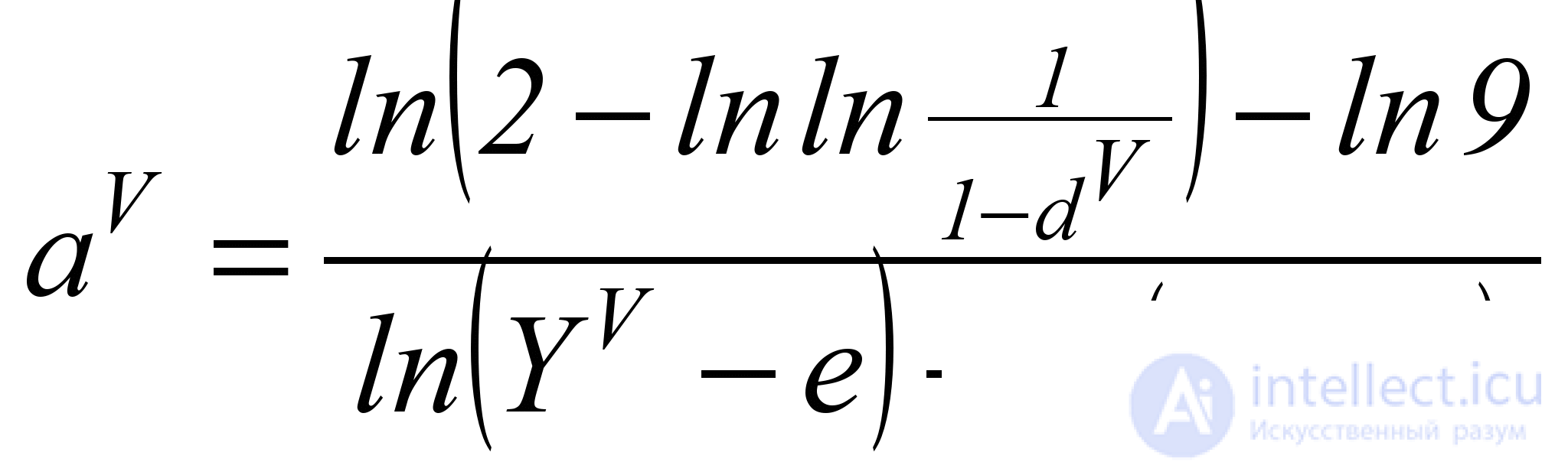 . (5.13)

 

Аналогично, кривая типа 6 является S-образной, убывающей, асимметричной, с медленным начальным убыванием, представляет собой зеркальный вариант кривой типа 2, и описывается формулой

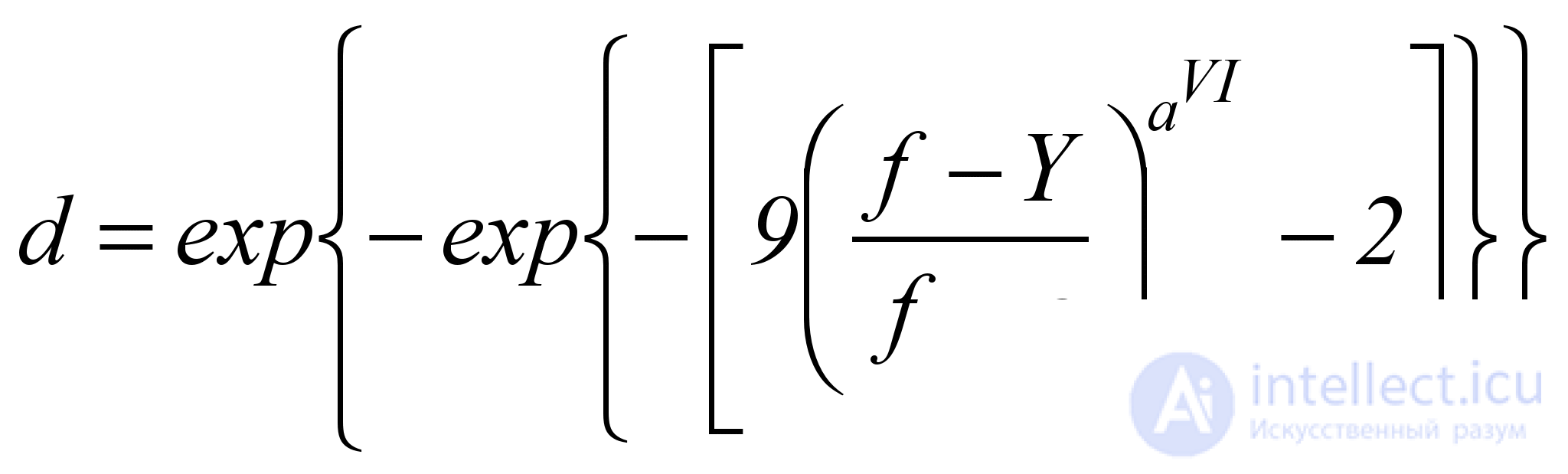, (5.14)

где показатель степени aVI можно найти по единственной точке (YVI; dVI) по формуле

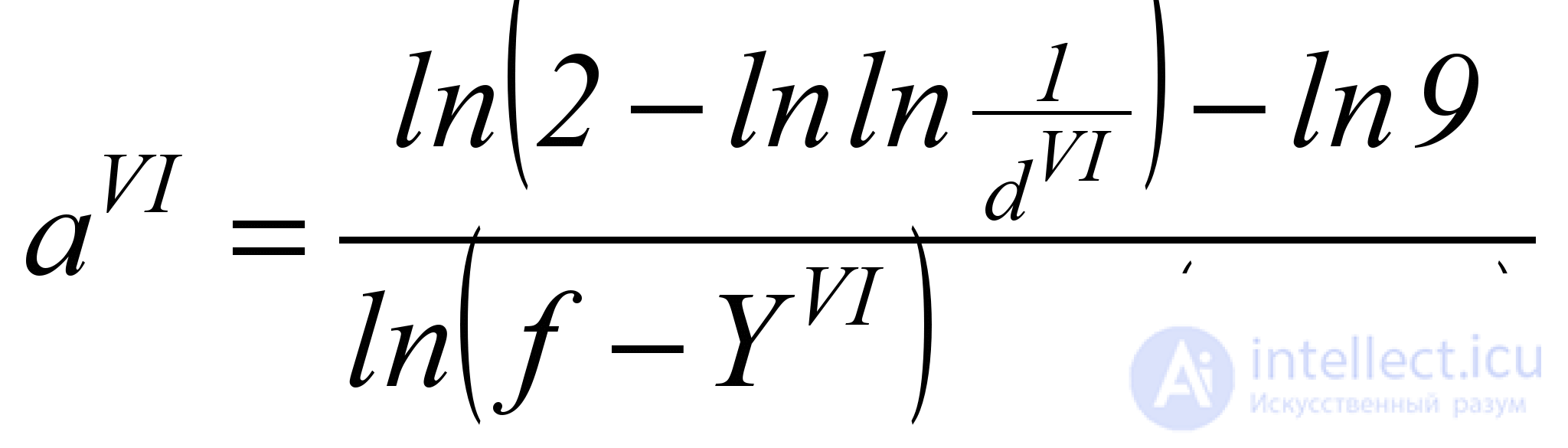. (5.15)

Если предположить, что количественные выборки имеют нормальный закон распределения (рис. 5.3), то получим следующие формулы для расчета частных показателей качества метрик di:

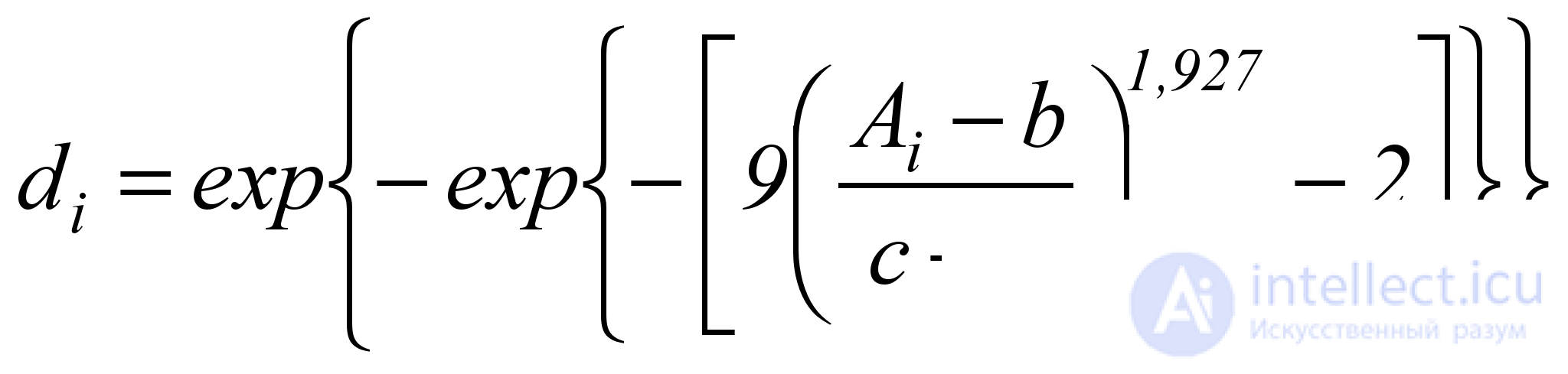, (5.16)

где di - показатель качества i-той метрики;

Ai – реальное значение i-той метрики;

b – минимально возможное значение i-той метрики;

c – максимально возможное значение i-той метрики.

 

Рисунок 5.3 – Нормальный закон распределения выборок

 

После расчета частных показателей качества метрик, рассчитывается обобщенная функция качества для каждой подхарактеристики (по формуле 5.3). Особенностью этого расчета является предварительное нахождение для каждого частного показателя di его веса ai. Для определения весов частных показателей качества ai используется метод весовых коэффициентов важности (ВКВ). Специалисты–программисты заполняют анкеты, в которых они оценивают значимость каждой метрики (пример анкеты на рис. 5.4).

 

 

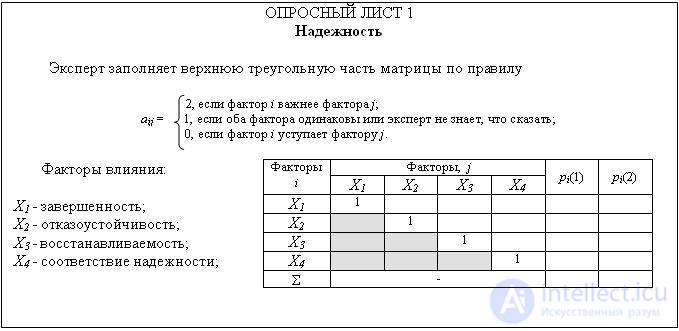
Рисунок 5.4 – пример анкеты для заполнения экспертами при использовании метода ВКВ

 

Ранжирование объектов сравнения с помощью экспертных методов обязательно включает процедуру проверки правильности полученных результатов. Для этого в методе весовых коэффициентов важности используются следующие 4 шага:

1. Рассчитывается коэффициент внутренней непротиворечивости ответов каждого эксперта. Если этот коэффициент меньше значения 0,5, то мнение данного эксперта отбрасывается;

2. Для оценки однородности мнений по каждому конкретному объекту применяется критерий Кохрена;

3. Рассчитывается коэффициент конкордации, который показывает степень однородности мнений экспертов;

4. Если разные группы экспертов дают противоречивые ответы на одни и те же вопросы, то применяется закон Ципфа

Затем по формуле 5.2 рассчитывается количественная оценка надежности программного продукта (предварительно для каждой подхарактеристики надежности должны быть определенны веса ak с использованием метода ВКВ)

 

 

Анализ данных, представленных в статье про количественная оценка надежности программного обеспечения, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое количественная оценка надежности программного обеспечения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Надёжность программного обеспечения

Из статьи мы узнали кратко, но содержательно про количественная оценка надежности программного обеспечения

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.