Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
Привет, Вы узнаете о том , что такое информационные процессы в дендритных структурах , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
информационные процессы в дендритных структурах , настоятельно рекомендую прочитать все из категории Нейробионика.
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
Информационные свойства нейрона существенно
зависят от процессов в его дендритах. Существуют
убедительные экспериментальные доказательства того, что
мембрана дендритов нейронов многих типов является
возбудимой (способна проводить активные потенциалы действия,
подобно тому, как это происходит в безмиэлиновых
аксонах). Теоретическое рассмотрение информационных
свойств нейронов с активными дендритами, основанное на
данных физиологии, морфологии и результатах
моделирования распространения возбуждения в нервных
волокнах, позволяет считать, что в дендритной системе
происходит наиболее значительная переработка информации,
поступающей к нейрону. Рассмотрение морфологических
зарисовок нейронов с развитыми дендритами с учетом
возможных информационных процессов в дендритах
позволяет по-новому взглянуть на нейрон, а также и на
целую сеть из таких нейронов: модель нейрона
представляется теперь в качестве многовходового и многовыходо-
вого элемента. При этом подразумевается, что нейрон
имеет несколько функционально различных выходов.
Кроме традиционного аксонного выхода,
разветвляющегося на ряд коллатералеи, нейрон дополнительно может
иметь несколько «дендритных выходов», т. е. обладать
способностью передавать возбуждение непосредственно
с некоторых участков дендритного дерева на дендриты,
сому или аксон соседних нейронов. Появление импульса
на аксонном выходе рассматриваемого нейрона
необязательно.
Информационные преобразования могут происходить
во взаимосвязанных дендритных структурах нейронной
сети, приводя к появлению импульсов на аксонных
выходах каких-либо нейронов сети лишь при реализации
в дендритной структуре многих нейронов определенных
операций.
Перечисленные сведения позволяют сформулировать
концепцию о том, что переработка информации в сетях
из нейронов с развитыми дендритами в значительной мере
определяется информационными процессами в
дендритных структурах.
Концепция основана на трех положениях,
установленных в результате экспериментальных исследований мор-
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
фо логов и физиологов и работ по моделированию дендри-
тов: 1) нейроны имеют дендро-дендритные контакты;
2) существуют механизмы эффективной передачи
возбуждения от дендрита к дендриту; 3) основная переработка
информации, поступающей к нейрону, осуществляется
в его дендритах. Основные результаты, подкрепляющие
эти положения, следующие.
1. Морфологически показано, что, кроме аксо-аксо-
нальных синапсов, нейроны могут иметь
дендро-дендритные синапсы, а также участки непосредственного
контактирования отростков друг с другом без
структурного изменения их мембран. Такие формы взаимодействия
возможны как между дендритами одного нейрона, так и
между дендритами разных нервных клеток. Некоторые
специализированные длинноаксонные нейроны
первичных слуховых центров имеют тип ветвления дендритов,
обеспечивающий многократное соприкосновение отростков
друг с другом, пространственное перекрытие и соединение
отдельных ветвей плазматическими перемычками
(анастомозами). Во многих отделах мозга существуют зоны
концентрации дендритов разных нейронов. В новой коре
больших полушарий апикальные дендриты пирамидных
клеток III и V слоев образуют своеобразные пучки,
которые рассматриваются как компонент столбчатой
организации коры [6], но могут быть и морфологическим
субстратом для прямого взаимодействия дендритов.
Характер организации такого пучка не случаен —
составляющие его дендриты расположены очень компактно, зачастую
на расстояниях от 20 нм до 1—3 мкм, причем между
дендритами отсутствуют глиальные отростки [5].
2. По физиологическим данным [102]
дендро-дендритные влияния могут осуществляться посредством прямого
химического или электрического воздействия
возбужденных участков мембраны дендрита на мембрану близко
расположенных дендритов соседних нейронов. Наличие
у дендритов некоторых типов нервных клеток мозга
позвоночных способности к активному проведению
потенциалов действия облегчает передачу возбуждения от
одного дендрита к другому. Прд этом повышается
эффективность влияния через медиаторные дендро-дендритные
синапсы, через не имеющие структурного изменения участки
контактирования мембран дендритов. Усиливается
электрическое и химическое влияния на мембрану близко
расположенных дендритов, так как электрохимические транс-
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
мембранные токи в активных дендритах существенно
больше, чем в пассивных, способных проводить лишь
медленные потенциалы. Активными являются дендриты
пирамидных клеток гиппокампа, неокортекса, клеток
Пуркинье мозжечка, некоторых мотонейронов [102].
3. Моделирование на ЭВМ информационных
процессов в элементарных звеньях дендритов: локальных
утолщениях — варикозностях, фрагментарностях, узлах
ветвления, шипиках, располагающихся на активных
дендритах, показало, что в них возможно выполнение ряда
логических и арифметических операций. Характер
выполнения операций существенно зависит от управляющих
воздействий, подаваемых в звенья [46], которыми в
естественных условиях могут служить непосредственные
электрохимические или синаптические дендро-дендритные
влияния.
2.2.1. Общее представление
о возбудимых процессах в дендритах
В случае невозбудимой (пассивной) мембраны дендритов
передача синаптического воздействия происходит только
«электротонически», т. е. после срабатывания синапса
в прилегающем участке дендрита возникает ВПСП
(возбуждающий постсинаптический потенциал), который
распространяется с затуханием по дендриту к соме [96].
Изменение потенциала сомы в этом случае определяют
следующие два фактора: 1) мощность возбуждения
(фактор, определяющий величину поляризующего тока,
протекающего через субсинаптическую мембрану, зависящий
от размеров возбуждающего синапса); 2) длина и диаметр
дендрита, связывающего данный синапс с сомой (факторы,
определяющие затухание и изменение формы ВПСП).
Чем больше мощность возбуждения (размеры
возбуждающего синапса) и меньше расстояние от данного
синапса до сомы, тем больший вклад в ВПСП сомы даст
данный синапс.
В случае активной или возбудимой мембраны
возникновение активного процесса (импульса) возможно в
любой точке мембраны дендритов. Возникнув, импульс
распространяется как в сторону сомы, так и в
противоположном направлении. Чем тоньше дендрит, тем больше в нем
изменение ВПСП при срабатывании одинаковых
синапсов. Поэтому при возбудимой мембране генерация импуль-
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
са в дендрите возможна в ответ на гораздо меньшее число
пресинаптических импульсов, вследствие чего диетальные
синапсы можно в ряде случаев считать более
приспособленными для передачи импульсов «один к одному», чем
соматические.
После того, как в дендрите возник активный импульс,
он без затухания распространяется до места изменения
свойств мембраны или конфигурации волокна, например
резкого расширения, в частности, точки ветвления ден-
дритов. Импульс может преодолеть точку ветвления и
продолжить распространение к соме или, напротив,
блокироваться в зависимости от состояния других веточек,
сходящихся в этой точке. Если другие веточки находятся
в возбужденном состоянии или деполяризованы, то их
шунтирующее действие уменьшено, что создает
благоприятные условия для прохождения импульса. В противном
случае импульс гаснет (мембрана не возбуждается),
переходя в импульс типа ВПСП, который электротони-
чески (с затуханием) распространяется к соме, внося свой
вклад в повышение ее потенциала. Чем дальше к соме
продвинулся такой импульс, тем больше этот вклад. На
основании изложенного можно ввести еще два фактора,
определяющих зависимость изменения внутреннего
потенциала сомы от приходящих воздействий: 3) архитектоника
дендритных ветвлений; 4) расположение синапсов на этих
ветвлениях. Речь идет о соотношениях между отрезками
дендритов, связывающих между собой синапсы, а также
синапсы с местами геометрической неоднородности
(расширения, узлы ветвления).
Резюмируя вышесказанное, делаем заключение, что
дендритная система произвольной конфигурации может
быть представлена в виде набора из простых дендритных
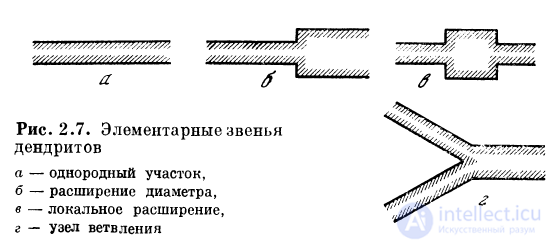
образований — элементарных звеньев (рис. 2.7).
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
Моделирование на ЭВМ и теоретическое исследование
процессов возбуждения в таких звеньях [43, 46] показало,
что в них может выполняться ряд логических и
арифметических операций.
2.2.2. Резкое расширение. Трансформация ритмов
При моделировании на ЭВМ получено следующее. По
длинному однородному волокну импульс движется с
постоянной скоростью, которая зависит от диаметра d и
свойств мембраны, характеризующих ее возбудимость.
По мере приближения к расширению наблюдается
убывание скорости и амплитуды как одиночного импульса
[8], так и импульсов в серии [9, 35]. Эти изменения
объясняются тем, что вследствие обратной пропорциональности
между входным сопротивлением волокна и его диаметром
большая доля тока из зоны генерации начинает отдаваться
в расширенную зону. Таким образом, расширение
оказывает шунтирующее действие на приближающееся
возбуждение. Шунтирующее влияние расширения может
настолько уменьшить скорость и амплитуду импульса,
что процесс активного возбуждения мембраны
прекратится. Коэффициент расширения волокна К0 (отношение
диаметров широкой и узкой частей), при котором
происходит блокировка импульса, будем называть
критическим расширением. Для волокна с параметрами аксона
кальмара критическое расширение К0 = 5,5. Однако
в общем случае свойства мембраны разных волокон могут
различаться, и значения К0 будут различны для разных
состояний мембраны.
Итак, при К ^> К0 импульс блокируется и не
проходит в расширенную часть; при К < К0 импульс
преодолевает расширение и продолжает свое движение по
расширенному волокну.
Трансформация ритмов. При высокой частоте
следования импульсов по волокну его мембрана не успевает
восстанавливать свои возбудимые свойства после
прохождения каждого из них. Поэтому проведение каждого
последующего импульса ухудшается, монотонно убывает
амплитуда и скорость импульсов. В итоге в некоторой точке
волокна очередной импульс может погаснуть. В
однородном волокне такой точкой является точка стимуляции.
В волокне с расширением (К <[ К0) выпадение импульсов
происходит в месте изменения диаметров, чему способст-
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
вует шунтирующее действие расширенной части волокна.
Если на части волокна возбудимость мембраны снижена
(введена функциональная неоднородность), то
выпадение импульсов происходит в точке, где меняется
возбудимость [9]. Чем ближе К и К01 тем чаще выпадают
импульсы.
После блокировки импульса расширенная часть
волокна успевает восстановить свою возбудимость, так как
интервал между двумя соседними импульсами удвоился
и последующие импульсы снова смогут пройти
расширение. В итоге импульсная последовательность оказывается
трансформированной. Трансформация зависит от частоты
следования импульсов, коэффициента расширения и
свойств мембраны [35].
В общем случае возможны трансформации
последовательностей типа (N + К, К), что означает, что из каждой
пачки в N + К импульсов на конце волокна
обнаруживается только N импульсов, К импульсов блокируется.
Приближенно можно считать, что подобная
трансформация объясняется тем, что за каждым распространяющимся
импульсом остается следовой потенциал
гиперполяризации. В результате суммирования следовых потенциалов
понижается уровень мембранного потенциала волокна,
а это эквивалентно увеличению порога раздражения
волокна и приводит к выпадению некоторого импульса.
В месте расширения условия для выпадения импульса
наиболее благоприятны, так как здесь входное
сопротивление мембраны волокна меньше. При определенной
частоте суммирование следовых эффектов может настолько
снизить амплитуду импульса, что ВПСП в расширении
станет меньше порогового и произойдет его блокировка.
Итак, пусть к расширению нервного волокна
(дендрита) поступают импульсы с частотой v. При этом v
меньше 1/т#, где %п — минимальный период следования
импульсов для данного волокна (абсолютная рефрактер-
ность). Через некоторое время в волокне установится
стационарный процесс типа периодики (N + К, К). При
К = 1, т. е. когда после блокировки одного импульса
устанавливается некоторый динамический уровень
равновесного мембранного потенциала, с которого
начинаются циклы периодики (п + 1, 1), для N получим
соотношение (случай, когда
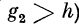
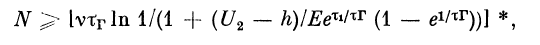
где v — частота следования импульсов по волокну; g2 —
амплитуда потенциала в волокне диаметром d2; тг —
достоянная восстановления нормального значения g0 от
уровня гиперполяризации; Е — максимальная
амплитуда гиперполяризации; h — порог возбуждения волокна;
х1 — время от момента возникновения импульса до того
момента, в который следовой потенциал экстремален,
внешние квадратные скобки означают, что от выражения
в них берется целая часть.
Если h^> g2, то блокируется К первых импульсов.
Соотношение для К:
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
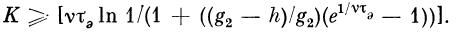
Посредством изменения мембранного потенциала g0M
(а следовательно, и порога h = g0 — g0M) можно
получить трансформации типа (N + К, К). При т
расширениях (узлов ветвления и т. п.) средняя частота нервных
импульсов vm на выходе т-то расширения (узла)
определяется из рекуррентного соотношения:
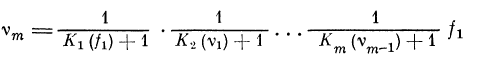
(для случая h > g2i). Здесь vt — средние значения частот
следования импульсов после прохождения i-то
расширения (узла), £—1, 2, 3, . . ., т.
В зависимости от числа ответвлений, расположенных
на пути от входа до сомы, каждый дендритный вход
нейрона характеризуется своей чувствительностью. Нейрон
отвечает на приходящий сигнал, если частота следования
импульсов v больше некоторого критического значения. Об этом говорит сайт https://intellect.icu .
Например, если встречается один узел (расширение),
то Vj. должна быть больше v*, где
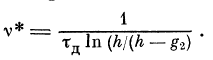
При изменении поляризации узлов пороговые
чувствительности могут меняться. Таким образом, дендрит
с утолщением (в частном случае — узлом ветвления)
может служить делителем частоты следования импульсов
с управляемым коэффициентом деления (управление
может осуществляться синапсами, расположенными на
утолщении), а также фильтром верхних частот.
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
2.2.3. Локальное расширение
Локальными расширениями называются расширенные
участки волокна длиной менее трех констант длины.
Протяженность локальных расширений значительно меньше
зоны, которую занимает распространяющийся по
волокну нервный импульс (в 4—10 раз). Как и в случае
«нелокального» расширения, по мере приближения импульса
к области локального расширения его амплитуда и
скорость убывают. Показано, что в локальном расширении
импульс существенно задерживается. Величина задержки
зависит от протяженности расширенной части и
коэффициента расширения К. Критическое расширение К0 (при
котором импульс блокируется) увеличивается при
уменьшении длины расширенного участка. При длинах
расширенной части волокна I порядка X импульс может
преодолеть большие расширения, чем в случае, когда
протяженность расширенного участка I ^> X.
2.2.4. Узел ветвления
Импульсы, идущие по сходящимся волокнам,
взаимодействуют в узле. Результат взаимодействия — появится
на выходе узла импульс или нет — определяется
соотношением диаметров волокон, различием в моментах
прихода импульсов к узлу, а также возбудимыми свойствами
мембраны узла.
Основным характеристическим параметром узла с
одинаковыми входными волокнами является коэффициент
расширения К = d2ldx — отношение диаметров выходного
и рассматриваемого входного волокон. Если К < К0, то
через узел пройдет даже одиночный импульс; если К
очень велико, то импульсы вообще не могут преодолеть
узел. В некотором диапазоне значений К импульс на
выходе появляется только в том случае, когда к узлу
подойдут два входных импульса — каждый по одному из
входных волокон, при этом допускается некоторое
различие At в моментах их прихода. Интервал At может
изменяться, это скажется на амплитуде, задержке и на
самом факте появления выходного импульса (в реальных
условиях — на вероятности прохода импульсов через
узел).
При одновременном приходе в узел ветвления двух
спайков напряжение в узле g7 = g21 + g22 = 2g2. В слу-
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
чае когда gy больше h, возбуждение преодолевает узел.
По-видимому, условия для прохождения импульса через
узел выполняются, если h/2^ g2 <fe, что возможно
при определенном К = d2ldx. Пусть время прихода
второго импульса t2 = t1 + Д£, тогда условие прохода
импульса через узел будет gy = g2 (1 + е~Л'/Тд) >• h, отсюда
At <^ Д^тах = ^д In {gj{h — £2))- Из последнего
соотношения видно, что выполнение функций непрерывной
логики «идеальное совпадение» (проход импульсов через
узел) будет выполняться тем точнее, чем меньше тд
(определяется свойствами мебраны) и чем больше h превышает g2.
Операции над последовательностями. При поступлении
к такому узлу по ответвлениям пачек импульсов с
достаточно большими интервалами между ними (Д^, i+i^> Д^тах)
на выходе узла будет пачка импульсов, расставленных
соответственно моментам совпадения импульсов.
Представим пачки импульсов в виде векторов | = (£15 £2,...
. . ., 1п) и г] = (т1ь . . ., т)п), где ^ и y\t принимают
значения нуль или единица, соответствующие отсутствию или
наличию в данный элементарный интервал времени
импульса на соответствующем входе узла. Размерность
векторов определяется длительностью большей пачки. Для
меньшей пачки интервалам, остающимся после ее
окончания соответствуют нули в векторной записи
последовательности. Средняя частота следования импульсов по
дендриту на выходе узла: vBbiX = (£, i\)/TmH, где (§, т]) —
скалярное произведение векторов, а Тиан — длительность
меньшей пачки.
При наличии в узле ветвления производящих
дополнительную деполяризацию (или гиперполяризацию)
«управляющих синапсов» возможно выполнение операций
«скалярного произведения» частот следования импульсов
по одному из ответвлений и частот повторения
подаваемых на управляющий синапс деполяризационных
сдвигов увых = т (vBX/s) при возбуждающем управляющем
синапсе в узле ветвления, или операции vBUX = vBX —
—t (vbx/s) при тормозном синапсе. Считаем, что
управляющие синапсы создают сдвиги деполяризации Ags, такие,
что Ags + g2 ^ h, продолжительностью т, с частотой
повторения /s. В случае управляющих возбуждающих
воздействий расширение узла больше критического, в
случае тормозных — меньше критического. Таким образом,
в узле ветвления дендрита могут выполняться операции,
аналогичные тем, которые выполняет аналоговый
нейрон [46]. Узел ветвления с неодинаковыми входными волокнами.
В зависимости от соотношения диаметров,
составляющих узел волокон, возможно выполнение разных
операций: «И», «ИЛИ», «НЕ». Например, рассмотрим узел,
диаметр первого входного волокна которого в полтора
раза меньше диаметра второго и в пять раз меньше
диаметра выходного волокна. Исследованная на ЭВМ модель
такого узла описана в работе [26]. Если возбуждается
только первое волокно, импульс в таком узле блокируется,
если возбуждается только второе волокно, то импульс
проходит через узел ветвления. Предварительное
возбуждение первого волокна может блокировать импульс,
приходящий по второму волокну, это произойдет в том
случае, когда второй импульс попадет в фазу рефрактер-
ности, созданную первым. Таким образом, первое волокно
оказывается запрещающим для сигнала, идущего по
второму волокну. Расчеты показали, что этот эффект
наблюдается при условии, что первый импульс опережает
второй на At = 1,7—2,8 мс.
Узел ветвления с локальным расширением. В таком
узле волокна, перед тем как слиться, несколько
расширяются, претерпевая скачкообразное расширение
протяженностью I меньше X. Это приводит к тому, что в таком
узле надежность проведения возбуждения становится
выше, чем в аналогичном узле без расширения. При
К^>К0 импульсы проходят через узел при больших
Дт [26].
2.2.5. Управление операциями
в дендритных структурах
Существующие в нервной системе способы воздействия
на активную мембрану дендритов и аксонов служат как
для создания активных нервных импульсов в разных
участках нервной клетки, так и для управления процессом
их прохождения по дендритам к соме клетки.
Следовательно, направленное изменение свойств мембраны, как
местное с помощью поступающих от синапсов сигналов,
так и на большей области посредством гуморальных
воздействий, способно управлять характером
распространения возбуждения, осуществляя тем самым переработку
информации.
Из работ по математическому моделированию на ЭВМ
распространения возбуждения при различных изменениях
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
свойств мембраны волокна (имитирующих синаптические
управляющие воздействия) следует, что изменение свойств
мембраны позволяет:
управлять скоростью распространения возбуждения
по волокну типа аксона или дендрита; в частности,
эффективным способом управления задержкой в проведении
активного импульса являетсй изменение состояния
(деполяризации) локального расширения волокна;
управлять величиной критического расширения
дендрита (аксона), при котором наступают блокировки
импульса, и тем самым либо пропускать, либо блокировать
одиночные импульсы, либо изменять вид периодической
импульсной последовательности или произвольной
комбинации импульсов;
управлять величиной критического временного
интервала At, в пределах которого приход двух импульсов
к узлу обеспечивает появление выходного импульса,
и переводить узел из состояния, когда пропускается
одиночный импульс, в состояние, когда выходной сигнал
появится только в результате совпадения двух входных
импульсов, т. е. из режима «ИЛИ» в режим «И».
Из перечисленных выводов об операциях, которые
реализуются за счет управляющих воздействий, подаваемых
в элементарные звенья дендритных структур, следует, что
наиболее легко осуществимым способом кодирования
информации в дендритных структурах нервной системы
является кодирование временем появления импульса и
величинами временных интервалов между импульсами.
2.3. Информационные процессы
в локальных цепях дендритных структур
В разделе рассматриваются операции, которые могут
быть реализованы в нейроподобных сетях,
организованных по типу локальных цепей, т. е. структур, в которых
существуют дендро-дендритные взаимодействия.
Рассматриваются случаи пассивной и активной дендритной
мембран. Приводятся примеры реализации таких
операций, как выделение максимального из нескольких входных
сигналов, модуля разности сигналов, определенной
частоты следования импульсов и др.
2.3.1. Пассивные дендриты
Пусть на однородный пассивный участок дендрита,
константа длины которого X, к расположенным на этом
участке синапсам с11 с2, . . ., сп приходят спайки с частотами
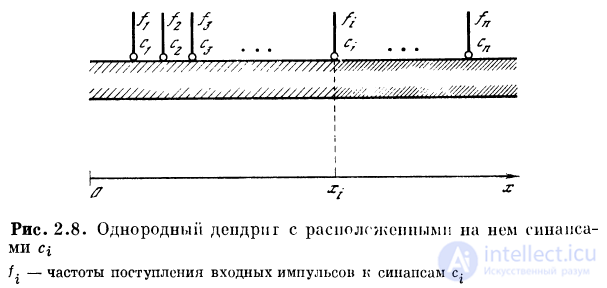
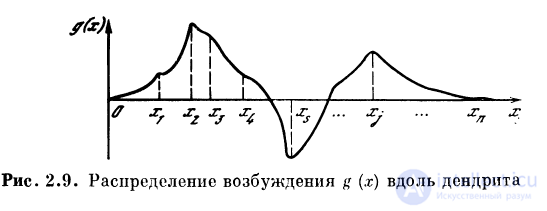
следованияД, /2, . . ., /п (рис. 2.8). Распределение
потенциала g (х) вдоль дендрита будет иметь вид (рис. 2.9)!
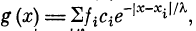 , где i = 1, 2, . . ., гг. Обозначим
, где i = 1, 2, . . ., гг. Обозначим
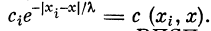 . Коэффициент
. Коэффициент 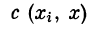
характеризует вклад ВПСП от синапса с{ в точке х{ в величину
ВПСПв точке х. Назовем 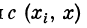 функцией связи точки xt
функцией связи точки xt
с произвольной точкой х волокна.
Ограничиваясь рассмотрением дискретного набора
участков дендрита, расположенных вблизи синапсов
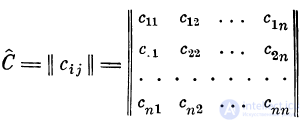
съ с2, . . ., сп, введем коэффициенты связей 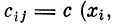
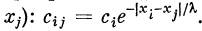 . Коэффициенты связей Сц представим
. Коэффициенты связей Сц представим
в виде матрицы
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
Введем вектор входного возбуждения f и вектор выходного
возбуждения g:
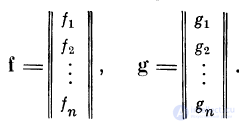
Связь между g и f можно записать в матричной форме
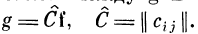
Величина компонента вектора выходного возбуждения
Так как рассматриваемое волокно (дендрит) может
иметь дендро-дендритные контакты с другими волокнами
такого же типа, то результирующее значение ВПСП
в волокне будет определяться суммой воздействий:
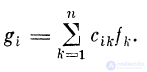
вектором входного возбуждения, помноженным на матрицу
связей, и вектором выходного для других дендритов воз-
буждения, помноженного на матрицу связей между этими
дендритами. Вектор возбуждения первого дендрита
назовем первичным и будем обозначать g1. Вектор возбуждения
второго дендрита назовем вторичным и будем
обозначать g2. Связь между g1 и g2 может быть записана
следующим образом:
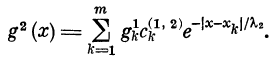
Здесь g2 (х) — ВПСП во вторичном волокне, g\ — ВПСП
вблизи к-то дендро-дендритного синапса, связывающего
первичный дендрит со вторичным, Х2 — константа длины
boJ втором волокне.
Введем вектор g2 и его компоненты g\:
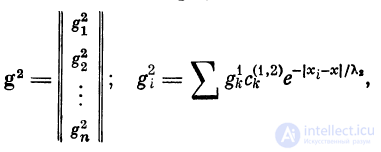
где cki = c(i}'2)e '%i ^ 2. Связь между векторами g1 и g2
будет g2 = || c[\'2) || g1, где || с*1*2) || — матрица связей первого
волокна со вторым; g2 можно выразить через f: g2 =
= || 4V2) || g1 = || с{\2) || • || c{j || f. При многократной передаче
возбуждения с одного дендрита на другой для вектора
возбуждения g' (ВПСП на дендрите номер I) получим
соотношение
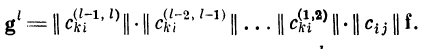
То есть вектор возбуждения g^paBeH результату
воздействия произведения матриц связей всех предыдущих
дендритов на вектор входного возбуждения:
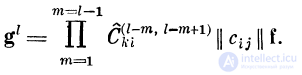
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
Для дендритных структур, в которых возбуждение
тг-кратно передается с первого дендрита на второй, а со
второго на первый, получим g^ = (Ё — (С1С2)п)(Ё -—
— C1C2)~~iCi, где g\ — вектор возбуждения в первом
дендрите на п-м такте передачи возбуждения. В
установившемся режиме
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
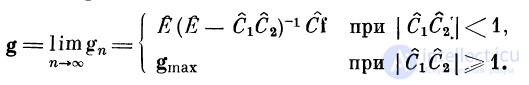
Проведенное рассмотрение показывает, что
однородный участок пассивного и активного дендритов (при
условии, что мембранный потенциал ниже уровня порога
активного возбуждения) может служить функциональным
элементом с широкими функциональными возможностями.
Дендритная сеть из таких элементов может выполнять
различные информационные преобразования, характер
которых определяется структурой связей — матрицей
II сн \\.
Входные и выходные векторы различных дендритов
сети могут рассматриваться в качестве описывающих
сенсорные образы внешней или внутренней среды
случайных векторов. Результаты матричных преобразований
над векторами поэтому могут, в частности, представляться
в виде статистических характеристик, аналогичных тем,
которые используются в статистической теории
распознавания образов [39]. Например, если коэффициенты с$
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
(веса синапсов) пропорциональны вероятностям прихода
сигналов, то выходной вектор g при конкретном входном
векторе f будет тем больше по модулю, чем меньше
различие между g и вектором математического ожидания
сигналов. Максимум модуля g будет тогда, когда входной
вектор равен вектору математического ожидания
сигналов. Таким образом, разные дендриты некой сети могут
представляться в качестве детекторов определенного
входного вектора — детекторов определенного «образа»,
характеризующего внешний мир или внутреннее
состояние искусственной или естественной информационной
системы (в частности, живой системы). Если
придерживаться концепции П. К. Анохина о том, что внутриден-
дритные трубочки способны передавать к соме
информацию о величине возбуждения вблизи синапсов,
располагающихся вдоль дендрита, то можно предполагать, что
в соме может возникнуть возбуждение, пропорциональное
сумме компонентов выходного вектора возбуждения
дендрита, т. е. пропорционально модулю g. Если допустить,
что при посредстве таких трубочек возможна передача
сигнала, пропорционального величине возбуждения
одного синапса, к другому синапсу и при этом с разными
коэффициентами, то эффективная матрица коэффициентов
связей локальных участков дендрита может существенно
отличаться от диагональной. То есть матрица || с^ \\ может
быть произвольной. Такое допущение позволяет
предполагать, еще более широкие функциональные возможности
дендритов, так как теперь матричные преобразования
могут быть произвольными.
2.3.2. Активные дендриты.
Управление проведением возбуждения
Рассмотрим однородный участок волокна (дендрита), на
синапсы с1? с2, с3, . . ., сп которого приходят импульсы
с частотами /х, /2, /3, . . ., fn соответственно. Константа
длины волокна — Я, порог возбуждения — h. В тех
случаях, когда ВПСП в волокне не превышает порог
возбуждения h, характер распределения ВПСП (функция
g (x)) вдоль волокна будет иметь вид, как в случае
пассивного волокна:
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
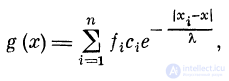
где i = 1, 2, 3, . . ., п. Связь между векторами f и g
будет g - || си || f.
При проведении активным волокном, вдоль которого
неравномерно распределен ВПСП, импульса характер
движения импульса будет зависеть от характера
распределения ВПСП вдоль волокна. Например, при проведении
участком волокна (рис. 29) импульса слева направо
импульс сначала (в интервале х = О — х2) будет
ускоряться, затем (на интервале х = х2 — хъ) замедляться,
потом вновь ускоряться (на интервале х = хъ — Xj) и
затем замедляться до нормальной скорости (на интервале
X = Xj — ОО).
Такое воздействие на движущийся импульс может
привести к управлению моментом его прихода к соме,
управлению величиной вклада импульса в интегративные
процессы в разных участках рассматриваемого и других
волокон.
Если вектор возбуждения f будет меняться во времени,
то импульс будет ускоряться, замедляться либо
блокироваться в зависимости от текущего распределения ВПСП.
Наличие управляемых коэффициентов связи еще больше
расширяет возможности волокна по управлению
проведением возбуждения по нему.
2.3.3. Активные дендриты. Генерация импульсов
Если в активном волокне ВПСП в какой-либо точке
превысит порог h, то возникнет потенциал действия —
активный импульс (спайк). От точки возникновения
(обозначим ее х*) этот импульс начнет распространяться , по
волокну (дендриту) в обе стороны. Вследствие такого
распространения ВПСП, накопленный вблизи синапсов,
будет нейтрализован, т. е. волокно придет в равновесное
состояние и процесс сможет повторяться вновь. В
установившемся режиме в точке превышения порога возникнет
процесс генерации спайков с некоторой частотой v*.
Определим связь между вектором входного
возбуждения^, вектором выходного возбуждения g и частотой
генерации спайков в волокне v*. Пусть волокно генерирует
импульсы с частотой v* = \1Т. Учитывая
пространственную и временную суммацию в волокне, условие гене-
рации импульса в некоторой точке я* запишем в виде
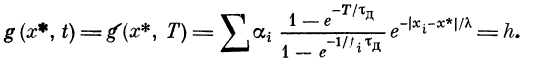
Здесь тд — постоянная времени рассасывания
деполяризации (ВПСП), at —- величина ВПСП вблизи i-ro синапса,
создаваемая одним пресинаптическим импульсом.
Величина at определяется из условия стремления g (х, t) в
асимптотике (при t-*~.oo) к величине ВПСП пассивного
дендрита:
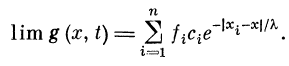
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
Отсюда
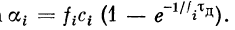
. Так как ощутимая
временная суммация возможна при условии

, то
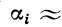
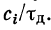
Следовательно,

где 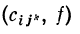 — скалярное произведение векторов
— скалярное произведение векторов 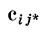 и f.
и f.
Частота генерации импульсов в активном волокне
пропорциональна величине среднего значения ВПСП в точке
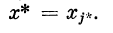
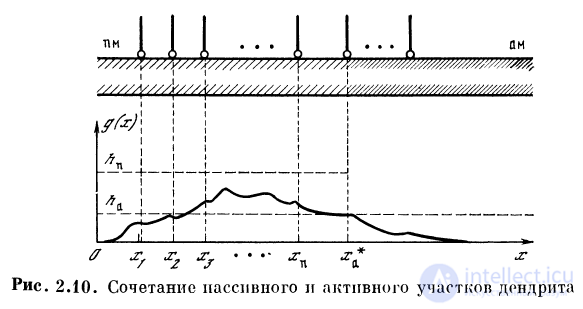
2.3.4. Сочетание пассивного и активного участков дендрита
Рассмотрим случай, когда синапсы расположены только
на пассивном участке дендрита, а активная часть
дендрита начинается в некоторой точке х = хА (рис. 2.10).
В этом случае активное возбуждение может возникнуть
в точке хА при условии 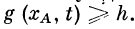 Проведя необходимые
Проведя необходимые
преобразования, получим для частоты генерации
импульсов в активном участке
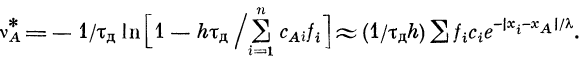
Частоту генерации импульсов v^ можно выразить через
скалярное произведение вектора входного возбуждения f
и вектора эффективных коэффициентов связей точки хА
с синапсами сг, с2, . . ., сп пассивной части волокна:
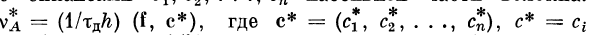
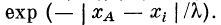
Аналогичная ситуация будет иметь
место в случае, когда пороги у двух отрезков волокон
различны. Тогда активный процесс будет возникать в отрезке
дендрита с меньшим порогом, так как в нем порог будет
превышаться раньше. Отличие будет лишь в том, что
активный процесс будет приводить в исходное состояние оба
отрезка волокна, а не только тот, в котором возник
импульс, как в случае сочетания пассивного и активного
участков.
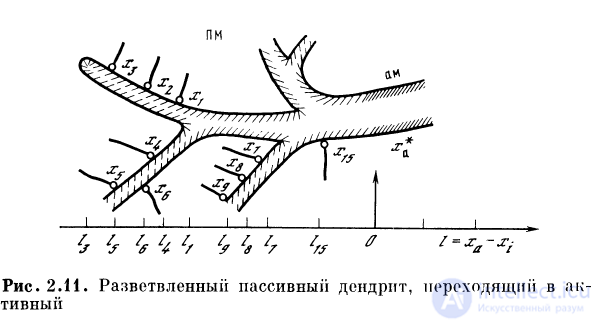
Пассивная часть волокна в рассматриваемом случае
может иметь произвольную конфигурацию (рис. 2.11).
Тогда в выражение для vA будут входить «эффективные»
константы длины и «эффективные» коэффициенты связи
синапсов с точкой активного участка: 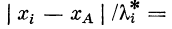
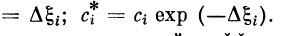
Каждое ответвление
характеризуется своей эффективной константой длины %i
и соответствующими ей эффективными коэффициентами
связей.
Рассмотрим дендритную систему, в которой пассивные
участки связаны с локальными активными участками,
разделенными участками невозбудимости (рис. 2.12). На ак-
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
тивных участках расположены дендро-дендритные
контакты с другими нервными элементами, к которым
поступают генерируемые в активных участках
последовательности спайков. Такая система может заменить собой целую
сеть из нейронов-сумматоров, функцию нейрона
выполняет здесь пассивное ответвление с локальным активным
участком, возбуждение которого передается через ден-
дро-дендритный контакт.
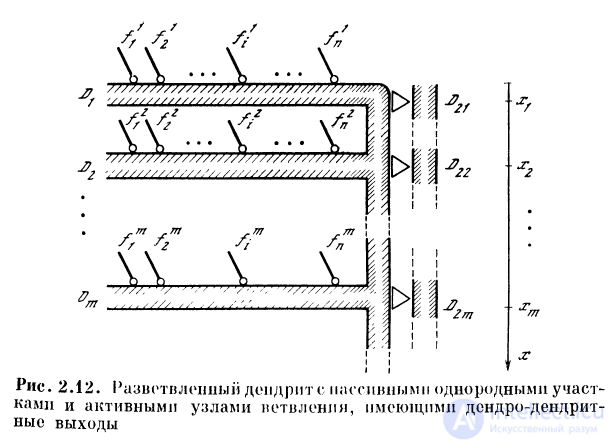
Дендритная система, в которой пассивные ответвления
входят в активный отрезок, может выполнять операцию
выделения максимума скалярных произведений
векторов возбуждения на вектора эффективных связей
ответвлений с точками входа их в активный участок
(рис. 2.13). Частота разрядов активного участка дендрита
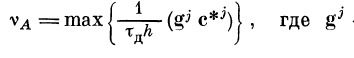 — вектор возбуждения
— вектор возбуждения
/-го ответвления, равный gj = || elk || fj — номер
ответвления дендрита, с*д — эффективный коэффициент связи
синапсов ответвлений с точками входа этих ответвлений
в активную зону — cV = с\ ехр (— | х{ — xj \ /Kj).
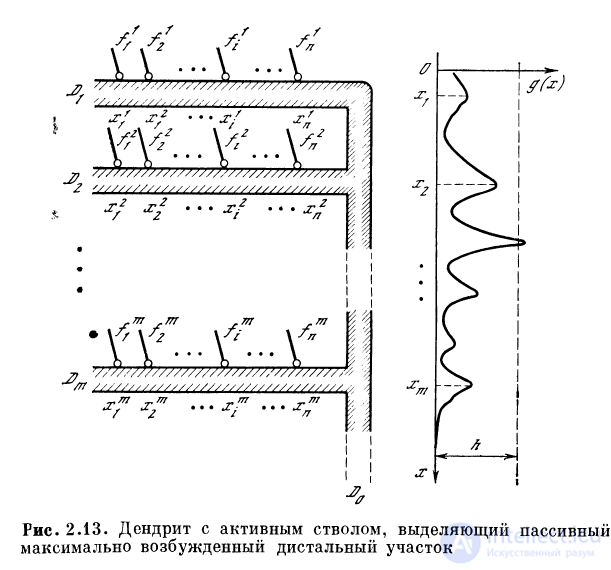
В реальных структурах могут существовать
произвольные комбинации активных и пассивных участков дендри-
тов, взаимодействие не только одномерных, но и двух-
и трехмерных многоуровневых дендритных структур,
в которых перекрещиванием дендритных волокон могут
детектироваться разнообразные характеристики процессов
возбуждения в сети. На рис. 2.14 показан пример
двумерной двухуровневой дендритной сети. На уровне Ьг —
в системе дендритов Дп, Д12, . ., Д1П — формируются
результаты разных преобразований. На L2 — системе
дендритов Д21, Д22,. • •» Дгп — формируются (в
зависимости от наборов коэффициентов дендро-дендритных
связей Z/j и L2) дендритные детекторы признаков разного
вида, которые могут нести информацию о результате
преобразований на Ьг.
2.3.5. Операция выделения максимума
из нескольких выходных сигналов
Входные сигналы — частоты следования импульсов.
Выходной сигнал пропорционален максимальной частоте
следования импульсов. Операция может быть реализована
на однородном дендрите активного типа, вдоль которого
на равных расстояниях друг от друга расположены
одинаковые синапсы. Механизм работы элемента следующий.
Импульс возникает в той точке дендрита, в которой
превышен порог. Затем импульсы, разделяясь на два,
распространяющихся в разные стороны, приводят все
волокно в активное состояние. Если все синапсы дендрита
одинаковые, то ВПСП около каждого из них будет
накапливаться тем быстрее, чем выше частота поступления пре-
синаптических импульсов. Очевидно, что порог превысится
раньше там, где частота поступления входных
импульсов выше. Таким образом, будет выделен максимальный
из приходящих сигналов. Чтобы не было влияния друг
на друга ВПСП от соседних синапсов, расстояния между
ними должны быть больше X. По окончании активного
возбуждения рассматриваемого участка волокна
деполяризация, накопленная около синапсов, уничтожится,
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
дендрит придет в исходное состояние и процесс сможет
повторяться. В итоге на выходе дендрита будут
появляться импульсы с частотой, пропорциональной
максимальной из поступающих на входы частот.
Этот результат следует из рассмотрения общего
выражения, связывающего частоту генерации спайков v
в дендрите с сигналами, поступающими к синапсам на
дендрите. Пусть fj = max {ft}. Тогда в точке Xj при
условии | xt — Xj | ^> К будут генерироваться импульсы
с частотой v (xj) : v (xj) = {тд1п [1 + (hiс) (1 — е17*1*)]"1}"1.
Таким образом выполняется функция непрерывной
логики «выделение максимума из нескольких величин».
2.3.6. Операция алгебраического суммирования
Названная операция реализуется при условиях
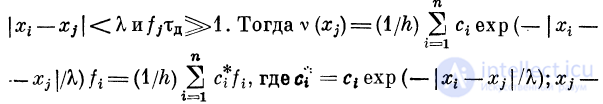
координата точки генерации спайков на дендрите
(точки, в которую приходит максимальный сигнал).
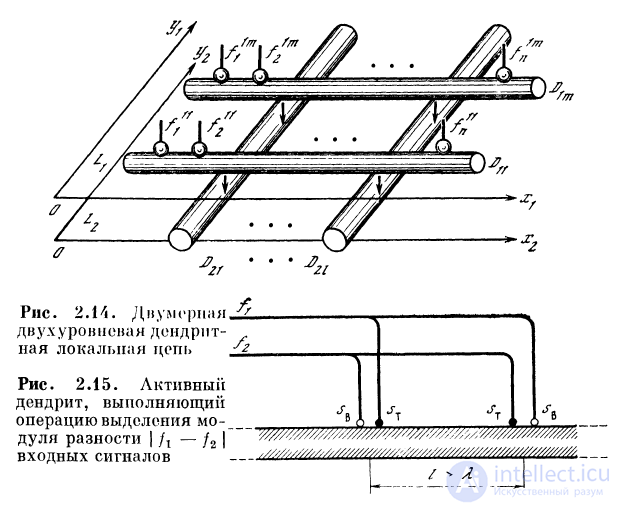
2.3.7. Операция выделения модуля разности
двух величин
К синапсам однородного дендрита поступают две
последовательности, различающиеся частотами следования спай-
ков. На выходе дендрита появляются спайки с частотой,
пропорциональной модулю разности сигналов. Для этого
каждая входная последовательность подается на
возбуждающий и тормозной синапсы, расположенные на
расстоянии, большем X. Возбуждающий синапс первого входного
сигнала расположен вблизи от тормозного синапса, на
который поступает второй входной сигнал, и наоборот
(рис. 2.15). Вследствие такой организации связей ВПСП
от одного сигнала суммируются с ТПСП другого. При
разных входных частотах вблизи возбуждающего синапса,
на который приходит меньший сигнал, будет нарастать
гиперполяризация за счет того, что вследствие временной
суммации ТПСП больше ВПСП. В результате порог
возбуждения будет превышаться лишь вблизи
возбуждающего синапса, на который приходит больший сигнал. Время
нарастания суммарной деполяризации до порога
обратно пропорционально модулю разности частот следования
входных импульсов. Поэтому частота следования
возникающих в дендрите спайков будет пропорциональна
модулю разности входных сигналов.
2.3.8. Операция выделения частоты следования
импульсов
Пусть к двум входным ответвлениям узла подходят две
коллатерали одного и того же аксона. Синапсы в местах
соединений отстоят от узла на разных расстояниях: время
проведения от одного из них на интервал т меньше, чем
от другого. Узел выполняет операцию совпадения.
Совпадать в узле будут импульсы, возникающие вблизи
синапсов через интервал т или через т/тг, где п — целое число.
В результате дендритный узел будет играть роль
«полосового фильтра» частоты следования входных импульсов.
Допустимая задержка во времени прихода одного из
импульсов Д^шах = тд1п {g2l{h — g2)). Пусть координаты
синапсов с1 и с2 (расстояния от точки ветвления узла)
равны соответственно х1 и х2. Тогда при условии

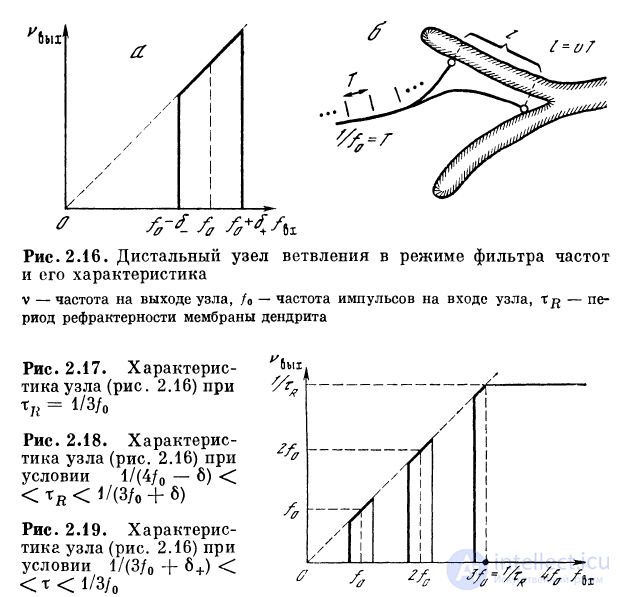
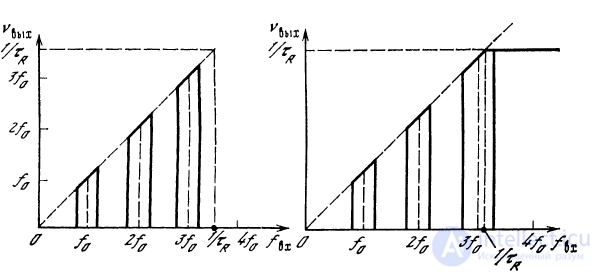
т. е. тогда, когда запаздывающий импульс приходит в узел
в момент прихода туда п + 1-го импульса от синапса,
расположенного ближе к узлу. Таким образом, п
импульсов будет блокировано в узле, а все последующие будут
проходить. Если рассматривается реальное разветвление,
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
то условие (2) будет иметь вид

Рассматриваемое разветвление представляет собой
«детектор мгновенной частоты» следования входных
импульсов (здесь v — скорость распространения возбуждения по
дендриту).
Полосовой фильтр с узкой полосой пропускания может
быть получен при следующих условиях:

В неравенстве (5) /0 определяется из формулы (2) при h =
= 1, %r — рефрактерный период. Характеристика такого
фильтра показана на рис. 2.16. Здесь
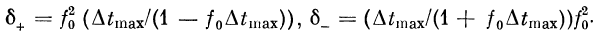
Учитывая соотношение (4), получим 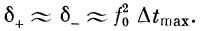
Итак, полоса пропускания такого фильтра будет

В зависимости от того, как связаны рефрактерный
период Xr и минимальная пропускаемая узлом частота
/0 = vl | х2 — х1 , характеристики узла будут иметь
разный вид. Например, при выполнении условия
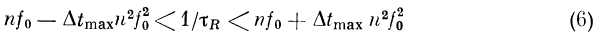
характеристика будет иметь п полос пропускания
(рис. 2.17), причем последняя будет простираться от f = 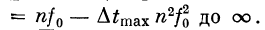
При условии
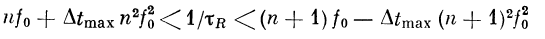
будет иметься л полос пропускания, каждая шириной
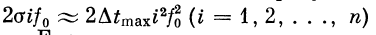 (рис. 2.18).
(рис. 2.18).
Если, начиная с некоторого /г, выполняется условие
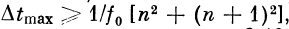 то характеристика будет
то характеристика будет
иметь вид, как на рис. 2.19.
Electron in the transistor-resistor kingdom
Game: Perform tasks and rest cool.7 people play!
Play game
2.3.9. Нейронная сеть, выделяющая определенную
частоту следования входных импульсов
То есть имеется в виду сеть, элементы которой в силу
определенной организации связей становятся селективными
детекторами частот следования импульсов. При
поступлении на общий вход сети последовательности импульсов
с частотой / (I) в сети возбуждается лишь тот нейрон, для
которого данная частота является «своей». Структура сети
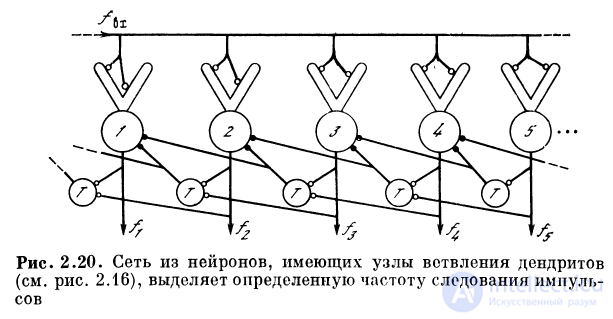
показана на рис. 2.20. Нейроны с дендритами, имеющими
на конце настроенный на определенную частоту
пропускания импульсов узел ветвления, расположены в порядке
возрастания их основных «резонансных» частот. Между
чувствительными к частоте следования импульсов
нейронами располагаются тормозные нейроны — аналоговые
сумматоры.
Механизм работы сети следующий. Если для
некоторого нейрона номер i выполнено условие \f(t) — ft | <
<8(fi), то этот нейрон будет возбужден через время
Д^ = IIfi и через тормозной нейрон начнет тормозить
расположенные слева от него нейроны, настроенные на более
низкие частоты. Нейроны, настроенные на частоты,
меньшие f^ могли бы возбудиться через время, большее
А^, так как Atj = l/fj > 1//ь где / = 1,2,..., i — 1.
Однако тормозное воздействие от нейрона i приходит к ним
раньше, чем они успеют возбудиться. Нейроны,
настроенные на более высокие частоты, вообще не будут
возбуждены. В результате на выходе сети будет возбужден
только один элемент — детектор частоты следования входных
импульсов.
Рассматриваемая сеть достаточно экономна, так как
при любой частоте на входе в сети будут возбуждены лишь
два нейрона: настроенный на данную частоту «детектор»
и связанный с ним тормозной нейрон. Остальные
нейроны либо находятся в заторможенном состоянии, либо не
возбуждены из-за «резонансных» свойств их узлов
ветвления.
Сеть имеет большую надежность, так как при выходе
из строя какого-либо из нейронов сети, например /-го,
его функцию «берет» на себя расположенный слева от
него (/ — 1)-й нейрон. При этом «разрешающая
способность» сети уменьшится, потому что нейрон, заменяющий
вышедший из строя, будет отвечать на частоты в двух
полосах , чего при исправной работе сети быть не должно. Потеря
детектора может быть скомпенсирована, так как
частота на выходе (/ — 1)-го нейрона при ответе на «не свою»
частоту станет больше, чем она может быть в
неповрежденной сети. Это обстоятельство может служить сигналом
в верхние уровни о неисправности нейрона и
необходимости замены его каким-либо резервным элементом,
например, следующего уровня.
Анализ данных, представленных в статье про информационные процессы в дендритных структурах , подтверждает эффективность применения современных
технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое информационные процессы в дендритных структурах
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Нейробионика

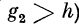
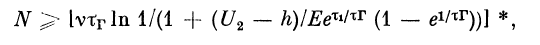
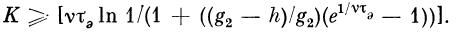
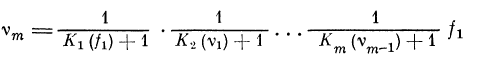
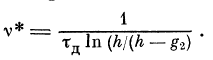
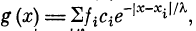 , где i = 1, 2, . . ., гг. Обозначим
, где i = 1, 2, . . ., гг. Обозначим 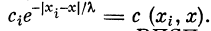 . Коэффициент
. Коэффициент 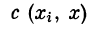
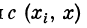 функцией связи точки xt
функцией связи точки xt 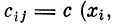
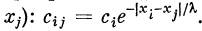 . Коэффициенты связей Сц представим
. Коэффициенты связей Сц представим 
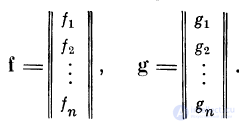
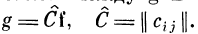
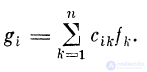


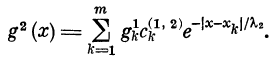
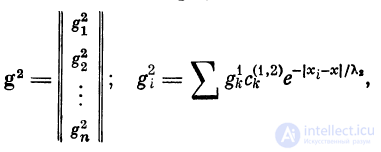
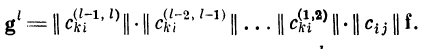
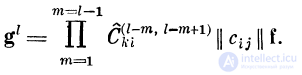
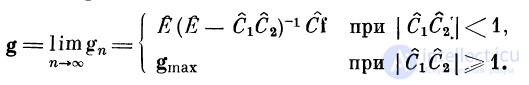
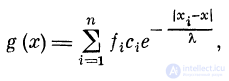
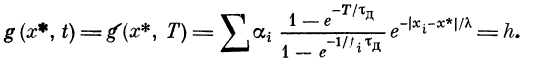
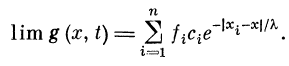
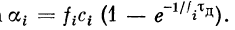 . Так как ощутимая
. Так как ощутимая  , то
, то 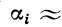
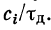

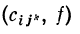 — скалярное произведение векторов
— скалярное произведение векторов 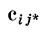 и f.
и f. 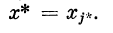
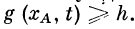 Проведя необходимые
Проведя необходимые 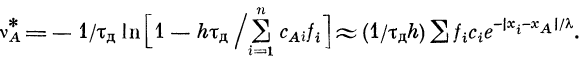
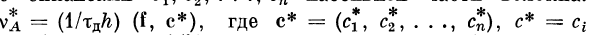
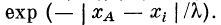
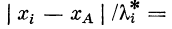
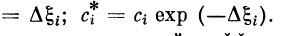


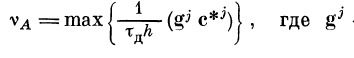 — вектор возбуждения
— вектор возбуждения 


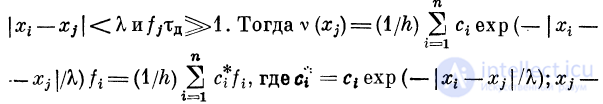





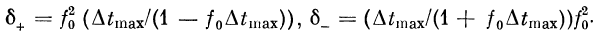
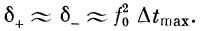

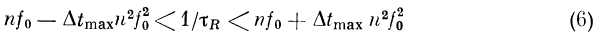
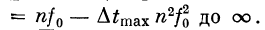
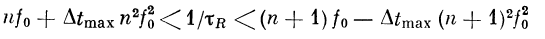
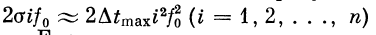 (рис. 2.18).
(рис. 2.18). 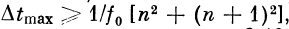 то характеристика будет
то характеристика будет 
Комментарии
Оставить комментарий
Нейробионика
Термины: Нейробионика