Тангенциальный - понятие и значение

Рассмотрим что означает понятие и значение слова тангенциальный (информация предоставлена intellect.icu).

1. прилагательное Направленный по касательной к данной кривой (в математике).

1. Тангенциальная, тангенциальное (от латинское tangens - касающийся) ( математика ). Направленный по касательной к данной кривой. Тангенциальная линия.

Спец.

Направленный по касательной к данной кривой.

Тангенциальное направление. Тангенциальное давление. Тангенциальный распил бревна.

{От лат. tangens, tangentis — касающийся}

Часть речи

Имя прилагательное (полное)

Словоформы

тангенциального, тангенциальному, тангенциальным, тангенциальном, тангенциальная, тангенциальной, тангенциальную, тангенциальною, тангенциальное, тангенциальные, тангенциальных, тангенциальными

Синонимы

касательный

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "тангенциальный":
абажурный, абактинальный, абдикационный, абдоминальный, аберрационный, абинный, абиогенный, абиссальный, абнормальный, абонементный, боскетный, голосемянный, званый, малосемейный, несравненный, полубольный, хлебный, чебуречный, швейный

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "тангенциальный" :
сенотиный, толориный, вановуный, лоневоный, тытаконый, тощигиный, кярочыный, касодиный.


Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Тангенциальный" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Т525, для metaphone-"тангинциалнaй" и для double-metaphone primary : TNJN secondary: TNKN.

См. также

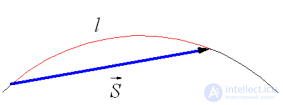... изменяется , а изменяется только направление скорости Изменение величины скорости за единицу времени – это тангенциальное ускорение :. или Где vτ, – величины скоростей в момент времени + Δt. и Тангенциальное ускорение в данной точке ... ... вектор изменения скорости равен векторной сумме двух векторов .: По определению : Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению . и направлена по касательной ... (Физические основы механики)

... этой задачи кроме, распределение источников впространстве ., необходимо знать также граничные условия длятангенциальных компонент электрического либо .магнитного поля награницах рассматриваемой области (еслионисуществуют ).Вместе ... ... из.1 вВместе стем, мы можем формально наэтой поверхности .написать граничные условия длятангенциальных компонент поля Длятангенциальной компоненты магнитного поля граничное условие длянапряженности магнитного ... (Теория электромагнитного поля)

... производной вектора по времени t, или, что то. же самое - второй производной по времени радиус-вектора :. Рис Тангенциальное и нормальное ускорения Если известны зависимость от времени ускорения а = a(t) и. начальная скорость (при t = ), то значение ... ... взаимно ортогональных . составляющих , обозначем их и :. Обсудим физический смысл каждого слагаемого Слагаемое - это тангенциальное ускорение , которое характеризует быстроту изменения модуля скорости Эта часть полного ... (Физические основы механики)

... ускорения точек вращающегося тела Нормальное ускорение : подставляя значение скорости из , находим :. Тангенциальное ускорение Воспользовавшись тем же отношением получаем Таким образом , как нормальное , так и, тангенциальное ускорения ... (Физические основы механики)

... скорости Ускорение точки тела при вращении может быть представлено как геометрическая . сумма тангенциального и нормального ускорения причем тангенциальное ускорение получается как производная от алгебраической скорости точки ... (Физические основы механики)

... Согласно второму закону Ньютона , для тангенциальной составляющейсилы , действующей на материальную . точку массой m, и ускорения . можем записать С учетом , что и имеем ... (Физические основы механики)

---

---