Конус - понятие и значение

Рассмотрим что означает понятие и значение слова конус (информация предоставлена intellect.icu).

1. Геометрическое тело, образуемое вращением прямоугольного треугольника вокруг одного из его катетов (в математике).
2. То, что формой напоминает такое геометрическое тело.

1. Геометрическое тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов. 2.Предмет такой формы.К. террикона.

1. Конуса, ( греческое konos). 1. Геометрическое тело, создаваемое вращением прямоугольного треугольника вокруг одного из катетов ( математика ).
2. Всякое физическое тело, близкое по форме геометрическому конусу. Предо мной свой белый конус ты высишь, снежный Арарат! Брю совершенный вид 2. Один из видов механизма сцепления в автомобиле, служащий для передачи движения от мотора к задним колесам ( техника ).

КОНУС

(лат. conus; греческое konos). Тело, ограниченное поверхностью, образующейся от обращения прямой, коей один конец неподвижен (вершина конуса), а другой двигается по окружности данной кривой; с виду похож на сахарную голову.

КОНУС

геометрическое тело, ограниченное кривою поверхностью, сходящеюся в одной точке, и плоскостью круга, которая называется основанием к. (Сахарная голова может дать понятие о форме к.).

КОНУС

лат. conus, греческое konos. Тело, описываемое треугольником, движущимся около одной из своих сторон.

КОНУС

тело, ограниченное кривою поверхностью, сходящеюся в одной точке (вершина), и плоским кругом, который принимается за основание. Получается от вращения прямоугольного треугольника вокруг одного из катетов.

-а, м.

1.

Геометрическое тело, образуемое вращением прямоугольного треугольника вокруг одного из катетов.

Боковая поверхность конуса.

2. обычно чего.

Предмет или его часть (обычно верхняя), имеющие такую форму, а также то, что насыпано, уложено и так далее в виде такой формы.

Первоначальный конус Авачинского вулкана разрушен давно ---. Нынешний конус насыпан далеко не до прежних размеров. Арсеньев, Восхождение на Авачинский вулкан.

Тяжелой струей хлынуло {из бункера} зерно. На земле начал быстро расти правильный желтый конус. С. Антонов, Поддубенские частушки.

{Греч. κω̃νος}

Часть речи

Имя существительное

Словоформы

конуса, конусу, конусом, конусе, конусы, конусов, конусам, конусами, конусах

Синонимы

тело, моллюск, зандр, сфероконус, отложение, пустошь, шатер, горнитос, пролювий

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "конус":
аденостефанус, алумнус, анус, атроспогнус, бурнус, гамбринус, ганус, гепатогнус, гнус

Рифмы для этого же слова "конус", но если ударение на последний слог :
абакус, абельмошус, абрус, автобус, аденовирус.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "конус" :
нарабюнус, бурепонус, сеыиренус, ресотунус, гитибунус, далосинус, тонезанус, меназонус.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Конус" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-К520, для metaphone-"кaнус" и для double-metaphone KNS.

См. также

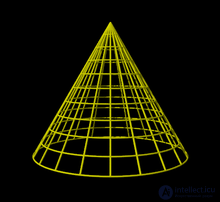
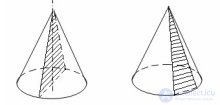... через его вершину , представляет собой равнобедренный . треугольник , у которого боковые стороны являются образующими конуса В частности , равнобедренным треугольником является осевое сечение конуса Теорема Плоскость ., параллельная плоскости ... ... , равнобедренным треугольником является осевое сечение конуса Теорема Плоскость ., параллельная плоскости основания конуса , пересекает конус по кругу , а боковую .поверхность – по окружности с центром на оси конуса Доказательство ... (Стереометрия)

... из круга – основания конуса , точки ., не лежащей в плоскости этого круга , - вершины конуса и всех .отрезков , соединяющих вершину конуса с точками основания Отрезки , соединяющие вершину ... ... лежащей в плоскости этого круга , - вершины конуса и всех .отрезков , соединяющих вершину конуса с точками основания Отрезки , соединяющие вершину конуса с точками окружности основания , называются ... (Стереометрия)

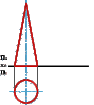... Построение тени конуса на эпюре ... (18 Тени и отражения)

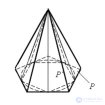... Построим два многоугольника в плоскости основания конуса : многоугольник P, содержащий . основание конуса , и многоугольник P`, содержащийся в основании конуса Построим две пирамиды с основаниями P и P` и вершиной . в вершине ... ... , и многоугольник P`, содержащийся в основании конуса Построим две пирамиды с основаниями P и P` и вершиной . в вершине конуса Первая пирамида содержит конус , а вторая пирамида содержится в конусе . Существуют такие многоугольники ... (Стереометрия)

... конуса . и перпендикулярная плоскости осевого сечения , содержащей эту образующую Пирамида , описанной около конуса , называется пирамида , у которой основанием служит . многоугольник , описанный около основания конуса , а вершина ... ... конуса . и перпендикулярная плоскости осевого сечения , содержащей эту образующую Пирамида , описанной около конуса , называется пирамида , у которой основанием служит . многоугольник , описанный около основания конуса , а вершина ... (Стереометрия)

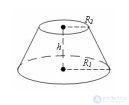... Пусть есть усеченный конус с радиусами оснований и. ( ... (Стереометрия)

---

---