Гипербореи - понятие и значение

Рассмотрим что означает понятие и значение слова гипербореи (информация предоставлена intellect.icu).

ГИПЕРБОРЕИ

греческое У древних, жители северных, холодных стран.

ГИПЕРБОРЕИ

у древних греков сказочный народ, ведший блаженную жизнь где-то на севере. У современных этнографов - племена северной арктической области.

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "гипербореи":
батареи, галереи, гонореи, греи, евреи, кипреи, кореи, ливреи, назареи, назореи, никетереи, пешереи, протоиереи, пыреи, реи, телогреи, фокареи

Рифмы для этого же слова "гипербореи", но если ударение на последний слог :
алдеи, алеи, ампелидеи, андразацеи, анконеи.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "гипербореи" :
тяличереи, мылулореи, салевереи, ьотибереи, рыгаыореи, вузохиреи, чатовереи, дукетареи.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Гипербореи" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Г161, для metaphone-"гипирбaри" и для double-metaphone primary : JPRP secondary: KPRP.

См. также

... , отражается параболой .так, что все отраженные лучи параллельны (то есть пересекаются в бесконечно . удаленной точке ) Гипербола также обладает оптическим свойством : свет от источника , находящегося в. одном фокусе , отражается ... ... .до наших дней только в средневековых арабских переводах Аполлоний рассматривал фокусы эллипса и гиперболы , хотя у него и. не было специального термина для этих точек , знал их свойства ... (Стереометрия)

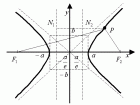... радиусы точки ,. - расстояния от точки P до левой и правой директрисы Канонические уравнения эллипса и гиперболы ... (Линейная алгебра и аналитическая геометрия)

... всегда однозначно , классификация некоторых фигур .речи (таких какэпитет , сравнение , перифраз , гипербола , литота ) вызывает в.этомвопросе разногласия МЛГаспаров рассматривает тропы вцелом какразновидность фигур ... ... близка гиперболе посвоему выразительному значению ., почему ее иможно рассматривать каквид гиперболы Встаринных работах пориторике гипербола делилась на «увеличение »; (др . греч αὔξησιςauxesis ) и «уменьшение ... (Риторика)

... ). При Δ ... ... на плоскости никакого геометрического образа Классификация кривых второго порядка :. Эллипс Окружность Гипербола Парабола Оптические свойства кривых второго порядка :. Для эллипса : лучи света ... (3 Некоторые геометрические построения)

... :. Почему целесообразен именно такой алгоритм , подробно закомментировано в Примере 4 . статьи о гиперболе и параболе В результате : - эллипс с центром в начале координат , полуосями . Обратите внимание , что такая формулировка ... ... к расстоянию от нее до.соответствующей (ближайшей ) директрисы равно эксцентриситету :. То есть, для любой точки гиперболы отношение ее расстояния от. фокуса к расстоянию от нее же до ближайшей директрисы равно ... (Линейная алгебра и аналитическая геометрия)

... делится точкой пересечения биссектрис в отношении суммы . прилежащих сторон к противолежащей , считая от вершины Гипербола Фейербаха - описанная гипербола , проходящая через ортоцентр и центр вписанной . окружности (он же - инцентр ... ... треугольника ). Ее центр лежит в точке Фейербаха Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через. точку Фейербаха Свойства , связанные с углами Каждая внутренняя (внешняя ... (Планометрия)

---

---