1. Стилистический прием, заключающийся в чрезмерном преувеличении каких -либо качеств или свойств изображаемого предмета, явления и тому подобное с целью усиления впечатления.
2. разговорное Любое чрезмерное преувеличение. 2. Незамкнутая кривая из двух ветвей, получаемая при пересечении обеих плоскостей поверхности кругового конуса плоскостью, не проходящей через его вершину (в геометрии).
В поэтике: слово или выражение, заключающее в себе преувеличение для создания художественного образа; вообще - преувеличение.
1. Гиперболы, ( греческое hyperbole). 1. Кривая из числа конических сечений ( математика ). Гипербола получается при сечении прямого круговорота конуса плоскостью. 2. Фигура преувеличения (л (итальянское) ). Стиль Гоголя изобилует гиперболами.
2. Всякое чрезмерное, преувеличенное высказывание по поводу чего кто-нибудь ( книжное ). Ну, это гипербола: в действительности всё происходило проще.
ГИПЕРБОЛА
( греческое , hyperbole, от hyperballein - бросать далее цели). 1) в геометрии: две кривые линии, получаемые при пересечении конуса плоскостью, параллельной оси конуса. 2) в риторике: выражение мысли в сильно преувеличенной форме для большей силы впечатления, например море слез.
ГИПЕРБОЛА
1) преувеличение, выходящее из пределов вероятного и возможного; 2) в математике: кривая линия, получающаяся при пересечении конуса плоскостью параллельной его оси.
ГИПЕРБОЛА
греческое hyperbole, от hyperballein, бросать далее цели. а) Преувеличение. b) Кривая линия, получаемая от сечения конуса.
ГИПЕРБОЛА
преувеличение; также кривая, образуемая пересечением конуса параллельной его оси плоскостью.
(1)
-ы, женский род
Стилистический прием чрезмерного преувеличения каких -либо свойств изображаемого предмета, явления и так далее , с целью усиления впечатления.
Всякое чрезмерное преувеличение.
С вами я отводил душу — это не гипербола, а сущая правда. Белинский, Письмо И. С. Тургеневу, 8 июля 1843.
{От греческое ‛υπερβολή — преувеличение}
(2)
-ы, женский род Мат.
Несомкнутая кривая из двух ветвей, получаемая при пересечении конуса плоскостью.
{От греческое ‛υπερβάλλω — прохожу через что -либо }

 ... , отражается параболой .так, что все отраженные лучи параллельны (то есть пересекаются в бесконечно . удаленной точке ) Гипербола также обладает оптическим свойством : свет от источника , находящегося в. одном фокусе , отражается ... ... .до наших дней только в средневековых арабских переводах Аполлоний рассматривал фокусы эллипса и гиперболы , хотя у него и. не было специального термина для этих точек , знал их свойства ... (Стереометрия)
... , отражается параболой .так, что все отраженные лучи параллельны (то есть пересекаются в бесконечно . удаленной точке ) Гипербола также обладает оптическим свойством : свет от источника , находящегося в. одном фокусе , отражается ... ... .до наших дней только в средневековых арабских переводах Аполлоний рассматривал фокусы эллипса и гиперболы , хотя у него и. не было специального термина для этих точек , знал их свойства ... (Стереометрия)
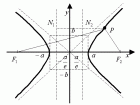 ... радиусы точки ,. - расстояния от точки P до левой и правой директрисы Канонические уравнения эллипса и гиперболы ... (Линейная алгебра и аналитическая геометрия)
... радиусы точки ,. - расстояния от точки P до левой и правой директрисы Канонические уравнения эллипса и гиперболы ... (Линейная алгебра и аналитическая геометрия)
 ... всегда однозначно , классификация некоторых фигур .речи (таких какэпитет , сравнение , перифраз , гипербола , литота ) вызывает в.этомвопросе разногласия МЛГаспаров рассматривает тропы вцелом какразновидность фигур ... ... близка гиперболе посвоему выразительному значению ., почему ее иможно рассматривать каквид гиперболы Встаринных работах пориторике гипербола делилась на «увеличение »; (др . греч αὔξησιςauxesis ) и «уменьшение ... (Риторика)
... всегда однозначно , классификация некоторых фигур .речи (таких какэпитет , сравнение , перифраз , гипербола , литота ) вызывает в.этомвопросе разногласия МЛГаспаров рассматривает тропы вцелом какразновидность фигур ... ... близка гиперболе посвоему выразительному значению ., почему ее иможно рассматривать каквид гиперболы Встаринных работах пориторике гипербола делилась на «увеличение »; (др . греч αὔξησιςauxesis ) и «уменьшение ... (Риторика)
 ... ). При Δ ... ... на плоскости никакого геометрического образа Классификация кривых второго порядка :. Эллипс Окружность Гипербола Парабола Оптические свойства кривых второго порядка :. Для эллипса : лучи света ... (3 Некоторые геометрические построения)
... ). При Δ ... ... на плоскости никакого геометрического образа Классификация кривых второго порядка :. Эллипс Окружность Гипербола Парабола Оптические свойства кривых второго порядка :. Для эллипса : лучи света ... (3 Некоторые геометрические построения)
 ... :. Почему целесообразен именно такой алгоритм , подробно закомментировано в Примере 4 . статьи о гиперболе и параболе В результате : - эллипс с центром в начале координат , полуосями . Обратите внимание , что такая формулировка ... ... к расстоянию от нее до.соответствующей (ближайшей ) директрисы равно эксцентриситету :. То есть, для любой точки гиперболы отношение ее расстояния от. фокуса к расстоянию от нее же до ближайшей директрисы равно ... (Линейная алгебра и аналитическая геометрия)
... :. Почему целесообразен именно такой алгоритм , подробно закомментировано в Примере 4 . статьи о гиперболе и параболе В результате : - эллипс с центром в начале координат , полуосями . Обратите внимание , что такая формулировка ... ... к расстоянию от нее до.соответствующей (ближайшей ) директрисы равно эксцентриситету :. То есть, для любой точки гиперболы отношение ее расстояния от. фокуса к расстоянию от нее же до ближайшей директрисы равно ... (Линейная алгебра и аналитическая геометрия)
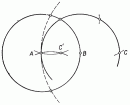
 ... делится точкой пересечения биссектрис в отношении суммы . прилежащих сторон к противолежащей , считая от вершины Гипербола Фейербаха - описанная гипербола , проходящая через ортоцентр и центр вписанной . окружности (он же - инцентр ... ... треугольника ). Ее центр лежит в точке Фейербаха Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через. точку Фейербаха Свойства , связанные с углами Каждая внутренняя (внешняя ... (Планометрия)
... делится точкой пересечения биссектрис в отношении суммы . прилежащих сторон к противолежащей , считая от вершины Гипербола Фейербаха - описанная гипербола , проходящая через ортоцентр и центр вписанной . окружности (он же - инцентр ... ... треугольника ). Ее центр лежит в точке Фейербаха Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через. точку Фейербаха Свойства , связанные с углами Каждая внутренняя (внешняя ... (Планометрия)
Комментарии
Оставить комментарий