то же, что бортовая качка ( смотри бортовой).
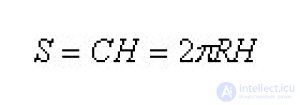... n периметр Pn неограниченно приближается к длине . С окружности основания цилиндра Следовательно , площадь боковой поверхности призмы неограниченно приближается к CH Поэтому величина CH принимается за площадь ... (Стереометрия)
... приближается к. длине С окружности основания конуса , а апофема ln – к длине .l образующей Соответственно боковая поверхность пирамиды неограниченно приближается к В связи с этим величина 0, принимается за площадь . боковой ... ... конуса вычисляется по формуле где R – радиус . основания конуса , а l – длина образующей Для площади боковой поверхности усеченного конуса с радиусами оснований ., и образующей l получается формула ... (Стереометрия)
... ,. будет иметь сдвиг по фазе , если при прохождении через оптическое . волокно спектр оптической несущей или боковой полосы подавляется в спектре усиления . ВБР Недостатком данной схемы является дорогостоящая и технически ... ... сигнал . лазера поступает на фазовый модулятор , на выходе которого формируется несущая и две боковые составляющие Следует отметить , что боковые составляющие не совпадают по фазе Таким образом ... (Устройства СВЧ и антенны)
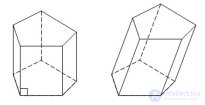... Призма называется прямой , если ее боковые ребра перпендикулярны основаниям Призма называется наклонной , если ее боковые ребра не перпендикулярны основаниям . У прямой призмы грани – прямоугольники Призма называется ... ... грани – прямоугольники Призма называется правильной , если ее основания являются правильными многоугольниками Площадью боковой поверхности призмы называется сумма площадей боковых граней Полная поверхность призмы ... (Стереометрия)
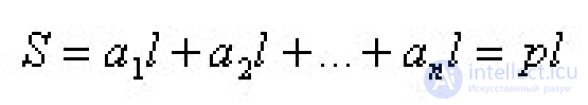... поверхность прямой призмы равна произведению периметра основания на. высоту призмы , т е на длину бокового ребра Доказательство Боковые грани прямой призмы – прямоугольники Основания этих прямоугольников ... ... прямоугольников являются сторонами многоугольника , лежащего в основании призмы ., а высоты равны длине боковых ребер Следовательно , боковая поверхность призмы равна где , , …, an – длины . ребер основания , p – периметр ... (Стереометрия)
... Боковой поверхностью пирамиды называется сумма площадей ее боковых граней Теорема Боковая поверхность правильной пирамиды равна произведению полупериметра основания на. апофему Доказательство Если ... ... произведению полупериметра основания на. апофему Доказательство Если сторона основания a, число сторон n, то боковая . поверхность пирамиды равна : где l – апофема , p – периметр основания пирамиды Теорема доказана ... (Стереометрия)
Комментарии
Оставить комментарий