5. Волны мозга

Привет, мой друг, тебе интересно узнать все про волны мозга, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое волны мозга , настоятельно рекомендую прочитать все из категории Логика мышления.

 

Итак, мы подошли к описанию одного из ключевых принципов описываемой модели. Этот принцип ранее не использовался ни в нейронных сетях, ни при описании работы мозга. В связи с этим я крайне рекомендую ознакомится с предыдущими частями. Как минимум необходимо прочитать четвертую часть без которой описанное ниже, будет совершенно непонятно.

В предыдущей части мы говорили о том, что активность нейронов делится на вызванную и фоновую. Отголоски фоновой активности наблюдают, снимая электроэнцефалограмму. Записываемые сигналы имеют сложную форму и зависят от места приложения электродов к голове, но, тем не менее, в них достаточно четко прослеживаются отдельные гармонические составляющие.

Основные ритмы получили названия:

• альфа-ритм (от 8 до 13 Гц);
• бета-ритм (от 15 до 35 Гц);
• гамма-ритм (от 35 до 100 Гц);
• дельта-ритм (от 0,5 до 4 Гц);
• тэта-ритм (от 5 до 7 Гц);
• сигма-ритм «веретена» (от 13 до 14 Гц).

Природу ритмов традиционно принято соотносить с осциляторными свойствами нейронов. Так, поведение одиночного нейрона описывается уравнениями Ходжкина-Хаксли (Hodgkin, 1952):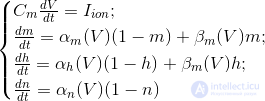




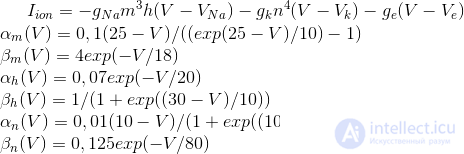
Эти уравнения определяют автоволновой процесс, то есть предписывают нейрону генерировать импульсы. Модель Ходжкина-Хаксли сложна для моделирования. Поэтому существует достаточно много ее упрощений, сохраняющих основные генерирующие свойства. Наиболее популярные модели: Фитцхью-Нагумо (Fitzhugh, 1961), Моррис-Лекара (Morris C., Lecar H., 1981), Хиндмарш-Роуз (Hindmarsh J. L., and Rose R. M., 1984). Многие модели, например, Хиндмарш-Роуз позволяют смоделировать как пачечную активность, так и обособленные спайки (рисунок ниже).


Пачечная активность и спайки, возникающие при моделировании нейрона Хиндмарш-Роуз

Объединяя нейроны, генерирующие собственные импульсы, в конструкции, напоминающие строение реальной коры, удается воспроизвести различные эффекты, характерные для групповой активности реальных нейронов. Например, можно добиться глобальной синхронизации нейронной активности или вызвать появление волн. Наиболее известные модели: Вилсона-Кована (H.R. Wilson and J.D. Cowan, 1972) и Куромото (Kuramoto, 1984).

Электроэнцефалограмма фиксирует отголоски совместной активности нейронов, но понятно, что у этой активности есть определенная пространственно-временная организация. Методы оптического наблюдения за активностью коры позволяют увидеть ее в живую. У подопытного животного обнажают участок коры и вводят специальный краситель, чувствительный к изменениям электрического потенциала. Под воздействием суммарных колебаний мембранного потенциала нейронов такой краситель меняет свои спектральные свойства. И хотя эти изменения крайне малы, они, тем не менее, могут быть зафиксированы, например, с помощью диодного массива, выполняющего роль высокоскоростной видеокамеры. Оптические методы не позволяют заглянуть вглубь коры и проследить активность отдельных нейронов, но они дают возможность составить общее представление о течении волновых процессов на ее поверхности.


Схема оптической фиксации активности коры (Michael T. Lippert, Kentaroh Takagaki, Weifeng Xu, Xiaoying Huang, Jian-Young Wu, 2007)

Оказалось, что ритмам мозга соответствуют волны, возникающие в точечных источниках и распространяющиеся по коре, как круги по воде. Правда, фронт волны на воде расходится строго по кругу, а фронт волны активности нейронов мозга может распространяться более сложным образом. На рисунке ниже показаны картины распространения волн на 5 миллиметровом участке коры мозга крысы.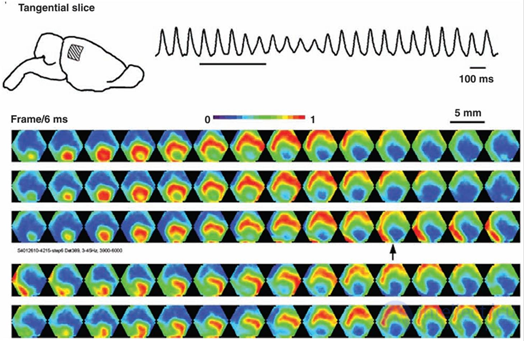


Картина распространения волны активности на участке коры мозга крысы. Потенциал показан градиентом от синего к красному. 14 кадров с интервалом 6 миллисекунд покрывают один цикл распространения волны (84 миллисекунды – 12 Гц) (Michael T. Lippert, Kentaroh Takagaki, Weifeng Xu, Xiaoying Huang, Jian-Young Wu, 2007)

Очень интересные и показательные видеозаписи волновой активности приведены в работе (W.-F. Xu, X.-Y. Huang, K. Takagaki, and J.-Y. Wu, 2007). Там показано, что волны могут уплотняться, доходя до границы зоны коры, могут отражаться от другой зоны и создавать встречную волну, могут распространяться двойными спиралями и создавать вихри.


Компрессия и отражение волны в первичной зрительной коре (W.-F. Xu, X.-Y. Huang, K. Takagaki, and J.-Y. Wu, 2007)

Ниже видео из той же работы (W.-F. Xu, X.-Y. Huang, K. Takagaki, and J.-Y. Wu, 2007):

 

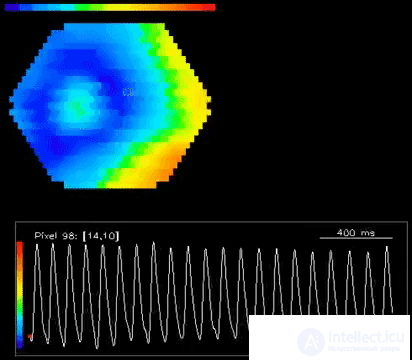
Используя модели осциллирующих нейронов, можно и в компьютерных экспериментах получить аналогичные волновые картины. Но сама по себе такая пульсация не несет большого смысла. Вполне разумно предположить, что волны активности – это механизм переноса и обработки информации. Но попытки в традиционных моделях объяснить природу этого механизма не дали ощутимых результатов. Кажется логичным допустить, что информация кодируется частотными и фазовыми характеристиками нейронных сигналов. Но это приводит к необходимости учитывать интерференционные процессы и ставит больше вопросов, чем вносит ясности.

Существует гипотеза, что волны «сканируют» кору, считывая с нее информацию для последующей ее передачи (Pitts W., McCulloch W.S., 1947). Это выглядит достаточно здраво, по крайней мере, относительно альфа-волн и первичной зрительной коры. Авторы этой гипотезы Мак-Каллок и Питс особо подчеркивали, что сканирование позволяет объяснить один важный феномен. Дело в том, что информация от первичной зрительной коры проецируется далее по волокнам белого вещества через пучки аксонов, явно недостаточные по своему объему для одновременной передачи всего состояния этой зоны коры. А значит, делали вывод они, сканирование позволяет использовать не только пространственный, но и временной код, что обеспечивает последовательную передачу требуемой информации.

Такая проблема узости проецирующих пучков существует не только для первичной зрительной коры, но и для всех остальных зон мозга. Количество волокон в проекционных путях много меньше количества нейронов, формирующих пространственную картину активности. Связи между зонами явно не в состоянии параллельно передать весь пространственно распределенный сигнал, а значит, требуется понимание того, как происходит сжатие и распаковка транслируемой по ним информации. Предположение о сканировании, хотя и не дает ответа на вопрос о самом механизме кодирования, тем не менее позволяет поставить перед собой правильные вопросы.

Наша модель в объяснении ритмов мозга опирается на приведенное выше описание природы метаботропной активности. Использование представления о том, что в процесс создания ритмов вовлечены не только синапсы нейронов, но и метаботропные рецептивные кластеры, позволяет получить результат, качественно отличающийся от всех классических теорий. Но перед тем как перейти к описанию этого, хочу сделать предупреждение. Я сознательно буду описывать упрощенные идеализированные модели, ставя им в соответствие определенные процессы, свойственные реальному мозгу, но, не утверждая, что мозг работает именно так. Наша задача – показать базовые принципы, понимая, что эволюция ушла далеко вперед и их подлинная реализация значительно хитрее. Можно провести аналогию с развитием вычислительной техники. Современный компьютер достаточно сложен, и если мы начнем описывать базовые принципы классических вычислительных устройств, то окажется, что в чистом виде их уже практически невозможно встретить в современных системах. Об этом говорит сайт https://intellect.icu . Базовое представление – процессор считывает из памяти программу и данные, выполняет над данными действия, предписанные программой, и записывает результаты обратно в память. А теперь добавьте к этому использование кэша различных уровней, многопоточность, гиперпоточность, параллельные вычисления с использованием локальной, групповой и общей памяти и тому подобное. И окажется, что трудно найти в реальном компьютере буквальное соблюдение простых правил. Собственно, все это надо учитывать, сопоставляя последующее описание с работой реального мозга.

Итак, возьмем модель участка коры, на которой создадим компактный паттерн вызванной активности. Пока оставим вопрос, как возник этот паттерн. Просто будем полагать, что есть элементы, на которых присутствует постоянный импульсный сигнал. На рисунке ниже нейроны, образующие такой паттерн, помечены красным. В реальной коре это соответствует аксонам, передающим пачечную активность, то есть выдающим серию спайков с высокой частотой. Эти аксоны могут принадлежать нейронам этой же зоны коры, находящимся в состоянии вызванного возбуждения, либо они могут быть проекционными волокнами, идущими от других участков мозга.


Паттерн вызванной активности

Теперь заставим свободные нейроны генерировать редкие случайные импульсы. При этом наложим условие, что для случайного спайка требуется определенный уровень окружающей активности. Это значит, что случайные спайки смогут возникнуть только поблизости от уже активных нейронов. В нашем случае они появятся в окрестности паттерна вызванной активности. На рисунке ниже случайные спайки показаны зеленым цветом.

Обычно всю активность нейронов, которая не является вызванной, называют спонтанной или фоновой. Это не очень удачно, так как настраивает на восприятие всей этой активности как случайной. Далее мы покажем, что, в основном, фоновая активность строго предопределена и нисколько не случайна. И только малая ее часть – это действительно совершенно случайные спайки. Такие случайные спайки мы сейчас и создали вокруг активного паттерна.


Первый шаг моделирования. Спонтанная активность на фоне вызванной активности

Смоделируем на наших формальных нейронах метаботропные рецептивные кластеры. Для этого дадим нейронам возможность запоминать, когда это необходимо, картину активности ближайшего окружения. Причем не ограничимся одной картиной для одного нейрона, как это было бы, запоминай мы на синапсах, а позволим каждому нейрону хранить множество таких картин.

Сделаем так, что наличие собственного случайного спайка и высокой окружающей активности будет каждый раз основанием запоминать картину окружающих импульсов (рисунок ниже). Далее наши нейроны будут давать единичные спайки каждый раз, когда будет повторяться одна из этих запомненных локальных картин. Чтобы не путать их со случайными спайками, будем называть эти спайки волновыми.


Область фиксации активности для одного из нейронов, выдавших спонтанный спайк (он в центре квадрата). При моделировании для простоты использовались квадратные рецептивные поля, что хотя и не соответствует полям слежения у реальных нейронов, качественно не влияет на результат

В итоге на следующем шаге моделирования (рисунок ниже) мы получим картину, в которой будут те же, что и ранее, нейроны с вызванной активностью (красные), нейроны, среагировавшие на запомненные на предыдущем шаге локальные образы (белые), и нейроны, сгенерировавшие спонтанный спайк (зеленые).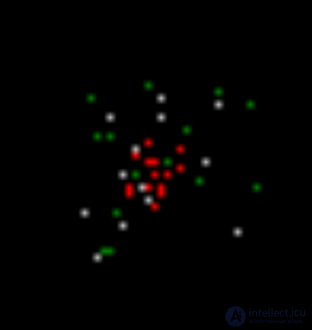


Второй шаг моделирования. Красные – вызванная активность, белые – волновая активность, зеленые – спонтанная активность

Повторяя шаги моделирования, мы получим распространяющуюся по коре активность с определенным уникальным случайно созданным узором.
Теперь введем условие усталости нейронов. Сделаем так, что после нескольких метаботропных (волновых) спайков нейроны будут терять на время, необходимое для релаксации, способность генерировать новые импульсы. Это приведет к тому, что активность будет распространяться не сплошной областью, а пульсирующими волнами, разбегающимися от своего источника.

Чтобы предотвратить «засорение», заблокируем спонтанную активность в областях, где велико количество релаксирующих нейронов. В результате мы получим кольцо нейронов с волновой активностью, разбегающееся от паттерна вызванной активности (рисунок ниже).


Распространение фронта волны. Синие – нейроны, пребывающие в состоянии релаксации

Получившаяся волна по мере удаления от своего центра будет терять плотность фронта и рано или поздно затухнет. На рисунке ниже можно проследить первый цикл ее жизни.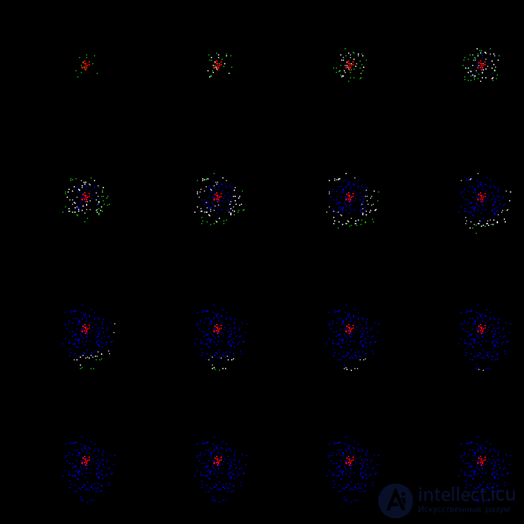


Первый цикл распространения волны идентификатора

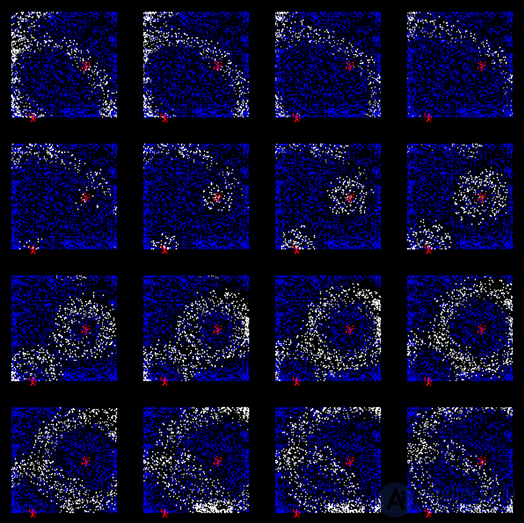
После того как период релаксации пройдет, запустится новая волна. Теперь она будет подхвачена нейронами, уже прошедшими обучение, и распространится несколько дальше. С каждым новым циклом волна будет расширять границы своего распространения, пока не достигнет краев зоны. Чтобы предотвратить неограниченный рост плотности фронта волны, введем еще одно ограничение: запретим спонтанную активность для нейронов, когда общая активность вокруг них превышает определенный порог.

Через какое-то время мы получим кору, обученную распространять уникальную по своему узору волну активности, соответствующую заданному изначально паттерну вызванной активности (рисунок ниже).


Распространение волны по уже обученной коре (после 200 тактов обучения)

Ниже видео процесса волнового обучения:



Обратите внимание: когда кора уже обучена на распространение волны от определенного паттерна, спонтанные (случайные) спайки исчезают. Такая «опытная» волна формируется за счет волновых, неслучайных спайков. Случайные спайки появляются только при обучении, когда фронт волны доходит до еще необученных или слабо обученных территорий. В этот момент спонтанные импульсы создают случайное продолжение волнового узора, которое тут же запоминается на поверхности нейронов, участвующих в этой волне. Но как только обучение заканчивается, волна от знакомого коре паттерна начинает распространяться по уже созданному волновому шаблону, каждый такт в точности повторяя на своем пути один и тот же уже неслучайный узор.

Обучение коры не обязательно должно быть поэтапным. При моделировании подбором параметров можно добиться, чтобы зародившаяся волна была самодостаточной. То есть, чтобы она не затухала на первых тактах, а сразу распространялась на все пространство (рисунок ниже).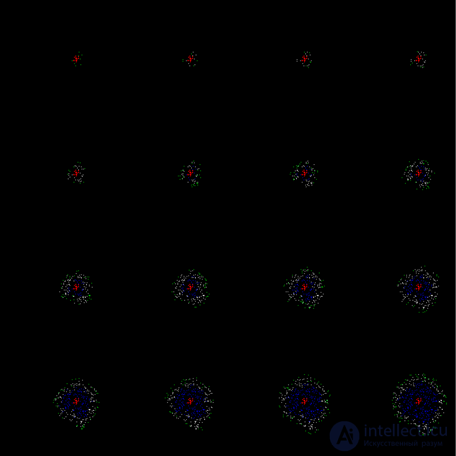


Пример незатухающего на первом цикле распространения обучающей волны

Так как ширина фронта волны постоянна, то его площадь возрастает по мере удаления от источника. Это соответствует тому, что в распространении активности участвует все больше нейронов. Если проследить суммарный потенциал, создаваемый ими, то получатся графики, напоминающие то, что мы видим на энцифолограммах (рисунок ниже).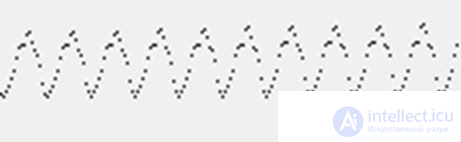


График ритмической активности модели с одним источником

Обратите внимание, что появление ритмов, наблюдаемых на таких «энцефалограммах», – это не ритм «дыхания» коры. То есть не синхронизация совместных всплесков активности, как полагается в большинстве существующих моделей, а изменение количества нейронов, вовлеченных в распространение расходящихся волн. Если новые волны будут излучаться еще до того, как исчезнут фронты предыдущих волн, то их сложение даст более сглаженную картину. При определенном подборе параметров на модели воспроизводятся ситуации, когда распространение волн практически не сопровождается суммарной ритмической активностью. Это можно соотнести с тем фактом, что у порядка 10 процентов людей на электроэнцефалограммах волновая активность не прослеживается.

Если теперь взять новый паттерн вызванной активности, то кора создаст волны, распространяющиеся и от него. Более того, такая кора обучается создавать волны для любого устойчивого паттерна вызванной активности. За счет того, что один и тот же нейрон может хранить множество локальных образов, он может быть частью сразу множества различных волн, соответствующих разным паттернам. Если мы захотим большей уникальности волн, то достаточно по мере накопления у нейрона запомненных им локальных образов снижать вероятность его спонтанного спайка.

Для запомненных локальных образов имеет смысл ввести механизм консолидации. То есть не фиксировать образ сразу на века, а установить время, в течение которого образ должен определенное количество раз повториться. Так как обучение волновому распространению и формирование устойчивых паттернов вызванной активности – процессы параллельные, то консолидация может позволить стереть следы неудачного обучения.

Но самое главное во всем этом – это уникальность каждой из полученных волновых историй. В любом месте, через которое проходит волна, она создает единственный, характерный только для нее рисунок. Это значит, что если на поверхности коры есть паттерн вызванной активности, который кодирует какое-либо событие, то волна, вызванная им, распространит информацию об этом по всему пространству коры. В каждом конкретном месте эта волна создаст свой неповторимый узор, уникальный только для этого события. Любое другое событие создаст в этом месте иной узор, связанный со своей волной. Это значит, что находясь в любом месте, мы можем настроиться на «прием» волны от какого-либо конкретного события и зафиксировать, когда оно произойдет по приходу волны с соответствующим узором.

В нашей модели получается, что фундаментальные свойства коры – это:

• способность генерировать волны, расходящиеся от паттернов вызванной активности;
• способность обучаться, проводить уникальные и стабильные для каждого паттерна узоры волн;
• будучи обученной, способность распространять волны активности, возникающие вокруг устойчивых паттернов вызванной активности.

Каждому уникальному паттерну вызванной активности соответствует уникальная по своему узору волна, которую можно назвать идентификатором этого паттерна.

Теперь процесс обучения можно грубо представить следующим образом:

• статистически устойчивые сигналы ведут к формированию нейронов-детекторов, которые за счет синаптической пластичности обучаются реагировать на определенные закономерности;
• нейроны-детекторы, относящиеся к одной закономерности, образуют устойчивый паттерн;
• каждый устойчивый паттерн по мере своей активности обучает кору распространять уникальную волну, соответствующую только этому паттерну, что можно трактовать как идентификатор этого паттерна;
• каждое место коры, куда распространяются соответствующие волны, получает возможность узнать, какова общая информационная картина на текущий момент.

Из сказанного выше следует, что для своей полноценной работы мозг должен не только сформировать нейроны-детекторы различных явлений, но и обучить кору распространять соответствующие информационные волны. Это хорошо согласуется с тем фактом, что ритмическая активность у детей слабо выражена сразу после рождения и увеличивается по мере взросления.

Когда мы говорим о структурах мозга, которые реагируют на определенные явления, то в нашей концепции возникает их очевидный дуализм. Эти структуры не описываются исключительно какими-либо нейронами или группами нейронов, они дополняются еще и идентификационными волнами, которые позволяют распространить соответствующую информацию. Но, что интересно, – в каждом конкретном месте, через которое проходит волна, она ведет себя так же, как и породивший ее паттерн. В моментальном временном срезе она сама является паттерном, порождающим продолжение волны.

Нетрудно заметить, что такое распространение идентификационных волн повторяет принцип Гюйгенса-Френеля, описывающий распространение волн света. Суть его в том, что каждую точку фронта световой волны можно рассматривать как центр вторичного возмущения. Каждый такой центр порождает вторичные сферические волны. Итоговое световое поле есть интерференция этих волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени, и так далее.


Рефракция (слева) и интерференция (справа) по Гюйгенсу-Френелю (Nordmann)

Разница в природе паттерна вызванной активности и паттерна, возникающего в процессе распространения волны, может быть обнаружена только по анализу причины активности входящих в них нейронов. Для вызванной активности – это картина на синапсах, для паттерна распространения – реакция метаботропных рецепторов. То есть отражение мозгом каких-либо явлений – это одновременно и паттерн и волна, причем в каждый конкретный момент времени, когда мы попытаемся зафиксировать распространение этой волны, мы увидим паттерн, отличный по узору, но не по сути от того, что дал начало волне.

Нетрудно заметить, что описанный дуализм достаточно точно соответствует дуализму элементарных частиц. Как известно, каждая частица – это одновременно и частица и волна. В зависимости от того, какие обстоятельства мы рассматриваем, частица может проявлять как волновые, так и корпускулярные свойства. Современная физика констатирует этот факт, но не дает ему объяснения. То, что мы описали о дуализме информационных образов, к счастью, несколько нагляднее, чем дуализм элементарных частиц. Конечно, напрашивается вопрос, можно ли продлить эти аналогии и использовать их для понимания физической картины мира? Это очень серьезный вопрос, и позже мы поговорим о случайности или не случайности такого совпадения.

Из дуализма информационных образов проистекают важные следствия. Как и частицы с разными спинами, два паттерна от разных волн могут находиться в одной пространственной области, не мешая друг другу. Более того, каждый из них вызывает продолжение собственной волны, не внося взаимных искажений. Если мы создадим несколько паттернов и обучим кору на распространение волн от каждого из них, то активировав эти паттерны совместно, мы сможем наблюдать прохождение волн друг сквозь друга с сохранением собственной уникальности (рисунок ниже).


Моделирование прохождения волн от двух источников

Это сильно отличается от сплошных волновых процессов. Например, при распространении волн в воде или воздухе, в колебаниях принимают участие сразу все молекулы. Столкновение двух волн затрагивает весь контактирующий объем, что ведет к интерференции. Поведение каждой молекулы определяется действием сразу обеих волн. В результате мы получаем интерференционную картину, которая уже не столь проста, как каждая из волновых картин в отдельности. В нашем же случае каждая из волн распространяется, затрагивая только малую часть всех доступных нейронов. При пересечении двух информационных волн общих для них нейронов, способных создать интерференцию, оказывается слишком мало, чтобы повлиять на распространение каждой из них. В результате, волны сохраняют свою информационную картину, неискаженной от встречи с другой волной.

Определенная изящность описываемой системы еще и в том, что нейроны могут выполнять одновременно две функции. Каждый нейрон может быть детектором, настраиваясь за счет изменения синаптических весов на определенный образ. При этом этот же нейрон за счет информации, записанной на его метаботропных кластерах, может принимать участие в распространении различных информационных волн.

Стоит почувствовать разницу между свойствами нейрона как детектора и как участника распространения волновой активности. Казалось бы, и там и там он реагирует на определенную картину активности своего окружения. В действительности это два принципиально разных свойства. Относительно плавная настройка синаптических весов позволяет нейрону обучаться на выделение скрытых факторов. Моментальная фиксация образов внесинаптическими кластерами обеспечивает запоминание того, что есть прямо сейчас. Синапсы воспринимают масштабную картину со всего рецептивного поля нейрона. Метаботропным рецептивным кластерам доступна урезанная картина активности, ограниченная синапсами, образующими их синаптические ловушки. Набор синаптических весов у обычного нейрона только один, а вот идентификационных образов он может хранить десятки и сотни тысяч. Синаптическое узнавание порождает вызванную активность, то есть длительный пакет импульсов. Несколько нейронов-детекторов за счет этого создают паттерн вызванной активности. Метаботропное узнавание дает единичный спайк. Совокупность таких спайков создает фронт идентификационной волны.

При моделировании наблюдается, что дальность распространения идентификатора зависит от того, насколько активно проявляет себя создающий волну паттерн. Применяя механизм консолидации, то есть, вводя критерии забывания, срабатывающего, если активность не повторяется должным образом, удается получить эффект, когда часто повторяющие паттерны обучают всю кору на распространение своих волн, а редкие сочетания создают области локального распространения. Причем размеры этих областей не фиксированы, а охотно растут, если соответствующее явление начинает проявлять себя чаще. В таком поведении можно найти определенный резон. Возможно, что и реальная кора ведет себя похожим образом.

Когда мне удалось сформулировать описанные выше волновые принципы, моделирование в рамках нашего проекта перешло на новый качественный уровень. Было ощущение, что вместо каменного топора мы внезапно получили отбойный молоток. В следующих частях я покажу как использование волновой нейросетевой модели позволяет объяснить многие казавшиеся ранее загадочными свойства мозга.

Если я не полностью рассказал про волны мозга? Напиши в комментариях Надеюсь, что теперь ты понял что такое волны мозга и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика мышления

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.