Лекция
Привет, Вы узнаете о том , что такое прогнозирование с помощью нейронных сетей, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое прогнозирование с помощью нейронных сетей , настоятельно рекомендую прочитать все из категории Практическое применение методов искусственного интеллекта.
Нейронные сети - это очень мощный и гибкий механизм прогнозирования. При определении того, что нужно прогнозировать, необходимо указывать переменные, которые анализируются и предсказываются. Здесь очень важен требуемый уровень детализации. На используемый уровень детализации влияет множество факторов:
доступность и точность данных, стоимость анализа и предпочтения пользователей результатов прогнозирования. В ситуациях, когда наилучший набор переменных неясен, можно попробовать разные альтернативы и выбрать один из вариантов, дающий наилучшие результаты. Обычно так осуществляется выбор при разработке прогнозирующих систем, основанных на анализе исторических данных.
Второй важный этап при построении нейросетевой прогнозирующей системы - это определение следующих трех параметров: периода прогнозирования, горизонта прогнозирования и интервала прогнозирования.
Общая постановка проблемы. Способности нейронной сети к прогнозированию напрямую следуют из ее способности к обобщению и выделению скрытых зависимостей между входными и выходными данными. После обучения сеть способна предсказать будущее значение некой последовательности на основе нескольких предыдущих значений и/или каких-то существующих в настоящий момент факторов.
Постановка задачи исследования. Необходимо подготовить данные для обучения и проверки корректности работы нейронной сети, выбрать топологию нейронной сети, подобрать ее характеристики и параметры обучения.
Период прогнозирования - это основная единица времени, на которую делается прогноз. Горизонт прогнозирования - это число периодов в будущем, которые покрывает прогноз. То есть, может понадобиться прогноз на 10 дней вперед, с данными на каждый день. В этом случае период - сутки, а горизонт - 10 суток. Наконец, интервал прогнозирования - частота, с которой делается новый прогноз. Часто интервал прогнозирования совпадает с периодом прогнозирования. Выбор периода и горизонта прогнозирования обычно диктуется условиями принятия решений в области, для которой производится прогноз. Выбор этих двух параметров - едва не самое трудное в нейросетевом прогнозировании. Для того чтобы прогнозирование имело смысл, горизонт прогнозирования должен быть не меньше, чем время, необходимое для реализации решения, принятого на основе прогноза. Таким образом, прогнозирование очень сильно зависит от природы принимаемого решения. В некоторых случаях, время, требуемое на реализацию решения, не определено, например, как в случае поставки запасных частей для пополнения запасов ремонтных предприятий. Существуют методы работы в условиях подобной неопределенности, но они повышают вариацию ошибки прогнозирования. Поскольку с увеличением горизонта прогнозирования точность прогноза, обычно, снижается, часто можно улучшить процесс принятия решения, уменьшив время, необходимое на реализацию решения и, следовательно, уменьшив горизонт и ошибку прогнозирования.
В некоторых случаях не так важно предсказание конкретных значений прогнозируемой переменной, как предсказание значительных изменений в ее поведении. Такая задача возникает, например, при предсказании момента, когда текущее направление движения рынка (тренд) изменит свое направление на противоположное.
Точность прогноза, требуемая для конкретной проблемы, оказывает огромное влияние на прогнозирующую систему. Также огромное влияние на прогноз оказывает обучающая выборка.
Первое, с чем сталкивается пользователь любого нейропакета - это необходимость подготовки данных для нейросети. На практике именно предобработка данных может стать наиболее трудоемким элементом нейросетевого анализа. Причем, знание основных принципов и приемов предобработки данных не менее, а может быть даже более важно, чем знание собственно нейросетевых алгоритмов. Последние, как правило, уже "зашиты" в различных нейроэмуляторах, доступных на рынке. Сам же процесс решения прикладных задач, в том числе и подготовка данных, целиком ложится на плечи пользователя.
Рассмотрим задачу прогнозирования объема продаж товаров предприятия. Среда является недетерминированной, так как обычные методы не позволяют со сто процентной уверенностью сказать, что будет в следующий момент времени и выявить все факторы, которые влияют на прогнозируемую величину практически невозможно (можно только ограничить набор факторов). Имеется следующий набор финансовых индикаторов:
Деятельность предприятия:
Внешние факторы:
В результате комплексных исследований были выявлены вторичные факторы, оказывающие влияние на объем продаж предприятия, которые необходимо учитывать. Эти показатели представлены в таблице 1 (взята из диссертации Бычкова А.). Как видно из таблицы, перечисленные параметры имеют различную значимость, значения этих параметров имеют разную природу и добываются из различных источников. В результате содержательного анализа перечисленных параметров выявлено, что некоторые из них невозможно включить в модель из-за невозможности получения данных, а отдельные не оказывают сильного влияния на динамику модели и, поэтому их можно без существенной потери точности исключить из модели.
Таблица 1
Вторичные параметры используемые для принятия решений
|
Независимые переменные |
Значимость |
|
1.Концентрация |
++++ |
|
2. Состояние склада |
++++ |
|
3. Экономия от масштаба |
++ |
|
4. Дифференциация продукта |
+++ |
|
5. Интенсивность рекламы |
+++ |
|
6. Отношение активы - объем производства |
++ |
|
7. Рост. |
+++ |
|
8. Диверсификация |
++ |
|
9. Географическое размещение. |
+ |
|
10. Об этом говорит сайт https://intellect.icu . Риск |
++++ |
|
11. Экспорт |
+ |
|
12. Импорт |
+ |
|
13. Рыночная доля |
+++ |
|
14. Концентрация покупателей |
+ |
|
15. Интенсивность исследований и разработок |
+ |
|
16. Стратегические группировки |
+ |
Следует отметить, что сама история продаж предприятия дает для обучения нейросети примерно 60 % необходимой информации (на основании опыта автора).
Задача прогнозирования объема продаж предприятия обладает теми особенностями, которые делают целесообразным использование нейросетевых методов моделирования и, в частности, топологии «внутренний учитель»:
а) таблица данных может иметь небольшой размер ;
б) в таблице данных могут присутствовать пропуски данных;
в) в данных возможны искажения («шум»);
г) необходима возможность адаптации модели при поступлении новых данных;
д) трудно получить линейную алгебраическую модель;
е) большое количество позиций номенклатуры.
Общий алгоритм прогнозирования с помощью нейронной сети
Алгоритм состоит из следующих пунктов:
Поясним термин «таблицы окон». Данные необходимо преобразовать по специальной схеме. Сначала преобразуем полученный временный ряд в ряд приращений прогнозируемой величины, т. е. будем прогнозировать изменение величины, а не абсолютные значения ряда. Затем выберем глубину погружения, т.е. количество временных интервалов, по которым мы будем прогнозировать следующий. Возьмем глубину погружения равной 4, т.е. прогнозирование величины на следующую итерацию будет осуществляться по результатам четырех предыдущих итераций. Далее следует преобразовать величину к следующему виду:
Таблица 4.1
Первый вариант «окна» данных
|
Hist1 |
Hist2 |
Hist3 |
Hist4 |
Hist0 |
|
D-1 |
D-2 |
D-3 |
D-4 |
D |
|
D-2 |
D-3 |
D-4 |
D-5 |
D-1 |
|
D-3 |
D-4 |
D-5 |
D-6 |
D-2 |
|
… |
… |
… |
… |
… |
Первые четыре колонки являются входами нейросети, последняя – выход, т. е. на основе предыдущих значений изменения величины прогнозируется следующее значение ряда. Таким образом, мы получаем так называемое «скользящее окно», в котором представлены данные за пять недель. Окно можно двигать по временной оси и изменять его ширину. Чтобы учесть предыдущие годы и учесть возможные сезонные зависимости добавим еще один столбец в выборку, который показывает изменение величины в прошлый год за тот же период.
Таблица 4.2
Второй вариант «окна» данных
|
LastY |
Hist1 |
Hist2 |
Hist3 |
Hist4 |
Hist0 |
|
L |
D-1 |
D-2 |
D-3 |
D-4 |
D |
|
L-1 |
D-2 |
D-3 |
D-4 |
D-5 |
D-1 |
|
L-2 |
D-3 |
D-4 |
D-5 |
D-6 |
D-2 |
|
… |
… |
… |
… |
… |
… |
Таким образом, готовится обучающая выборка и именно в таком виде предоставляются данные для последующего анализа. Можно не ограничиваться только прошлым годом, а подавать данные за несколько предыдущих лет, но следует учитывать, что сеть в таком случае разрастается, что иногда приводит к плохим результатам.
К недостаткам прогнозирования с помощью нейронных сетей можно отнести следующее: длительное время обучения, проблема переобучения, трудность определения положения обучающей выборки и значащих входов.
Например, данные по продажам нового товара.
Схему решения задачи прогнозирования можно представить в виде последовательности этапов (рис. 1).
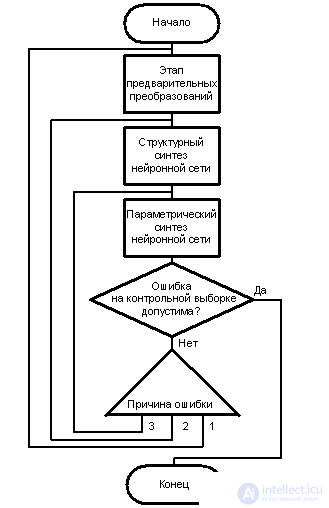
Рис. 1 Схема решения задач прогнозирования
Этап предварительных преобразований. Если временной ряд порождается динамической системой, т.е. значения {a(t)} – произвольная функция состояния такой системы, существует такое число d, что d предыдущих значений временного ряда однозначно определяет следующее значение. На практике большинство прогнозируемых временных рядов порождаются сложными динамическими системами, для которых велико значение d. Кроме того, в самом временном ряде может присутствовать случайная составляющая. Поэтому на данном этапе выполняются предварительные преобразования исходных данных позволяющие уменьшить ошибку прогнозирования.
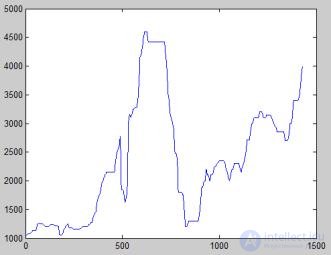
Рис. 2 Динамика цен на подсолнечник с 2007 по 2010гг
На этапе обучения нейронная сеть восстанавливает целевую функцию по множеству наборов обучающей выборки, т.е. решает задачу интерполяции. На этапе использования обученной нейронной сети (получении прогноза) она будет использовать восстановленную зависимость для получения прогнозируемой величины, т.е. решать задачу экстраполяции. Для корректного решения задачи экстраполяции как задачи интерполяции необходимо обеспечить стационарность временного ряда признаков, распределение значений ряда должно быть инвариантно относительно момента времени, для которого оно построено. Для этого продифференцируем временной ряд: x’i=xi+1-xi (рис. 3).
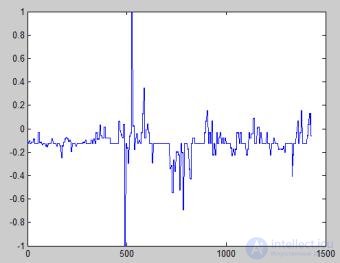
Рис. 3 Продифференцированный временной ряд
Для улучшения качества и скорости обучения нейронной сети необходимо преобразовать входные данные к диапазону [-1,1]. Формула пересчета значения признака x для i-го примера выборки в интервал [a,b] такова:
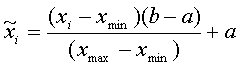 , (1)
, (1)
где xmin , xmax - минимальное и максимальное выборочные значения признака.
Из данного множества выделяются два непересекающихся подмножества, хронологически следующих одно за другим. Одно из них представляет собой обучающую выборку, на которой будет выполняться обучение нейронной сети. Другое подмножество представляет собой контрольную выборку, которая не предъявляется нейронной сети в процессе обучения и используется для проверки качества прогноза. Обучающая и контрольная выборки относятся как 2:1.
Этап структурного синтеза нейронной сети. На данном этапе производится выбор архитектуры сети и структура связей между нейронами. В результате исследований в качестве топологии нейронной сети выбран персептрон с 30 входами (x), 80 нейронами скрытого слоя (s) и одним выходным (y).
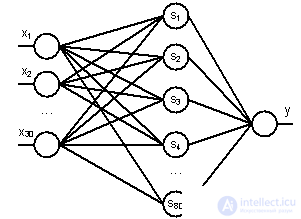
Рис. 4 Схема нейронной сети
Персептрон представляет собой сеть, состоящую из нескольких последовательно соединенных слоев формальных нейронов МакКаллока и Питтса. На низшем уровне иерархии находится входной слой, состоящий из сенсорных элементов, задачей которого является только прием и распространение по сети входной информации. Далее имеются один или, реже, несколько скрытых слоев. Каждый нейрон на скрытом слое имеет несколько входов, соединенных с выходами нейронов предыдущего слоя или непосредственно со входными сенсорами X1..Xn, и один выход. Нейрон характеризуется уникальным вектором весовых коэффициентов w. Веса всех нейронов слоя формируют матрицу, которую мы будем обозначать W. Функция нейрона состоит в вычислении взвешенной суммы его входов с дальнейшим нелинейным преобразованием ее в выходной сигнал.
Выходы нейронов последнего, выходного, слоя описывают результат классификации Y=Y(X). Особенности работы персептрона состоят в следующем. Каждый нейрон суммирует поступающие к нему сигналы от нейронов предыдущего уровня иерархии с весами, определяемыми состояниями синапсов, и формирует ответный сигнал (переходит в возбужденное состояние), если полученная сумма выше порогового значения. Персептрон переводит входной образ, определяющий степени возбуждения нейронов самого нижнего уровня иерахии, в выходной образ, определяемый нейронами самого верхнего уровня. Число последних, обычно, сравнительно невелико. Состояние возбуждения нейрона на верхнем уровне говорит о принадлежности входного образа к той или иной категории.
Традиционно рассматривается аналоговая логика, при которой допустимые состояния синаптических связей определяются произвольными действительными числами, а степени активности нейронов - действительными числами между 0 и 1. Иногда исследуются также модели с дискретной арифметикой, в которой синапс характеризуется двумя булевыми переменными: активностью (0 или 1) и полярностью (-1 или +1), что соответствует трехзначной логике. Состояния нейронов могут при этом описываться одной булевой переменной. Данный дискретный подход делает конфигурационное пространство состояний нейронной сети конечным (не говоря уже о преимуществах при аппаратной реализации).
Параметрический синтез нейронной сети. В качестве метода обучения нейронной сети будет использоваться алгоритм обратного распространения ошибки. Основная идея обратного распространения состоит в том, как получить оценку ошибки для нейронов скрытых слоев. Заметим, что известные ошибки, делаемые нейронами выходного слоя, возникают вследствие неизвестных пока ошибок нейронов скрытых слоев. Чем больше значение синаптической связи между нейроном скрытого слоя и выходным нейроном, тем сильнее ошибка первого влияет на ошибку второго. Следовательно, оценку ошибки элементов скрытых слоев можно получить, как взвешенную сумму ошибок последующих слоев. При обучении информация распространяется от низших слоев иерархии к высшим, а оценки ошибок, делаемые сетью - в обратном направлении.
На этапе обучения происходит вычисление синаптических коэффициентов w. При этом в отличие от классических методов в основе лежат не аналитические вычисления, а методы обучения по образцам с помощью примеров сгруппированных в обучаемом множестве. Для каждого образа из обучающей выборки считается известным требуемое значение выхода нейронной сети. Этот процесс можно рассматривать как решение оптимизационной задачи. Ее целью является минимизации функции ошибки или невязки Е на обучающем множестве путем выбора значений синоптических коэффициентов w.
В качестве активационной функции нейронов скрытого слоя необходимо взять сигмоидальную функцию, т.к. для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. (2).
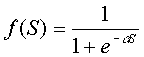 . (2)
. (2)
Сигмоид ограничивает диапазон изменения выходного сигнала между нулем и единицей, что повышает устойчивость нейросети. Благодаря нелинейности функции активации нейроны обладают хорошей обучаемостью.
Активационной функцией нейрона выходного слоя выбрана линейная функция (3).
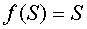 (3)
(3)
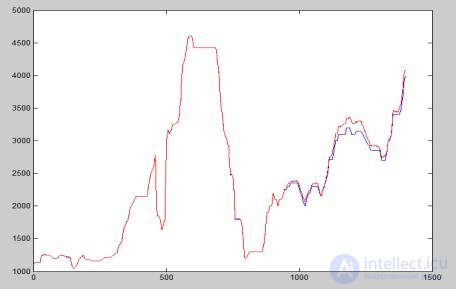
Рис. 5 Проверка обученной нейронной сети
Проверка ошибки прогноза на контрольной выборке. Если значение ошибки находится в допустимых пределах, то задача считается решенной, и обученная нейронная сеть используется для получения прогноза. В данном случае ошибка не превышает 4%.
Опираясь на результаты полученных экспериментальным путем ведущими разработчиками в области нейронных сетей, данная топология нейронной сети и метод ее обучения является одним из оптимальных в задачах прогнозирования.
Выводы.
Нейронные сети - исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости. В статье была доказана возможность и эффективность применения нейронных сетей для прогнозирования временных рядов, рассмотрены топология искусственной нейронной сети, метод ее обучения, входные данные и их предобработка и другие характеристики нейронной сети для прогнозирования финансово-хозяйственных показателей сельскохозяйственного предприятия, выделены основные задачи, которые необходимо выполнить для ее разработки.
Комментарии
Оставить комментарий
Практическое применение методов искусственного интеллекта
Термины: Практическое применение методов искусственного интеллекта