Лекция
Сразу хочу сказать, что здесь никакой воды про многоагентная система, и только нужная информация. Для того чтобы лучше понимать что такое многоагентная система, многоагентные системы, мультиагентные системы , настоятельно рекомендую прочитать все из категории Интеллектуальные агенты . Многоагентные системы.
многоагентная система (МАС, англ. Multi-agent system) — это система, образованная несколькими взаимодействующимиинтеллектуальными агентами. многоагентные системы могут быть использованы для решения таких проблем, которые сложно или невозможно решить с помощью одного агента или монолитной системы (англ.). Примерами таких задач являются онлайн-торговля , ликвидация чрезвычайных ситуаций , и моделирование социальных структур .
мультиагентные системы — это активно развивающееся направление искусственного интеллекта, которое в настоящее время еще находится в стадии становления.
В классической теории искусственного интеллекта решение какой-либо задачи сводится к созданию некоторой одной интеллектуальной системы, называемой агентом, которая, имея в своем распоряжении все необходимые знания, способности и вычислительные ресурсы, способна решить некоторую глобальную проблему.
Многоагентные системы или мультиагентные системы – это направление искусственного интеллекта, которое для решения сложной задачи или проблемы использует системы, состоящие из множества взаимодействующих агентов.
В теории многоагентных систем (также часто встречается название «мультиагентные системы») за основу берется противоположный принцип. Считается, что один агент владеет всего лишь частичным представлением о глобальной проблеме, а значит, он может решить лишь некоторую часть общей задачи. В связи с этим для решения сложной задачи необходимо создать некоторое множество агентов и организовать между ними эффективное взаимодействие, что позволит построить единую многоагентную систему. В многоагентных системах весь спектр задач по определенным правилам распределяется между всеми агентами, каждый из которых считается членом организации или группы. Распределение заданий означает присвоение каждому агенту некоторой роли, сложность которой определяется исходя из возможностей агента.
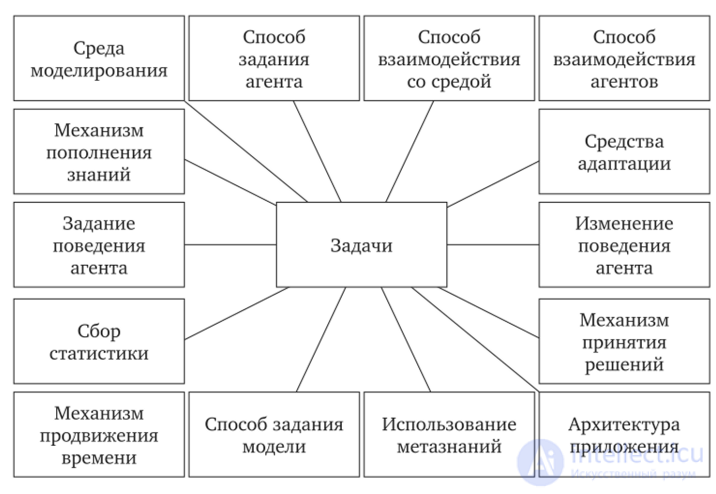
Рис. 6.4. Задачи, решаемые при создании MAC
Рис. 6.5. Методы и технологии возможных решений создания агентных моделей
В многоагентной системе агенты имеют несколько важных характеристик :
Обычно в многоагентных системах исследуются программные агенты. Тем не менее, составляющими мультиагентной системы могут также быть роботы, люди или команды людей. Также, многоагентные системы могут содержать и смешанные команды.
В многоагентных системах может проявляться самоорганизация и сложное поведение даже если стратегия поведения каждого агента достаточно проста. Это лежит в основе так называемого роевого интеллекта.
Агенты могут обмениваться полученными знаниями, используя некоторый специальный язык и подчиняясь установленным правилам «общения» (протоколам) в системе. Примерами таких языков являются Knowledge Query Manipulation Language (KQML) и FIPA’s Agent Communication Language (ACL).
Обычный агент
В многоагентной системе агенты имеют несколько важных характеристик :
Обычно в многоагентных системах исследуются программные агенты . Об этом говорит сайт https://intellect.icu . Тем не менее, составляющими мультиагентной системы могут также быть роботы , люди или команды людей. Также, многоагентные системы могут содержать и смешанные команды.
В многоагентных системах может проявляться самоорганизация и сложное поведение даже если стратегия поведения каждого агента достаточно проста. Это лежит в основе так называемого роевого интеллекта.
Агенты могут обмениваться полученными знаниями, используя некоторый специальный язык и подчиняясь установленным правилам «общения» (протоколам) в системе. Примерами таких языков являются Knowledge Query Manipulation Language (KQML) и FIPA’s Agent Communication Language (ACL).
Изучение многоагентных систем связано с решением проблем искусственного интеллекта.
Темы для исследования в рамках МАС:
Многие МАС имеют компьютерные реализации, основанные на пошаговом имитационном моделировании. Компоненты МАС обычно взаимодействуют через весовую матрицу запросов,
Speed-VERY_IMPORTANT: min=45 mph, Path length-MEDIUM_IMPORTANCE: max=60 expectedMax=40, Max-Weight-UNIMPORTANT Contract Priority-REGULAR
и матрицу ответов,
Speed-min:50 but only if weather sunny, Path length:25 for sunny / 46 for rainy Contract Priority-REGULAR note - ambulance will override this priority and you'll have to wait
Модель «Запрос — Ответ — Соглашение» — обычное явление для МАС. Схема реализуется за несколько шагов:
Для последнего шага обычно требуется еще несколько (более мелких) актов обмена информацией. При этом принимаются во внимание другие компоненты, в том числе уже достигнутые «соглашения» и ограничения среды.
Другой часто используемой парадигмой в МАС является «феромон», где компоненты «оставляют» информацию для следующих в очереди или ближайших компонентов. Такие «феромоны» могут испаряться со временем, то есть их значения могут изменяться со временем.
МАС также относятся к самоорганизующимся системам, так как в них ищется оптимальное решение задачи без внешнего вмешательства. Под оптимальным решением понимается решение, на которое потрачено наименьшее количество энергии в условиях ограниченных ресурсов.
Главное достоинство МАС — это гибкость. Многоагентная система может быть дополнена и модифицирована без переписывания значительной части программы. Также эти системы обладают способностью к самовосстановлению и обладают устойчивостью к сбоям, благодаря достаточному запасу компонентов и самоорганизации.
Многоагентные системы применяются в нашей жизни в графических приложениях, например, в компьютерных играх. Агентные системы также были использованы в фильмах . Теория МАС используется в составных системах обороны. Также МАС применяются в транспорте, логистике, графике, геоинформационных системах и многих других. Многоагентные системы хорошо зарекомендовали себя в сфере сетевых и мобильных технологий, для обеспечения автоматического и динамического баланса нагруженности, расширяемости и способности к самовосстановлению.
Многоагентная система для параллельного программирования
Многоагентные системы и роевой интеллект
Где можно применять мультиагентные системы.
Благодаря тому, что структура мультиагентных систем очень близка структурам реального мира, область применения МАС очень широка:
| Jade | Coguaar | Aglobe | Jason | breve | |
| область применения | мобильные сети, web, планирование и логистика, исследования технологии агентов | мобильные сети, web, промышленное применение, военное применение, огромные распределенные системы | промышленное применение, моделирование инженерных систем | Исследовательские проекты | Виртуальные миры, искусственная жизнь |
| технологии | Java SE, Java, поддерживает стандарты FIPA | Java SE, Java ME | Java SE | Java SE | |
| расширяемость | возможность расширения на всех уровнях | возможность расширения на всех уровнях | нет | есть | есть |
| наличие плагинов | большое количество | большое количество | нет | есть | нет |
| интеграция | Java EE (JMS, Web...), CORBA, | Java EE (JMS, Web...), CORBA, | Отсутствует | Saci, Jade | — |
| наличие дополнительной документации | + | — | + | + | |
| лицензия | LGPL | open-source (BSD-based) License | CPL | LGPL | open-source License |
| методология | — | — | — | — | — |
| наличие средств визуализации | — | — | + | — | + |
| инструментарий разработчика | поддерживаются основные этапы разработки |
поддерживаются основные этапы разработки |
минимальный | поддерживаются основные этапы разработки |
минимальный |
Существуют многочисленные многоагентные подходы (роевая оптимизация и близкие методы) к решению задач дискретной
оптимизации. Из них наиболее известны генетические алгоритмы, алгоритм муравьиной колонии и метод роя частиц. Менее
известны алгоритм пчелиной колонии, искусственные иммунные
системы, алгоритмы разумных капель, алгоритм кукушки и другие алгоритмы, основанные на биологических и физических метафорах. Данные подходы хорошо исследованы и им посвящено большое количество обзоров, например [61]. Однако следует
отметить, что наблюдается тенденция к злоупотреблению подобными метафорами, когда под экзотической аналогией скрывается
уже хорошо известный метод [32].
В механике твердого тела, в механике жидкости и газа существуют подходы, в которых среда рассматривается как множество последовательно движущихся по дискретной решетке или
сталкивающихся фиктивных частиц, т.е. как клеточный автомат.
Примерами таких методов является movable cellular automaton
(MCA, [10]), Lattice Gas cellular automata и Lattice Boltzmann
methods (LBM).
Пусть 𝑓𝑖(⃗𝑥, 𝑡) – одночастичная функция распределения, дающая вероятность нахождения частицы со скоростью ⃗𝑣𝑖 в клетке
⃗𝑥 в момент времени 𝑡. Скорость ⃗𝑣𝑖 может принимать значение
из некоторого конечного множества, зависящего от типа решетки, например 
= (cos(2𝜋𝑖/6),sin(2𝜋𝑖/6)) для гексагональной
сетки. Функция перехода клеточного автомата в LBM обычно состоят из двух шагов вида:
1. Релаксация (также говорят «шаг коллизий»)
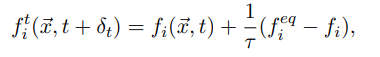
где
– вектор координат клетки в решетке;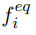 
– локальная функция равновесия, аппроксимирующая распределение Больцмана
(𝑅 – универсальная газовая постоянная; 𝑇 – температура; 𝜌 – плотность среды; 𝑢 – макроскопическая скорость газа; 𝐷 – размерность пространства); 𝜏 – время
релаксации; 𝛿𝑡 – шаг дискретного времени.
2. Распространение потоков:
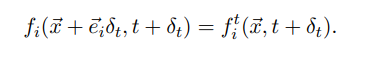
Рис. 2. Тактовое функционирование клеточного автомата
для LBM вида 𝐷2𝑄9
В работе С. Вольфрама [66] рассматривается применение
LBM к моделям жидкостей, описываемых уравнениями Навье–
Стокса. Отметим, что в этих моделях применяют автоматы с треугольными, квадратными, шестиугольными и другими ячейками.
Общая схема классификации моделей имеет вид 𝐷𝑛𝑄𝑚. Здесь
𝐷𝑛 – это размерность 𝑛 решетки, 𝑄𝑚 – количество 𝑚 соседей
для клетки, включая ее саму. Преимуществом данных методов
над традиционными методами вычислительной механики является легкость применения параллельных вычислений. Существуют специализированные обзоры таких подходов, составленные
специалистами по механике (например, [63]), автору же данного
обзора хочется отметить, что именно клеточные автоматы, первоначально описывающие динамику газа, породили многие из моделей поведения толпы.
Биомедицинские многоагентные модели обычно напоминают модели из предыдущего подраздела. В качестве клеток клеточного автомата в модели обычно берутся живые клетки. Например, в статье [13] описан двухмерный клеточный автомат (рис. 3),
моделирующий развитие опухоли. В качестве ячеек автомата рассматриваются нормальные и опухолевые клетки, а функция перехода автомата учитывает уровень насыщенности кислородом,
близость клетки к сосуду и разное поведение нормальных и раковых клеток. Показывается, что ток крови и неоднородность красных кровяных телец играют главные роли в развитии таких колоний клеток, даже когда красные кровяные тельца проходят через
сосуды в нормальной, здоровой ткани.
Правила эволюции вышеуказанного клеточного автомата таковы:
1. Пустой или занятый сосудом элемент не развивается, за
исключением случая, когда в соседнем занятом элементе происходит деление клетки.
2. Распределение кислорода рассчитывается путем решения
соответствующей краевой задачи
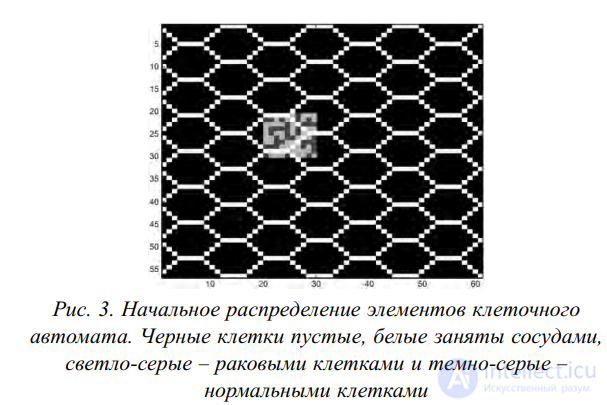
Рис. 3. Начальное распределение элементов клеточного
автомата. Черные клетки пустые, белые заняты сосудами,
светло-серые – раковыми клетками и темно-серые –
нормальными клетками
где 𝑃 – распределение внеклеточного кислорода, 𝐷𝑃 – коэффициент диффузии, 𝑘(⃗𝑥) – скорость потребления кислорода в позиции
⃗𝑥, n𝑤 – вектор внешней к стенке сосуда единичной нормали, 𝒫
– проницаемость сосуда, 𝑃𝐵 – уровень кислорода внутри сосуда,
n|∂Ω – вектор внешней единичной нормали к границе области.
Величина 𝑘(⃗𝑥) обновляется на каждом шаге функционирования
клеточного автомата и зависит от клеток в позиции ⃗𝑥.
3. Тип клетки в занятом элементе хранится в векторе состояния. Клетки пытаются делиться на каждом шаге.
4. Правила процесса деления зависят от типа клетки. Для
нормальной клетки определяется локальная концентрация кислорода. Если концентрация кислорода ниже порогового значения,
клетка погибает, в противном случае пытается делиться. Пороговое значение определяется по состоянию ближайших соседей.
Если клетка окружена по большей части нормальными, а не раковыми клетками, то фиксируется пороговое значение 𝑁𝑇1, в противном случае фиксируется 𝑁𝑇2 > 𝑁𝑇1.
Правила для раковых клеток аналогичны правилам для нормальных клеток, за исключением того, что сравнение между
уровнем кислорода и пороговым значением определяет только то, будет ли клетка делиться. Правила гибели раковой клетки определяются по-другому. Если с клеткой соседствует больше раковых
клеток, чем нормальных, тогда для нее фиксируется пороговое
значение 𝐶𝑇1, в противном случае фиксируется 𝐶𝑇2 > 𝐶𝑇1.
Неравенства 𝐶𝑇1 < 𝐶𝑇2 и 𝑁𝑇1 < 𝑁𝑇2 означают, что клетки с
большей вероятностью делятся, если они, в основном, окружены
клетками того же типа.
5. Элементы, занятые раковыми клетками, в которых локальная концентрация кислорода ниже порогового, входят в покоящееся состояние, в течение которого большая часть функций клетки
приостанавливается, включая пролиферацию. При входе в это состояние запускается таймер, увеличивающийся на единицу каждый шаг, когда ячейка остается в состоянии покоя. Если таймер
достигает заданного значения, клетка погибает. Однако, если в
какой-то момент уровень кислорода перейдет выше порогового
значения, ячейка вернется к размножающемуся состоянию, а ее
таймер сбросится до нуля.
6. Элементы, занятые нормальными и раковыми клетками,
являются потребителями кислорода.
7. Если уровень кислорода в элементе, занятом клеткой, выше порога, то клетка будет делиться, если в ее окрестности радиуса 𝑅 есть пустые элементы. Если свободное место есть, то новая
клетка переходит в свободный элемент с наибольшей концентрацией кислорода. Иначе клетка не может делиться и погибает.
Модель роста опухоли в статье [44] также основана на клеточном автомате, подобном вышеупомянутому, но учитывает генетические особенности злокачественных клеток, делающих их
нечувствительными к сигналам прекращения роста, выключающими программу клеточной смерти (апоптоза) и т.п.
В статье [45] моделируется процесс функциональной адаптации костной ткани с помощью гибридного (т.е. сочетающего
дискретные и непрерывные правила) клеточного автомата, подобного используемым в механике твердого тела.
В статье [24] приведена простая многоагентная модель эпидемии. Модель была предназначена для исследования влияния та19
Управление большими системами. Выпуск 71
ких факторов, как начальное количество инфицированных, плотность популяции и максимальное количество клеток, через которое может распространяться инфекция. Далее это направление
исследований получило определенную популярность и сейчас
существуют агентные модели эпидемии, учитывающие образцы
человеческого поведения, полученные из реальных данных, мобильность и т.д., например, [22].
Многоагентный подход применяется в неклассических вычислениях, например, в биологических вычислениях. Слизевик
Physarum polycephalum (гигантское многоядерное одноклеточное
существо, рис. 4) часто применяется как модельный организм для
биологических вычислений, который может быть запрограммирован различными внешними стимулами. В ответ на эти стимулы он растет, меняет конфигурацию, выпускает ложноножки и
т.п. [30], что и кодирует определенные операции над числами,
помимо этого слизевик способен к обучению и самообучению.
Например, в свое время этот слизевик был использован в качестве системы управления роботом, избегающим света.
Рис. 4. Physarum polycephalum на стволе дерева (фотография
frankenstoen – flickr, CC BY 2.5,
Существует сайт http://www.phychip.eu/, посвященный проекту PhyChip – построению вычислительной системы на основе
слизевиков Physarum. В статье [29] рассматривается многоагентная среда, симулирующая поведение Physarum polycephalum.
Поведение слизевиков привело к созданию моделей движения толпы [33]. Предлагается основанная на клеточном автомате
модель Physarum, которая имитирует процесса поиска и диффузии пищи, роста организма, создания ложноножек для каждого
организма. При этом выбору оптимального пути эвакуацией толпы соответствует оптимальный выбор ложноножки моделируемого организма Physarum.
Также существуют связанные с поведением слизевиков модели из различных видов неклассической логики и теории игр
[55, 57, 58]. В статье [56] рассматривается клеточные автоматы
с правилами, меняющимися на каждом ходу. Используя эти автоматы, возможно формализовать рефлексивные игры на основе
контекста для 𝑘 игроков на разных конечных или бесконечных
уровнях рефлексии. Каждый игрок имеет собственное правило
принятия решения, определяемое логической функцией на своих выигрышах в контексте, который постоянно изменяется. Это
правила нулевого уровня рефлексии. Если игрок 1 следует правилу принятия решения, которое является логической комбинацией
с решающим правилом игрока 2 нулевого уровня рефлексии, то
мы говорим, что правило решения игрока 1 относится к первому
уровню. Между тем, если игрок 2 следует правилу принятия решения, которое является логической комбинацией с решающим
правилом игрока 1 первого уровня рефлексии, то говорится, что
правило решения игрока 2 относится к второму уровню и т.д.
В работе [59] рассматривается роевое поведение алкоголиков
с точки зрения неклассической логики. В качестве роев рассматриваются небольшие группы собутыльников. Было обнаружено,
что алкоголики образуют сеть, состоящую из нескольких небольших групп. Задача оптимизации обычных напитков решена не
небольшой группой, а всей сетью, т.е. несколькими группами,
члены которых взаимосвязаны.
Дело в том, что каждая небольшая группа алкоголиков появляется и исчезает в разных условиях, но сеть, к которой относятся эти алкоголики, остается практически постоянной. Оказалось, что небольшие группы лиц, страдающих алкоголизмом,
нестабильны и, обмениваясь своими членами, могут слиться или
разделиться для оптимизации потребления алкоголя. Те же поведенческие закономерности наблюдаются у слизевиков: сплавление и расщепление перед аттрактантами для оптимизации их
захвата.
Внешние стимулы (аттрактанты) для слизевиков представляют собой кусочки питательных веществ, разбросанных перед
этим организмом. Аттрактанты для алкоголиков представлены
местами, где они могут спокойно пить в небольших группах. 38%
респондентов предпочитают пить в одном месте и 62% в разных
местах. Аргументы при выборе мест следующие: короткое расстояние от дома, низкая цена, качество напитков.
Агентные (микроскопические) модели применяются для моделирования транспортных потоков, обычно однополосных. В
основе подходов лежит концепция «о желании придерживаться при движении безопасной дистанции до лидера». В монографии приводятся, например, модель оптимальной скорости Нагеля–Шрекенберга, основанная на клеточных автоматах,
которая является простейшей. В этой модели на каждом шаге
𝑚 → 𝑚 + 1 состояние всех автотранспортных средств в системе обновляется в соответствии со следующими правилами (здесь
𝑣𝑛 6 𝑣max – скорость, а 𝑠𝑛 – координата 𝑛-го транспортного средства):
1) ускорение (отражает тенденцию двигаться как можно быстрее, не превышая максимально допустимую скорость):
𝑣𝑛(𝑚 + 1) = min{𝑣𝑛(𝑚) + 1, 𝑣max};
2) торможение (гарантирует отсутствие столкновений с впереди идущими автотранспортными средствами):
𝑣𝑛(𝑚 + 1) = min{𝑣𝑛(𝑚), 𝑠𝑛+1(𝑚) − 𝑠𝑛(𝑚) − 𝑑},
где 𝑑 ∼ 7,5 м;
3) случайные возмущения (учитывают различия в поведении
транспортных средств):
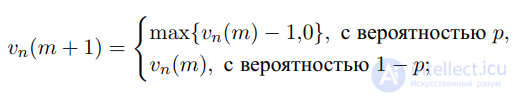
4) движение:
𝑠𝑛(𝑚 + 1) = 𝑠𝑛(𝑚) + 𝑣𝑛(𝑚).
В работе [35] приводятся модели кратковременной динамики
следования за лидером, которые описывают непрерывные задачи
обратной связи (ускорение и торможение) и задачи дискретного выбора как ответ на окружающий транспортный поток. Стиль
вождения агентов характеризуется параметрами модели – временем реакции, желаемой скоростью и т.п. Также используются переменные внутреннего состояния, соответствующие уму агента,
для описания опыта водителя. На поведение водителя действуют
соседние транспортные средства и другие внешние воздействия.
Предположительно самая первая работа, описывающая
агентный подход к моделированию роя или стаи, – это статья
Рейнольдса [52]. В ней выделено три основных принципа построения роя:
Автор предлагал применять вышеизложенные принципы для
графического отображения роя частиц, но вскоре они нашли и
другие применения.
В работе [31] использован двухмерный клеточный автомат
(так называемый world-space cellular automaton, рис. 5, изображение из цитируемой ниже работы Ross Mead) с правилами, близкими к Game of Life Конвея, симулирующий образование роя
(swarm) агентов с помощью поля социального потенциала. Агенты отталкиваются друг от друга, если слишком сильно приблизятся или притягиваются, если находятся достаточно далеко друг
от друга. Сила отталкивания и (или) притяжения между двумя
агентами описывается как
,
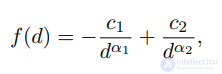
где 𝑐1 , 𝑐2 > 0 , 𝛼1 > 𝛼2 > 0 – параметры агентов, 𝑑 – расстояние
между агентами. Если агент 𝐴 обнаруживает соседей 𝑁1, . . . 𝑁𝑘
на расстояниях 𝑑1, . . . , 𝑑𝑘, то сила, примененная к агенту 𝑖 соседом 𝑁𝑖 будет
.
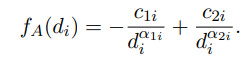
Суммарная сила, примененная к агенту 𝐴 будет
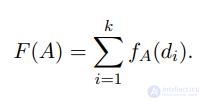
Предполагалось использование миниатюрных роботов, снабженных сенсорами и системой связи, с таким поведением при
ликвидации чрезвычайных ситуаций.
Так вышло, что самая первая работа по моделированию движения группы людей, которую автор настоящего обзора прочел
и которая определила его интерес к агентным системам – этостатья .
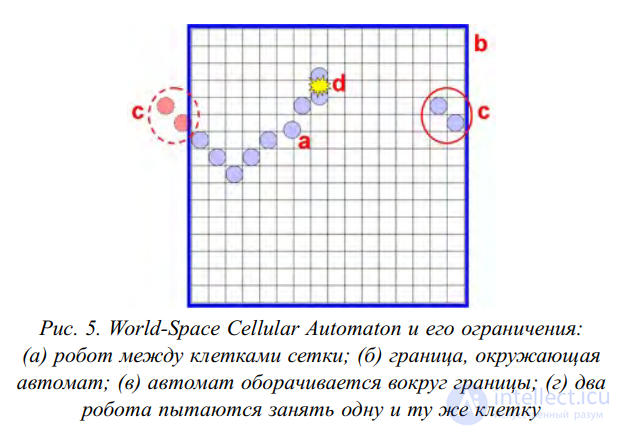
Рис. 5. World-Space Cellular Automaton и его ограничения:
(а) робот между клетками сетки; (б) граница, окружающая
автомат; (в) автомат оборачивается вокруг границы; (г) два
робота пытаются занять одну и ту же клетку
В ней применяется клеточный автомат с вероятностной локальной функцией перехода, изначально предложенный
для моделирования динамики газов, для построения модели движения неорганизованной группы людей между препятствиями,
например, между ограждениями в метро.
Следует отметить, что в России сложилась своя собственная школа математического моделирования поведения толпы, и
стоит упомянуть в связи с этим монографию , посвященную
математическим моделям управления толпой, поведение которой
описывается как пороговое (конформное) коллективное принятие
решений ее элементами.
Стоит отметить, что для данного направления характерно,
что одни и те же результаты используются и для моделирования
строя агентов на компьютере, и для проектирования искусственного интеллекта наземных роботов и БПЛА.
В [16, 39, 41, 42] и других работах того же коллектива авторов описан алгоритм, позволяющий организовывать
строй (formation) агентов, определенный с помощью одной или
нескольких математических функций. Формация агентов рассматривается как одномерный клеточный автомат (так называемый robot-space cellular automaton), каждая клетка которого содержит координаты агента на плоскости, его реальное и желаемое взаимное расположение с соседними агентами (см. рис. 6).
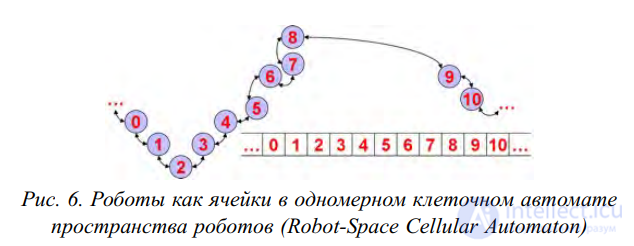
Рис. 6. Роботы как ячейки в одномерном клеточном автомате
пространства роботов (Robot-Space Cellular Automaton)
Каждый агент (робот) представим клеткой 𝑐𝑖 одномерного клеточного автомата. Каждая клетка имеет окрестность
{𝑐𝑖−1, 𝑐𝑖, 𝑐𝑖+1}. Пусть желаемая формация задана функцией 𝑓(𝑥),
которая известна одному из агентов 𝑐𝑠𝑒𝑒𝑑 и каждый агент 𝑐𝑖 знает
свои координаты 𝑝𝑖. Желаемое отношение 𝑟𝑖→𝑗,𝑑𝑒𝑠 между 𝑐𝑖 и 𝑐𝑗
определяется как вектор с началом в 𝑝𝑖 и концом в точке пересечения 𝑓(𝑥) и окружности радиуса 𝑅 с центром в 𝑝𝑖
, 𝑅 – это желаемое расстояние между агентами. Используя данные сенсоров,
агент выясняет действительное отношение 𝑟𝑖→𝑗,𝑎𝑐𝑡. Данные о
желаемой формации, заданной через 𝑓(𝑥), распространяются локально от 𝑐𝑠𝑒𝑒𝑑 к соседям и от них далее. Все агенты вычисляют
свои желаемые и действительные отношения с соседями и движутся таким образом, чтоб минимизировать ‖𝑟𝑖→𝑗,𝑑𝑒𝑠 − 𝑟𝑖→𝑗,𝑎𝑐𝑡‖.
Агенты (наземные роботы) могут сохранять как уже созданный
строй, так и создавать новый. Демонстрируется работа алгоритма на примере колесных роботов, распознающих друг друга по
цветным штрих-кодам и общающихся по радиосети XBee.
В работе [34] для решения сходной проблемы применен иной
подход. Желаемый строй агентов задан графом и задача построения строя сводится к деформации взвешенного графа, описывающего исходное расположение агентов, к желаемому виду, с
учетом ограничений по возможностям связи агентов друг с другом (7). При этом необходим поиск изоморфизма между желаемым и существующим графом строя. Координаты агентов с номером 𝑖 задаются как обыкновенное дифференциальное уравнение
вида (т.н. интегратор первого порядка)
где 𝑞𝑖 – координаты агента, а 𝑢𝑖 – его скорость, являющаяся в
данном случае управлением.
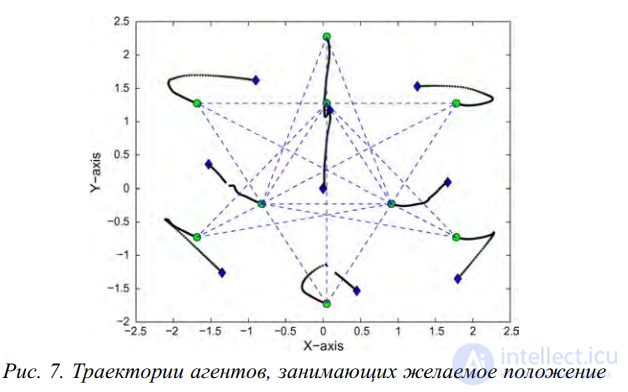
Рис. 7. Траектории агентов, занимающих желаемое положение
Статья описывает построение строя роботов во многом
аналогично ранее цитированной статье, однако, предлагаемый в
работе подход корректно обрабатывает ситуации возможной поломки, присоединения новых агентов к строю и смены положения цели, работоспособность подхода проверена при помощи
компьютерного моделирования. Также проанализирована работа
алгоритма в условиях введения ошибки измерений и при наличии
препятствий.
В статье также решается задача управления формациями,
а именно задача обобщения алгоритма равноудаленного распо27
Управление большими системами. Выпуск 71
ложения агентов на заданном фиксированном отрезке. Показана
связь между задачей расположения на отрезке и классической
задачей достижения консенсуса. Поведение агентов здесь описывается, из соображений большей физичности модели, интеграторами второго порядка:
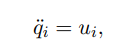
где 𝑞𝑖 – координаты агента, а 𝑢𝑖 – его ускорение, являющаяся в
данном случае управлением.
Работа [20] описывает построение такого строя БПЛА, который позволял бы поддерживать сеть связи БПЛА в максимально
связном состоянии. Положения агентов задаются системой дифференциальных уравнений и задача рассматривалась с точки зрения теории устойчивости.
Довольно большой обзор по задачам построения строя приведен в [46].
В этом направлении существуют два (возможно пересекающихся) класса агентных моделей. Один из них описывает построение реального протокола связи внутри телекоммуникационной
сети, а второй предназначен для компьютерных симуляций телекоммуникационных сетей.
В одном из ранних обзоров [64] перечисляются различные
многоагентные модели построения сетей связи. В качестве агентов рассматриваются, естественно, сами узлы телекоммуникационной сети (рис. 8), при этом для таких агентов также может
применяться модель BDI. Приводятся примеры распределенного
и децентрализованного управления сетью, муравьиных алгоритмов маршрутизации и прочие решения, основанные на агентном
подходе. Многие из них сохраняют актуальность и развиваются
и по сей день.
В статье [43] было, вероятно, впервые описано применение
многоагентного подхода к моделированию сети связи. В статье
указывалось, что такие традиционные модели телекоммуникационной сети, как теория очередей, сети Петри или исчисление процессов, не вполне подходят для представления мобильных сетей
или основанных на применении политик (policy-based) сетей, так
как приводят к сложным и трудноразрешимым уравнениям, игнорируют индивидуальное поведение узлов и требуют задания
ограниченного числа возможных состояний сети.
Рис. 8. Пример структуры агента телекоммуникационной сети
Моделировалась система связи с сообщениями трех классов по QoS и пятью типами поведения узлов, включающими поведение узлов с
динамической и статической маршрутизацией, а также разными
способами построения очереди сообщений.
В связи с появлением концепции «интернета вещей» многоагентные системы как основа для разработки [38] и моделирования [15] сети связи становятся все более актуальными. В
этом случае реальным прототипом агентов являются смартфоны,
встраиваемые сетевые устройства и т.п., оснащенные специальными программными компонентами, позволяющими отображать
в Web данные, задачи и службы всей системы агентов.
В работе решается задача, во многом аналогичная задаче
построения строя агентов, однако в ней с помощью графа задается не пространственные взаимоотношения между агентами, а
желаемая форма сети связи. Агенты, обмениваясь сообщениями
о фрагментах желаемой системы связи, организуют каналы связи со своими соседями в соответствии с полученными данными
так, чтоб разница между желаемым и возможным для построения
фрагментом графа связи была минимальным.
Многоагентные модели применяются при моделировании
боевых действий, особенно современных локальных конфликтов (так называемых stability operations), для которых оказались
не применимыми традиционные модели, оперирующие, главным
образом, некоторыми интегральными показателями для больших военных соединений. С конца 1990-х – начала 2000 гг.
получили определенную известность среды моделирования конфликта ISAAC и EINSTein, разработка US Marine Corps Combat
Development Command. В монографии [28] дано подробное описание алгоритмов и интерфейсов вышеуказанных систем, а также исследованы различные феномены типа самоорганизующейся
тактики агентов.
Также известны, например, модель Map Aware Non-uniform
Automata (MANA), разработанная Operations Analysis group в
Defence Technology Agency (DTA), Новая Зеландия или же
Pythagoras – разработка Marine Corps Warfighting Laboratory министерства обороны США [40, 53]. Кроме того, конфликты моделируют и в средах агентного моделирования общего назначения
типа NetLogo.
Помимо упомянутых систем, автором настоящего обзора была разработана программа моделирования движения и боевых
действий иерархически организованных агентов «Бокоход» (номер свидетельства о государственной регистрации Роспатентом
2016615934), которая имела в своей основе алгоритм, близкий к
описанному в [28]. Данный алгоритм изложен в работе [37], и, в
отличие от ранее упомянутых алгоритмов ISAAC, сфокусирован,
главным образом, на конфликте агентов в условиях неизвестного и, возможно, постоянно изменяющегося окружения, состоя
щего из ячеек разной степени проходимости. Для этой цели в
программе «Бокоход» реализован поиск локально-оптимальных
маршрутов агентов. Также используется особый математический
формализм, в котором агент не является отдельной от среды сущностью, а является частью состояния ячейки world-space cellular
automaton, моделирующего окружающую среду. В результате этого достигается определенный прирост производительности программы. При этом если имеется несколько агентов, претендующих на одну ячейку, ячейка разыгрывается между ними по определенному алгоритму.
Наконец, многоагентное моделирование применяется и в
социально-экономических науках. Применение таких моделей в
экономике стало распространенным, по всей вероятности, после
мирового финансового кризиса 2008 г., как утверждается в монографии [25]. Преимущество агентного моделирования в том,
что оно хорошо отражает сложность взаимоотношений различных людей, домохозяйств и фирм в динамике. Агентное моделирование позволяет непосредственно связать микроуровень и макроэкономическую ситуацию и не требует равновесия экономической системы.
При этом следует отметить, что обзорные статьи на тему
применения агентного моделирования в экономике появились намного раньше, как, например статья [48], изданная в виде отчета
еще в 2005 г.
Агентные модели используются и для описания социальных
сетей, как естественно и давно существующих в обществе, так
и для компьютерных социальных сетей. Например, работа [12]
предлагает многоагентную модель добавления «друзей» в социальной сети Facebook, построенную по результатам анализа
данных студентов Калифорнийского технологического института
(Caltech).
В работе [47] приведен большой обзор (по сути, учебник)
моделей динамики мнений в социальных сетях. Рассматриваются
предложенные в 1950–90 гг. модель эволюции мнений Френча–де Гроота
𝑥(𝑘 + 1) = 𝑊 𝑥(𝑘), 𝑘 = 0, 1, . . . ,
где 𝑊 = (𝑤𝑖𝑗 ) – 𝑛 × 𝑛 матрица весов влияния, 𝑤𝑖𝑗 > 0, модель Абельсона
где 𝐿[𝐴] – матрица Кирхгофа, модель Фридкина-Джонсена
𝑥(𝑘 + 1) = Λ𝑊 𝑥(𝑘) + (𝐼 − Λ)𝑢,
где Λ = 𝑑𝑖𝑎𝑔(𝜆1, . . . , 𝜆𝑛), где 𝜆𝑖 ∈ [0, 1] означает восприимчивость 𝑖−го агента к процессу социального влияния, 𝑢 – постоянный вектор предубеждений агентов, и Тэйлора
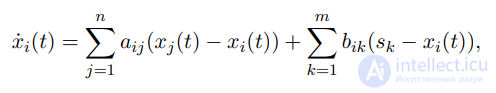
где 𝐴 = (𝑎𝑖𝑗 ) – 𝑛×𝑛 матрица весов, 𝐵 = (𝑏𝑖𝑘) – 𝑛× 𝑚 неотрицательная матрица «констант убедительности». Также исследуется
взаимосвязь этих моделей с современными многоагентными моделями.
В статье [23] исследуется поведение группового консенсуса,
который зависит от нескольких утверждений, одно из которых
является ложным. Показывается, как существование логических
ограничений на убеждения влияет на коллективную сходимость
к общей системе убеждений и, напротив, на то, как набор произвольно связанных убеждений, разделяемых меньшинством, может стать разделяемым большинством. В качестве примера рассматривается динамика мнений жителей США относительно ввода войск в Ирак при изменении их уверенности в утверждениях
1. У Саддама Хусейна есть запас оружия массового уничтожения.
2. Оружие массового уничтожения у Саддама Хусейна является реальным и представляет опасность для региона и всего мира.
3. Упреждающее вторжение в Ирак является справедливой войной.
Математической моделью динамики убеждений является
обобщение модели Фридкина–Джонсена.
𝑋(𝑘 + 1) = 𝐴𝑊 𝑋(𝑘)𝐶⊤ + (𝐼 − 𝐴)𝑋(0), 𝑘 = 0, 1, . . . ,
где 𝑋(𝑘) – 𝑛×𝑚 матрица позиций 𝑛 индивидуумов по 𝑚 взаимозависимым вопросам; 𝑊 = (𝑤𝑖𝑗 ) – 𝑛×𝑛 матрица весов влияний;
𝐴 = (𝑎𝑖𝑗 ) – диагональная 𝑛×𝑛 матрица со значениями на главной
диагонали 𝑎𝑖𝑖 = 1−𝑤𝑖𝑖, 𝑖 = 1, 𝑛; 𝐶 – 𝑚×𝑚 матрица зависимостей
между вопросами; 𝐼 – 𝑛 × 𝑛 тождественная матрица. В данной
модели консенсус может не достигаться
роевой интеллект
А как ты думаешь, при улучшении многоагентная система, будет лучше нам? Надеюсь, что теперь ты понял что такое многоагентная система, многоагентные системы, мультиагентные системы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Интеллектуальные агенты . Многоагентные системы
Комментарии
Оставить комментарий
Интеллектуальные агенты . Многоагентные системы
Термины: Интеллектуальные агенты . Многоагентные системы