Лекция
Привет, Вы узнаете о том , что такое флаттер, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое флаттер, задача келдыша, бафтинг, эффект шимми , вобблинг , настоятельно рекомендую прочитать все из категории Аэродинамика.
флаттер (англиц. от flutter «дрожание, вибрация») — сочетание самовозбуждающихся незатухающих изгибающих и крутящих автоколебаний элементов конструкции летательного аппарата: главным образом, крыла самолета либо несущего винта вертолета. Как правило, флаттер проявляется при достижении некоторой критической скорости, зависящей от характеристик конструкции летательного аппарата; возникающий резонанс может привести к его разрушению. Переход к сверхзвуковым скоростям осложнялся опасностями флаттера.
Флаттер – это автоколебания твердого тела или системы механически связанных между собой твердых тел в потоке сплошной среды, то есть жидкости или газа, вместе с этой средой. Этим флаттер отличается от других видов автоколебаний, происходящих в сплошных средах, при которых твердые тела остаются неподвижными, по крайней мере, на начальной стадии и в теоретических моделях этих процессов. Как у любого автоколебательного процесса, у флаттера должен иметься механизм положительной обратной связи, который обеспечивает перекачку энергии к нему из окружающей среды. По типу этого механизма можно выделить изгибно-крутильный флаттер, «многозвенный» (в авиации наиболее типичный его вариант называют изгибно-элеронным) [20] и срывной флаттер.
Значения поятия флаттера
Связанне понятия
Автоколебания — незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счет энергии постоянного, то есть непериодического внешнего воздействия.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Термин автоколебания в русскоязычную терминологию введен А. А. Андроновым в 1928 году.
бафтинг (англ. buffeting, от buffet — ударять, бить) — один из видов автоколебаний, представляющий собой вынужденные колебания всей конструкции или ее частей, вызванные периодическим срывом турбулентных вихрей с расположенных впереди конструктивных элементов при их обтекании .
Для летательных аппаратов бафтинг чаще всего проявляется как резкие неустановившиеся колебания хвостового оперения, вызванные аэродинамическими импульсами от спутной струи воздуха за крылом.
эффект шимми ( вобблинг ) (англ. wobble, speed wobble, tank-slapper, death wobble ) — возникновение быстрых колебаний (частотой 4…10 Гц), как правило, на рулевых колесах транспортного средства. В момент возникновения шимми транспортное средство в целом не подвержено влиянию колебаний, однако с нарастанием их амплитуды происходит потеря управления из-за усиливающегося рыскания. Угроза развития шимми, теоретически, существует у любых транспортных средств с одной точкой приложения управляющего воздействия при наличии достаточной степени свободы рулевого колеса, например, мотоциклы, велосипеды и скейтборды, а, кроме того, трехколесные легкие самолеты, способные на земле развивать скорость свыше 80 км/ч. На большинстве автомобилей эффект шимми существенно не проявляется. Нестабильность, предшествующая развитию эффекта, возникает, как правило, на больших скоростях и по ощущениям примерно соответствует характерным колебаниям колес магазинных тележек или поведению самолетного шасси во время приземления
Причиной флаттера обычно является несовпадение центра жесткости с центром давления и недостаточная жесткость конструкции крыла.
Исследования флаттера в России начались в середине 1930-х годов. Советская авиация столкнулась с тем, что при увеличении скорости, при некотором критическом ее значении, самолеты начинало сильно трясти и они разрушались в воздухе. Вибрация нарастала настолько быстро, что у летчика не оставалось времени на снижение скорости. От начала вибраций до разрушения самолета проходили считанные секунды.
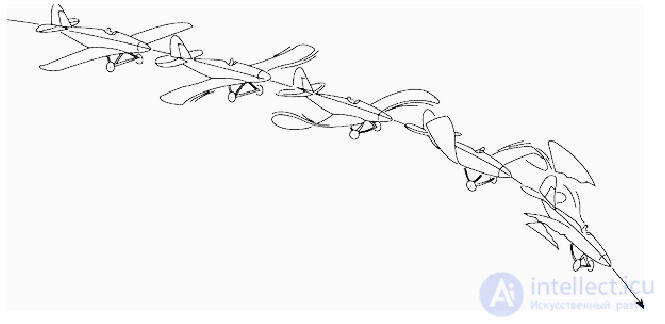
Над явлением флаттера ломали голову многие математики. Огромный вклад в решение проблемы внесли Е. П. Гроссман и М. В. Келдыш. Был поставлен целый ряд экспериментов, сделан ряд теоретических исследований, были разработаны практические приемы для исключения вибрации при любой скорости полета. Основным результатом работ, проведенных в СССР в 1934—1941 годах, было устранение опасности появления флаттера крыла и оперения. Опираясь на исследования Келдыша, авиаконструкторы избавились от флаттера, и жизни многих летчиков были спасены.
М. В. Келдыш, занимаясь задачей нелинейного анализа математических моделей подавления флаттера органов управления самолета, использовал метод гармонического баланса и отмечал, что «мы не даем строгого математического доказательства всех относящихся сюда положений, а ряд выводов построим на интуитивных соображениях» . Последующее развитие теории абсолютной устойчивости, теории дифференциальных включений, а также аналитических и численных методов их анализа, недоступных Келдышу во время его работы, позволяет в настоящее время проводить строгий анализ устойчивости и возникновения скрытых колебаний в моделях Келдыша .
Виды флаттера в зависимости от наличия перемещений и вибрации органов управления:
Виды флаттера в зависимости от элемента, подверженного перемещениям и деформации:
В зависимости от того, какие элементы конструкции подвергаются перемещениям и деформации, различают многие типы флаттера, в том числе:
1) Изгибно-крутильный крыла (крыло гнется и скручивается),
2) Изгибно-элеронный (крыло гнется, элерон отклоняется),
3) Крутильно-элеронный (крыло скручивается, элерон отклоняется),
4) Изгибно-элеронно-триммерный (крыло гнется, элерон и триммер отклоняются),
5) Серво-компенсаторный,
6) Хордовый флаттер лопастей несущего винта вертолета.
Флаттер крыла может возникнуть под воздействием какой-либо силы (отклонение элерона, порыв ветра), вызвавшей отклонение крыла за счет его изгиба из исходного (нейтрального) положения 1 (из плоскости 0XZ), например, вверх. Об этом говорит сайт https://intellect.icu . Стремясь под действием сил упругости вернуться в исходное положение, крыло начнет двигаться вниз (2) не плоскопараллельно, но с закручиванием из-за несовпадения положений центра давления (в котором приложена подъемная сила) и центра масс (в котором приложены инерционные и массовые силы) с центром жесткости (относительно которого происходит закручивание крыла).
Проскочив по инерции нейтральное положение, крыло отклонится вниз (3, 4), и картина повторится с изменением знаков всех сил и моментов.
Фазы этого движения и соответствующие им изгибно-крутильные (
– изгибные и 
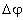– крутильные) деформации крыла за один цикл колебаний относительно исходного положения (плоскости 0XZ) проиллюстрированы рисунком.
Рис Иллюстрация явления флаттера крыла самолета
Флаттер моста
В изгибно-крутильном флаттере положительная обратная связь реализуется, если линия центров инерции тела находится по потоку за линией центров жесткости, что при отсутствии специальных мер является типичной ситуацией для таких тел, как, например, крыло самолета. Тогда при изгибных колебаниях крыла оно закручивается так, что дополнительная аэродинамическая сила на нем, вызванная кручением, действует в ту же сторону, куда крыло движется во время своего маха, усиливая его. Таким образом, эти изгибные махи экспоненциально растут, усиливая сами себя, пока крыло не разрушится [20].
В «многозвенном» флаттере принимает участие система не менее чем из двух механически связанных твердых тел, на практике обычно крыла и элерона – отдельной небольшой аэродинамической поверхности, расположенной за основным крылом. При этом в отличие от бафтинга между телами рассматриваемой колебательной системы нет заметных пространственных промежутков (элерон, в отличие, скажем, от хвостового оперения, располагается непосредственно на крыле). В таком случае кручение крыла уже не обязательно, а источником положительной обратной связи является этот самый элерон, движущийся относительно крыла так, что создает дополнительную аэродинамическую силу системы крыло-элерон в направлении маха крыла [20]. В остальном механизм положительной обратной связи такой же, как и в предыдущем типе флаттера. Оба этих типа флаттера возникают на хорошо обтекаемых телах, когда в базовую математическую модель явления нет необходимости включать вязкость сплошной среды, а решение ищется для невязкого потенциального потока (потенциального везде, за исключением особых точек, число которых равно числу тел колебательной системы).
В отличие от кратко описанных выше типов флаттера, для появления и развития срывного флаттера, возникающего на плохообтекаемых телах, вязкость потока имеет принципиальное значение. Именно вследствие действия вязкости в потоке за такими телами возникают периодические структуры вихрей, называемые дорожками Кармана в честь выдающегося аэродинамика XX века Теодора фон Кармана, построившего первую адекватную математическую модель этого явления 98 лет назад. Сами дорожки Кармана с помощью простых методов визуализации, а иногда, даже и без них, можно наблюдать практически за любой преградой, возникающей на пути потока, как воздуха, так и воды (см., например, на рис. 6 фотографию 94 из источника [21], полученную при обтекании водой кругового цилиндра).
Рис. 6
Механизм положительной обратной связи при автоколебаниях тел, создающих такие дорожки, обеспечивается тем, что колебания тела усиливают вихреобразование, которое в свою очередь увеличивает силы и моменты, действующие на тело, и, следовательно, его колебания [22]. В отличие от изгибно-крутильного флаттера механизм перекрестного взаимодействия прямолинейного и крутильного движений элементов тела здесь не играет существенной роли, поэтому срывной флаттер может быть практически чисто изгибным (см. рис. 7, схематически изображающий дорожку Кармана в окрестности тела, моделирующего верхнее строение моста).
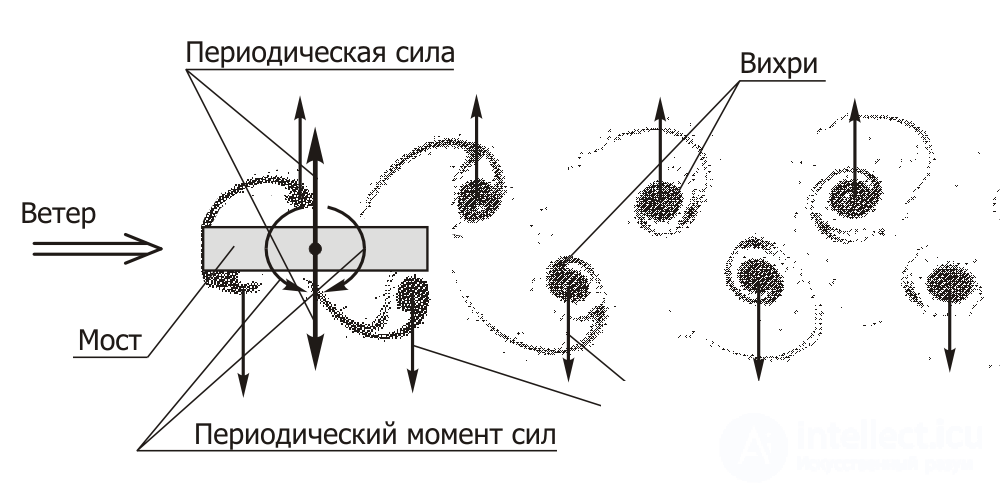
Рис. 7
При срывном флаттере на тело кроме подъемной силы, перпендикулярной направлению набегающего потока действует также и сила лобового аэродинамического сопротивления, направленная по потоку. Кроме постоянной компоненты сила сопротивления также имеет и колебательную вихревую компоненту, частота которой вдвое выше частоты вихревой подъемной силы. Разница частот возникает из-за того, что частота подъемной силы определяется расстоянием между вихрями только вдоль одной из сторон дорожки Кармана, а частота периодической компоненты лобовой силы определяется расстоянием между вихрями вдоль обеих ее сторон [22]. Переменная компонента лобовой силы обычно мала по сравнению с подъемной силой и, поэтому, на рис. 7 для простоты не показана.
Для наших целей нет необходимости подробно разбираться во всех тонкостях срывного флаттера, а достаточно использовать основные результаты теории этого явления. Частота появления вихрей νv при таком флаттере, которая является частотой возбуждения νp автоколебаний системы, вычисляется следующим образом:
(1)
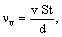
где St – число Струхаля (безразмерный параметр подобия), v – скорость потока, d – поперечный размер плохо обтекаемого тела. По существу формула (1) и является определением числа Струхаля, и поэтому, казалось бы, она не может являться рабочим инструментом для каких-либо вычислений.
Однако, имеется замечательное свойство таких срывных течений, заключающееся в том, что в очень широком и практически интересном диапазоне определяющих процесс параметров число Струхаля при заданной форме тела остается почти постоянным. Кроме того, даже там, где это число не постоянно, оно зависит только от единственной безразмерной их комбинации – параметра подобия, называемого числом Рейнольдса Re:
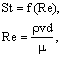
где ρ – плотность сплошной среды, μ – коэффициент ее динамической вязкости. На рис. 8, заимствованном из источника [23], показана зависимость числа Струхаля St от числа Рейнольдса Re при изменении последнего от 3·101 до 3·105 при обтекании кругового цилиндра, расположенного поперек потока.
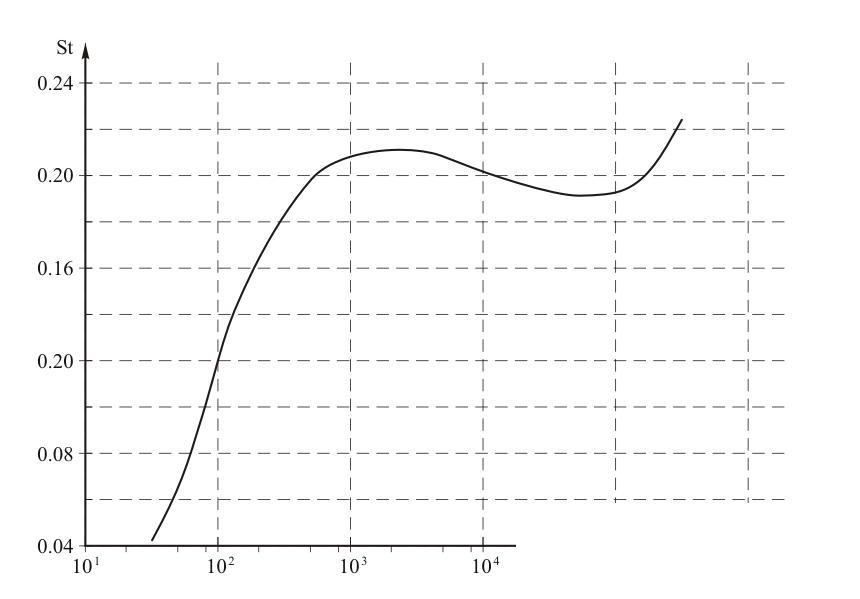
Рис. 8
Из графика видно, что при числах Рейнольдса от 3·102 < Re < 3·105 число Струхаля St = 0.20 ± 0.02. При скорости ветра 10 – 20 м/с и температуре воздуха около 290 К эти значения параметра подобия соответствуют диаметру цилиндра от 0.2 мм до 0.5 м (см. [24, 25]), что охватывает весь диапазон размеров от проволочек измерительных приборов и струн «эоловой арфы» до самых толстых вант подвесных мостов. При числах Рейнольдса 5·105 < Re < 5·106 дорожка вихрей за круговым цилиндром становится сильно турбулентной, так что число Струхаля становится невозможно определить. Далее, при Re > 5·106 число Струхаля снова стабилизируется и оказывается равным St ≈ 0.3 [22]. Все это относится к частоте возбуждения колебаний, направленных перпендикулярно скорости потока, то есть частоте подъемной силы вихрей. Если необходимо рассчитать обычно многократно более слабые колебания вдоль вектора скорости потока, то в числитель формулы (1) следует ввести множитель 2.
Есть еще одно свойство числа Струхаля при срывном флаттере, которое, может быть, даже еще более полезно для решения поставленной задачи – вычисления частоты возбуждения колебаний при ветровом обдуве мостов. Это его свойство заключается в том, что число Струхаля достаточно слабо зависит также и от формы поперечного сечения тела, особенно если на поверхности тела имеются ребра, фиксирующие положение отрывов, порождающих вихри. Из классического решения Кармана, выведенного для потока невязкого везде, за исключением двух точек на теле, и получаемого предельным переходом по числу Рейнольдса, следует, что для кругового цилиндра число Струхаля St ≈ 0.20 [26]. Из графика на рис. 8 следует, что эта величина хорошо согласуется с экспериментальными данными при 3·102 < Re < 3·105. Кроме цилиндра Карманом было рассмотрено обтекание еще одного тела – плоской пластинки, поставленной поперек потока [26]. Для нее обработка результатов расчетов и экспериментов привела к значению числа Струхаля St ≈ 0.145. Если поперечное сечение тела является квадратом, то число Струхаля для него будет практически такое же, как для пластинки – St ≈ 0.14 [27].
Единственным качественным отличием рассматриваемых зависимостей St = f(Re) для пластинки или тела с поперечным сечением типа прямоугольника, которое сразу можно предсказать, является то, что критическая величина числа Рейнольдса, при котором начинается сильно турбулентная зона, где число Струхаля невозможно определить, будет значительно больше, чем для кругового цилиндра, если эта граница для них существует вообще. Этот прогноз вызван тем, что при критической величине числа Рейнольдса Re* ≈ (1.5 – 3)·105, в случае обтекания трехмерного тела, в поперечном сечении совпадающим с круговым цилиндром, возникает явление, имеющее прямое отношения к рассматриваемым срывным течениям. Данное явление называется кризисом обтекания шара [28]. Оно обычно описывается как резкое падение аэродинамического сопротивления шара и вызвано быстрым, но неустойчивым стягиванием точек схода вихрей из периферийных районов поверхности шара ближе к его оси, параллельной набегающему потоку, вследствие перемещения точек отрыва пограничного слоя. При этом натурным условиям с относительно малой начальной турбулентностью потока соответствует верхняя граница критических величин числа Рейнольдса Re* ≈ 3·105.
Аналогичный кризис обтекания при несколько бóльших критических числах Рейнольдса возникает и при обтекании кругового цилиндра. Из этого можно сделать вывод, что именно кризис обтекания приводит к сильной турбулизации дорожки вихрей Кармана за цилиндром при Re* ≈ 5·105. В новой конфигурации вихрей дорожка теряет устойчивость, и при Re ≥ 5·105 вместо нее образуется так называемый турбулентный спутный след. Как уже упоминалось, в отличие от тел с гладкими поверхностями на телах с разрывами гладкости поверхности (ребрами) вихри вне зависимости от значений числа Рейнольдса всегда сходят с этих ребер. Поэтому как для пластины, так и для тела, сечение которого изображено на рис. 7, точки схода вихрей всегда сохраняют свое неизменное положение, и зона определенных и устойчивых значений числа Струхаля вследствие этого должна быть распространена до значительно бóльших чисел Рейнольдса, возможно, вплоть до перекрытия со следующей зоной устойчивости, начинающейся где-то в окрестности Re ~ 107.
Из условия устойчивости дорожки вихрей, полученного в теории Кармана, следует, что существует единственное фиксированное отношение между поперечным h и продольным расстояниями L между вихрями [26]:
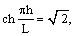(2)
откуда
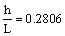
Для шахматного расположения цепочек, когда каждый вихрь верхней цепочки располагается точно посередине между ближайшими вихрями нижней цепочки, и наоборот (см. рис. 6, 7), скорости перемещения цепочек u относительно потока будут равны [26]
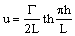(3)
При этом Γ – циркуляция этих вихрей.
Вихревая частота равна
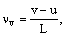(4)
а число Струхаля пропорционально частоте νv. Тогда, из формул (1) – (4) при заданной форме тела, а также скорости потока и циркуляции, следует, что
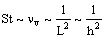(5)
Формула (5) объясняет увеличение числа Струхаля для дорожки Кармана, образующейся на круговом цилиндре, при Re > 5·106. В этом случае пограничный слой на поверхности тела становится полностью турбулентным, и, поэтому, точки его отрыва с поверхности, где зарождаются вихри, оказываются ближе к его продольной оси (параллельной вектору скорости набегающего потока), чем в ламинарном пограничном слое при 3·102 < Re < 3·105 [28]. Это приводит к тому, что и расстояние h между сторонами дорожки Кармана уменьшается, а ее число Струхаля растет от величины St ≈ 0.2 до величины St ≈ 0.3. Для этого достаточно уменьшения ширины дорожки на ~ 20 %.
Также становится понятным различие между числами Струхаля при обтекании кругового цилиндра и пластинки, поставленной поперек потока. Вихри срываются с ребер пластинки, но не с крайних поперечных точек поверхности кругового цилиндра, а с точек на его поверхности, которые расположены ближе к его продольной оси (см. рис. 6). Число Рейнольдса течения, показанного на этом рисунке, составляет Re = 140, тогда для цилиндра St ≈ 0.17 (см. рис. 8). Это означает, что при одинаковых поперечных размерах цилиндра и пластинки начальная, и, соответственно, установившаяся на некотором расстоянии от препятствия ширина дорожки вихрей за цилиндром должна быть процентов на 10 меньше, и число Струхаля, соответственно, – процентов на 20 выше (влияние различия скоростей на число Струхаля намного более слабое, и в данном случае им можно пренебречь). Можно видеть, что вертикальное удаление точек вихреобразования от продольной оси цилиндра на рис. 6 действительно примерно равно 90 % от его радиуса.
Рассмотрим теперь формирование дорожки Кармана на бесконечно длинном в продольном направлении теле с плоскими гранями, как если бы тело, изображенное на рис. 7 продолжалось вправо до бесконечности. Вихри всегда возникают на передних ребрах этого тела, при этом верхняя и нижняя стороны дорожки Кармана этим телом оказываются разделены, а сами вихри проходят вдоль его боковых твердых поверхностей. В невязкой сплошной среде граничное условие непротекания на твердой поверхности, как известно, может быть смоделировано с помощью отражения особенностей потока, то есть в рассматриваемом случае – вихрей [26]. Отражение вихрей должно производиться симметрично относительно этой твердой поверхности. Поэтому в математической модели, описывающей движение вихрей вдоль нее, появится цепочка фиктивных вихрей, которая вместе с реально существующей цепочкой в потоке образуют дорожку Кармана с симметричным расположением вихрей. И именно взаимодействие вихрей в каждой из этих двух новых дорожек Кармана определит их параметры.
Известно, что симметричное расположение вихрей является неустойчивым [26]. Это означает, что такие дорожки вихрей должны «рассыпаться» вскоре после своего образования, и, следовательно, число Струхаля для такого течения можно принять равным 0. Естественно предположить, что на реальных телах прямоугольного поперечного сечения числа Струхаля St будут иметь промежуточные величины между полученными выше крайними значениями St для пластинки и полубесконечного тела. Для их оценки можно использовать подходящую интерполяционную формулу, построенную по какому-либо набору экспериментальных данных, параметром которой должно быть отношение поперечной длины тела b к его высоте d:
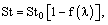(6)
где St0 – величина числа Струхаля для плоской пластинки, λ – удлинение тела b/d, f(λ) – функция, удовлетворяющая следующим условиям:
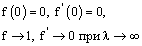(7)
Условие равенства 0 производной функции f при λ = 0 введено для того, чтобы при 0 ≤ λ ~ 1 число Струхаля слабо зависело от этого параметра (что соответствует экспериментальным данным), а при λ >> 1 – чтобы функция f(λ) асимптотически приближалась к 0. При 1 < λ ~ 10 эта функция должна давать значения, достаточно близкие к экспериментальным.
Исследование, описанное в статье про флаттер, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое флаттер, задача келдыша, бафтинг, эффект шимми , вобблинг и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Аэродинамика
Комментарии
Оставить комментарий
Аэродинамика
Термины: Аэродинамика