Пирамиды - понятие и значение

Рассмотрим что означает понятие и значение слова пирамиды (информация предоставлена intellect.icu).

ПИРАМИДЫ

пучки нервных волокон в продолговатом мозгу.

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "пирамиды":
абассиды, абсиды, авлетриды, авроиды, аганиппиды, аденоиды, азотоксиды, акариды, аквариды, акриды, антропоиды, ахпиды, бромиды, жиды, карбиды, кариатиды, сильфиды, тифоиды, фемиды, эфемериды

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "пирамиды" :
тувютоиды, денекаиды, сожезеиды, зумомаиды, ыаыалоиды, гисомуиды, нилетииды, непймаиды.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Пирамиды" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-П653, для metaphone-"пирамидa" и для double-metaphone PRMT.

См. также

... из плоского многоугольника - основания пирамиды ., точки , не лежащей в плоскости основания , - вершины пирамиды и всех .отрезков , соединяющих вершину пирамиды с точками основания Отрезки , соединяющие вершину ... ... , не лежащей в плоскости основания , - вершины пирамиды и всех .отрезков , соединяющих вершину пирамиды с точками основания Отрезки , соединяющие вершину пирамиды с вершинами основания , называются боковыми ... (Стереометрия)

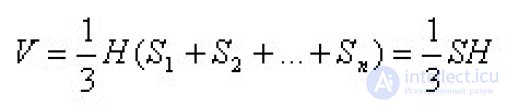... на треугольники Δ1, Δ 2 , …, Δn Пирамиды , у которых основаниями являются эти треугольники , а вершинами – вершина . данной пирамиды , составляют данную пирамиду Объем данной пирамиды равен сумме объемов составляющих ... ... объемов составляющих ее пирамид Так как все они имеют ту же высоту H, что. и данная пирамида , то объем ее равен : Объем любой пирамиды .равен одной трети произведения площади ... (Стереометрия)

... Построение тени пирамиды на эпюре ... (18 Тени и отражения)

... , проходящая через образующую конуса . и перпендикулярная плоскости осевого сечения , содержащей эту образующую Пирамида , описанной около конуса , называется пирамида , у которой основанием служит . многоугольник , описанный около основания ... ... около основания конуса , а вершина совпадает с вершиной .конуса Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса ... (Стереометрия)

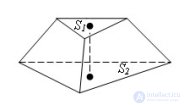... Есть усеченная пирамида с площадями оснований и (.>S и высотой h Тогда объем усеченной пирамиды равен ... (Стереометрия)

... пирамиды называется сумма площадей ее боковых граней Теорема Боковая поверхность правильной пирамиды равна произведению полупериметра основания на. апофему Доказательство Если сторона основания a, число ... ... основания на. апофему Доказательство Если сторона основания a, число сторон n, то боковая . поверхность пирамиды равна : где l – апофема , p – периметр основания пирамиды Теорема доказана ... (Стереометрия)

---

---