Создание рекомендательных систем: фильтрация содержимого и коллаборативная фильтрация.

Привет, Вы узнаете о том , что такое рекомендательная систем, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое рекомендательная систем, фильтрация содержимого, коллаборативная фильтрация , настоятельно рекомендую прочитать все из категории Экспертные системы.

В любой сфере, где пользователям предлагается контент в той или иной форме, рекомендации нового материала — важнейший элемент системы. Действительно, увеличение продаж даже на несколько процентов может принести миллионы долларов.

План :

1. Виды и области применения рекомендательных систем.
2. Простейшие алгоритмы.
3. Введение в линейную алгебру.
4. Алгоритм SVD.
5. Измерение качества рекомендаций.
6. Использование Matrix factorization для коллаборативной фильтрации
7. использование рекуррентных нейронных сетей
8. Направление развития.

Начнем с простого: что вообще такое рекомендательные системы, и какими они бывают. Наверное, все уже сталкивались с ними в интернете. Первый пример — рекомендательные системы фильмов.



На сайте imdb.com пользователи могут оценивать фильмы по десятибалльной шкале. Оценки агрегируются, получается средний рейтинг фильма. На этом же сайте есть блок с рекомендациями для конкретного пользователя. Если я зашел на сайт и оценил несколько фильмов, imdb сможет порекомендовать мне еще какие-нибудь фильмы. Похожий блок есть и на фейсбуке.

Нечто сходное, но только для музыки, делает last.fm. Он рекомендует мне исполнителей, альбомы, мероприятия, на которые мне стоит сходить. Сервис Pandora - персональное радио, которое постепенно подстраивается под пользователя на основе его оценок, и в итоге играет только те треки, которые ему нравятся.



Еще одна известная область — рекомендация товаров. На картинке ниже у нас, конечно же, Amazon. Если вы купили что-то на амазоне, за вами будут охотиться с дополнительными предложениями: похожими товарами или аксессуарами. Это хорошо и для пользователей (им не нужно искать эти товары самостоятельно), и конечно, это хорошо для самого магазина.



Мы перечислили три категории, но на самом деле их гораздо больше: заведения на карте, новости, статьи, сайты, концерты, театры, выставки, видео, книги, приложения, игры, путешествия, социальные связи и многое другое.

Виды рекомендательных систем

Можно выделить два основных типа рекомендательных систем. Их, конечно же больше, но мы сегодня будем рассматривать именно эти и в особенности коллаборативную фильтрацию.

1. Content-based ( фильтрация содержимого )
   • Пользователю рекомендуются объекты, похожие на те, которые этот пользователь уже употребил.
   • Похожести оцениваются по признакам содержимого объектов.
   • Сильная зависимость от предметной области, полезность рекомендаций ограничена.
2. коллаборативная фильтрация (Collaborative Filtering)
   • Для рекомендации используется история оценок как самого пользователя, так и других пользователей.
   • Более универсальный подход, часто дает лучший результат.
   • Есть свои проблемы (например, холодный старт).

Рекомендательные концепции возникли в сети интернет уже давно, приблизительно 20 лет назад. Но истинный рост в данной сфере произошел приблизительно 5-ДЕСЯТЬ лет назад, когда случилось соревнование Netflix Prize. Фирма Netflix в то время приносила в прокат никак не цифровые копии, а распространяла VHS-кассеты и DVD. С целью их существовало весьма немаловажно увеличить свойство советов. Нежели правильнее Netflix советует собственным юзерам кинофильмы, этим более кинофильмов они принимают в металлопрокат. В соответствии с этим, увеличивается и доход фирмы. В 2006 г. они бросили состязание Netflix Prize. Они сообщили в публичный допуск составленные сведения: приблизительно 100 млн. оценок согласно пятибалльной шкале с предписанием ID проставивших их юзеров. Члены состязания обязаны существовали равно как возможно правильнее предвидеть, тот или иной оценку установит конкретному кинофильму этот либо другой юзер. Свойство прогноза измерялось присутствие поддержки метрики RMSE (средне-квадратное отклонение). У Netflix ранее был метод, какой предрекал балла юзеров с качеством 0.9514 согласно метрике RMSE. Цель существовала усовершенствовать предвидение несмотря на то б в 10% — вплоть до 0.8563. Победителю был сулен награда в $ 1 000 000. Состязание продолжалось приблизительно 3 годы. Из-за 1-ый время свойство повысили в 7%, далее все-таки несколько замедлилось.

Но в конце две команды прислали свои решения, каждое из которых проходило порог в 10%, качество у них было одинаковое с точностью до четвертого знака. В задаче, над которой множество команд билось три года, все решили каких-то двадцать минут. Опоздавшая команда (как и многие другие, участвовавшие в конкурсе) остались ни с чем, однако сам конкурс очень сильно подстегнул развитие в этой области.

Простейшие алгоритмы

Для начала формализуем нашу задачу. Что мы имеем? У нас есть множество пользователей

&#119906 в€€ &#119880, множество объектов &#119894 в€€ &#119868 (фильмы, треки, товары и т.п.) и множество событий (&#119903_{&#119906&#119894}, &#119906, &#119894, ...) в€€ &#119967 (действия, которые пользователи совершают с объектами). Каждое событие задается пользователем &#119906, объектом &#119894, своим результатом &#119903_{&#119906&#119894} и, возможно, еще какими-то характеристиками. От нас требуется:

• предсказать предпочтение:
  
  &#119903&#770_{&#119906&#119894} = Predict (&#119906,&#119894,...) ≈ &#119903_{&#119906&#119894}.
• персональные рекомендации:
  
  &#119906 &#10236 (&#119894₁,...,&#119894_&#120338) = Recommend_&#120338(&#119906,...).
• похожие объекты:
  
  &#119906 &#10236 (&#119894₁,...,&#119894_&#119872) = Similar_&#119872(&#119894).

Таблица оценок


Допустим, нам дана таблица с оценками пользователей:







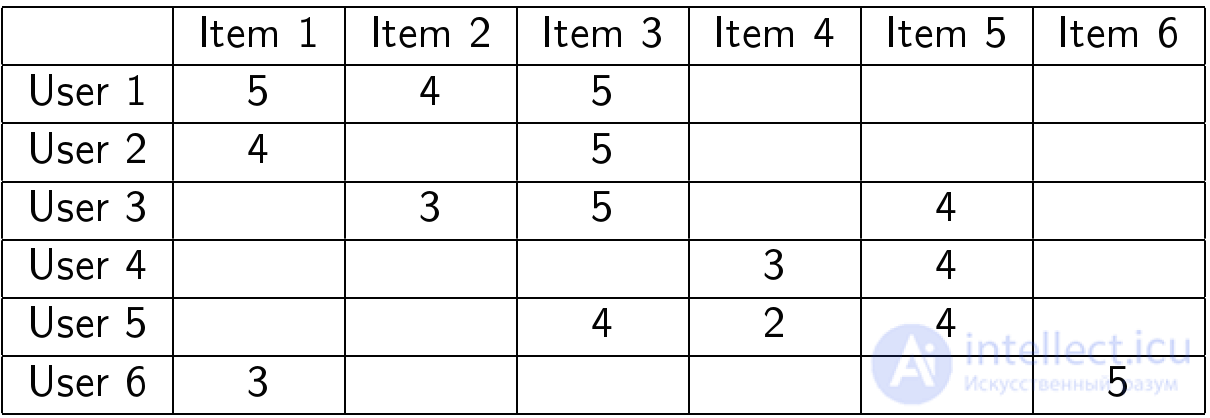
На нужно как можно лучше предсказать, какие оценки должны быть в ячейках со знаками вопроса:








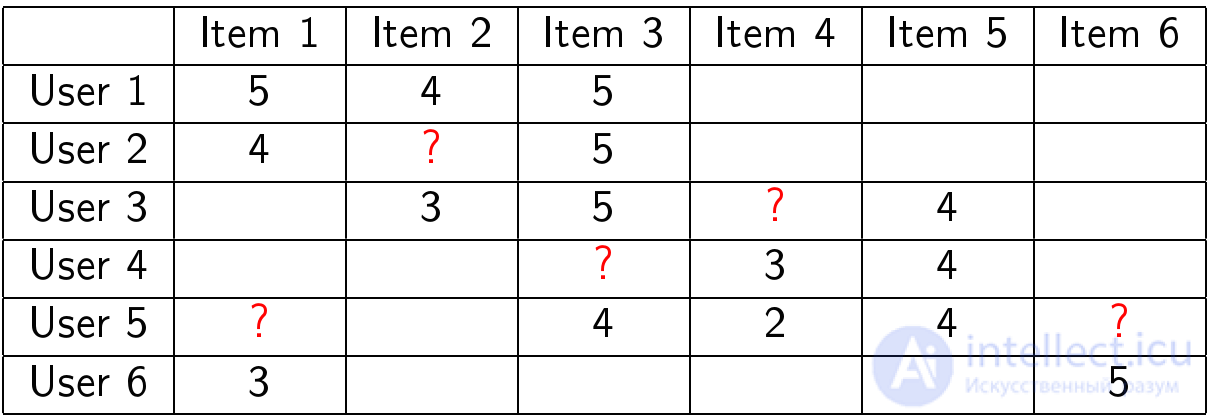
Кластеризация пользователей


Напомним, что основная идея коллаборативной фильтрации — похожим пользователям обычно нравятся похожие объекты. Начнем с самого простого метода.

• Выберем некоторую условную меру схожести пользователей по их истории оценок &#119904&#119894&#119898(&#119906, &#119907).
• Объединим пользователей в группы (кластеры) так, чтобы похожие пользователи оказывались в одном кластере: &#119906 &#10236 &#119865(&#119906).
• Оценку пользователя объекту будем предсказывать как среднюю оценку кластера этому объекту:

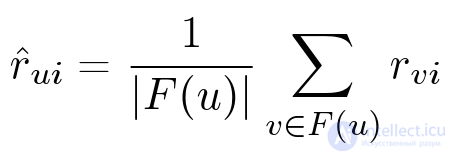
У этого алгоритма есть несколько проблем:

• Нечего рекомендовать новым/нетипичным пользователям. Для таких пользователей не найдется подходящего кластера с похожими на них пользователями.
• Не учитывается специфика каждого пользователя. В каком-то смысле мы делим всех пользователей на какие-то классы (шаблоны).
• Если в кластере никто не оценивал объект, то предсказание сделать не получится.

User-based


Попробуем несколько улучшить предыдущий метод и заменить жесткую кластеризацию на следующую формулу:

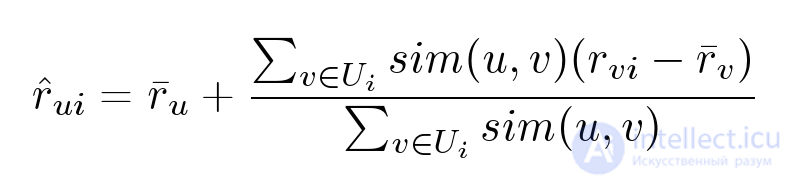
Однако у этого алгоритма также есть свои проблемы:

• Нечего рекомендовать новым/нетипичным пользователям. Для таких пользователей мы все еще не можем найти похожих.
• Холодный старт — новые объекты никому не рекомендуются.

Item-based


Есть абсолютно симметричный алгоритм:

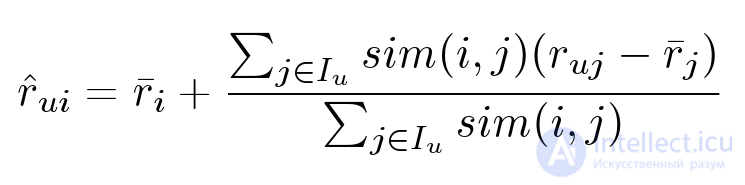
В предыдущем методе мы отталкивались от идеи, что, скажем, фильм понравится пользователю, если он понравился его друзьям. Об этом говорит сайт https://intellect.icu . Здесь же мы считаем, что фильм понравится пользователю, если ему понравились похожие фильмы.



Проблемы:

• Холодный старт — новые объекты никому не рекомендуются.
• Рекомендации часто тривиальны.

Общие проблемы перечисленных методов


Все перечисленные методы обладают следующими недостатками:

• Проблема холодного старта.
• Плохие предсказания для новых/нетипичных пользователей/объектов.
• Тривиальность рекомендаций.
• Ресурсоемкость вычислений. Для того, чтобы делать предсказания нам нужно держать в памяти все оценки всех пользователей.

Поэтому перейдем к более сложному алгоритму, который практически лишен этих недостатков.




Алгоритм SVD


Для этого алгоритма нам потребуется несколько понятий из линейной алгебры: векторы, матрицы и операции с ними. Я не буду здесь приводить все определения, если вам нужно освежить эти знания, то все объяснения есть в видеозаписи лекции примерно с 33 минуты.



SVD (Single Value Decomposition), переводится как сингулярное разложение матрицы. В теореме о сингулярном разложении утверждается, что у любой матрицы &#119808 размера &#119899Г—&#119898 существует разложение в произведение трех матриц: &#119880, &#425 &#1080 &#119881^&#119879:

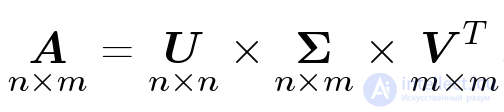
Матрицы &#119880 и &#119881 ортогональные, а &#425 — диагональная (хотя и не квадратная).

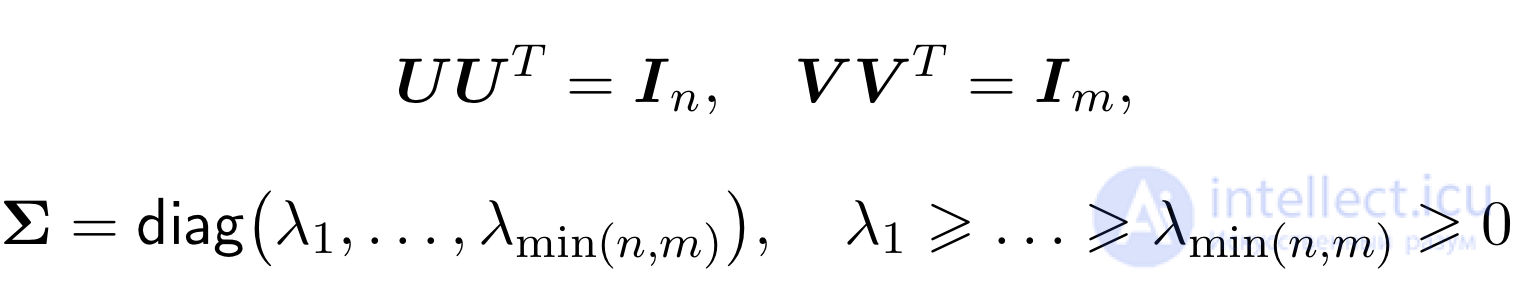
Причем лямбды в матрице &#425 будут упорядочены по невозрастанию. Сейчас мы эту теорему не будем доказывать не будем, просто воспользуемся самим разложением.



Но что нам с того, что мы можем какую-то матрицу в произведение трех еще более непонятных матриц. Для нас тут будет интересно следующее. Помимо обычного разложения бывает еще усеченное, когда из лямбд, остаются только первые &#119889 чисел, а остальные мы полагаем равными нулю.

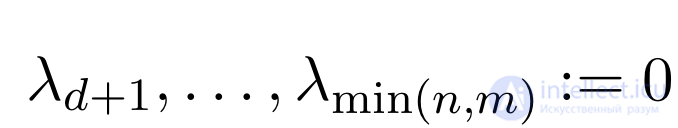
Это равносильно тому, что у матриц &#119880 и &#119881 мы оставляем только первые &#119889

столбцов, а матрицу &#425 обрезаем до квадратной &#119889Г—&#119889.

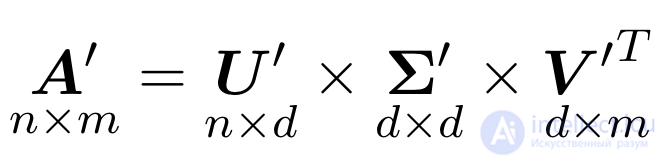
Так вот, оказывается, что полученная матрица &#119808′ хорошо приближает исходную матрицу &#119808 и, более того, является наилучшим низкоранговым приближением с точки зрения средне-квадратичного отклонения.




SVD для рекомендаций


Как же использовать все это для рекомендаций? У нас была матрица, мы разложили ее в произведение трех матриц. При чем разложили не точно, а приблизительно. Упростим все немного, обозначив произведение первых двух матриц за одну матрицу:

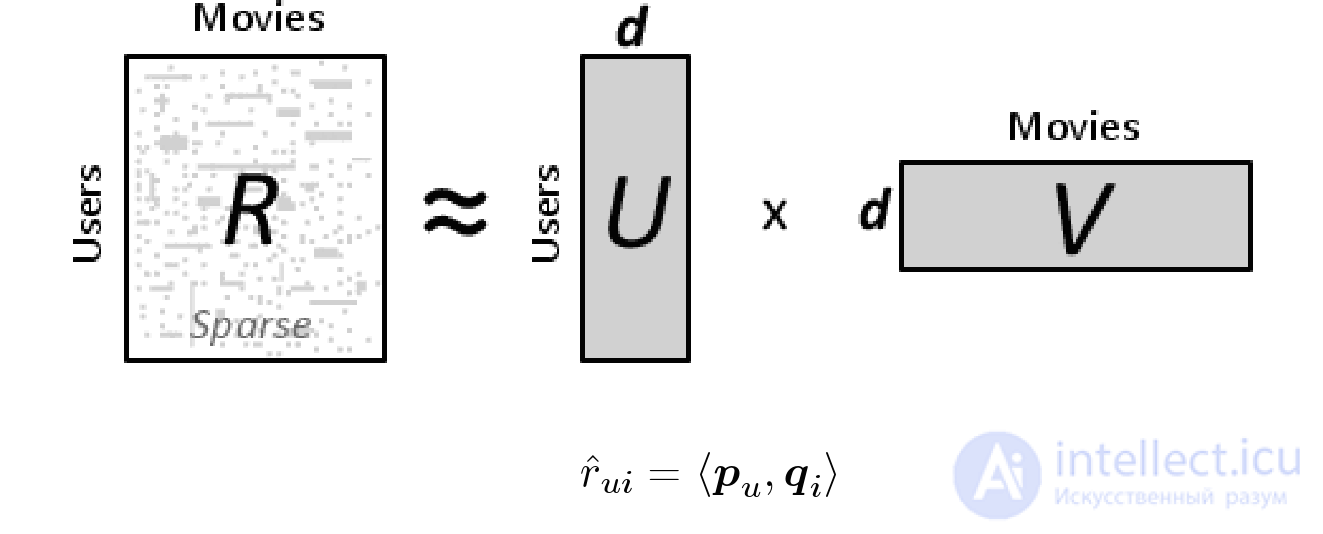
Теперь отвлечемся немного от всех этих матриц и сконцентрируемся на получившемся алгоритме: чтобы предсказать оценку пользователя &#119880 для фильма &#119868, мы берем некоторый вектор &#119901_&#119906 (набор параметров) для данного пользователя и вектор для данного фильма &#119902_&#119894. Их скалярное произведение и будет нужным нам предсказанием: &#119903&#770_{&#119906&#119894} = &#10216&#119901_&#119906,&#119902_&#119894&#10217.



Алгоритм достаточно простой, но дает удивительные результаты. Он не просто позволяет нам предсказывать оценки. С его помощью мы можем по истории пользователей выявлять скрытые признаки объектов и интересы пользователей. Например, может так получиться, что на первой координате вектора у каждого пользователя будет стоять число, показывающее, похож ли пользователь больше на мальчика или на девочку, на второй координате — число, отражающее примерный возраст пользователя. У фильма же первая координата будет показывать, интересен ли он больше мальчикам или девочкам, а вторая — какой возрастной группе пользователей он интересен.



Но не все так просто. Есть несколько проблем. Во-первых, матрица оценок &#119929 нам полностью не известна, поэтому мы не можем просто взять ее SVD-разложение. Во-вторых, SVD-разложение не единственное: (&#119880О©)&#425(&#119881О©)_&#119879=&#119880&#425&#119881_&#119879, поэтому даже если мы найдем хоть какое-то разложение, вряд ли именно в нем первая координата будет соответствовать полу пользователя, а вторая — возрасту.




Обучение


Попробуем разобраться с первой проблемой. Тут нам понадобится машинное обучение. Итак, мы не можем найти SVD-разложение матрицы, т.к. мы не знаем саму матрицу. Но мы хотим воспользоваться этой идеей и придумать модель предсказания, которая будет работать сходным с SVD образом. Наша модель будет зависеть от многих параметров — векторов пользователей и фильмов. Для заданных параметров, чтобы предсказать оценку, мы возьмем вектор пользователя, вектор фильма и получим их скалярное произведение:

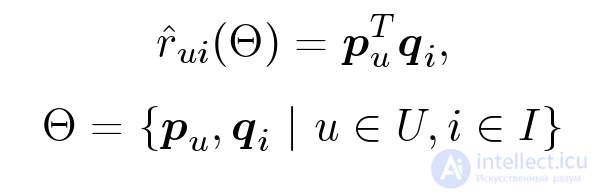
Но так как векторов мы не знаем, их еще нужно получить. Идея заключается в том, что у нас есть оценки пользователей, при помощи которых мы можем найти такие оптимальные параметры, при которых наша модель предсказывала бы эти оценки как можно лучше:

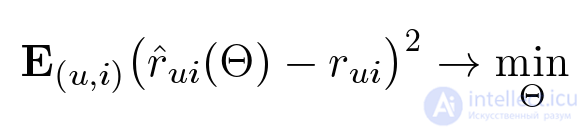
Итак, мы хотим найти такие параметры Ое, чтобы квадрат ошибки был как можно меньше. Но тут есть парадокс: мы хотим меньше ошибаться в будущем, но мы не знаем, какие оценки у нас будут спрашивать. Соответственно и оптимизировать это мы не можем. Но нам известны уже проставленные пользователями оценки. Попробуем подобрать параметры так, чтобы на тех оценках, которые у нас уже есть, ошибка была как можно меньше. Кроме того, добавим еще одно слагаемое — регуляризатор.

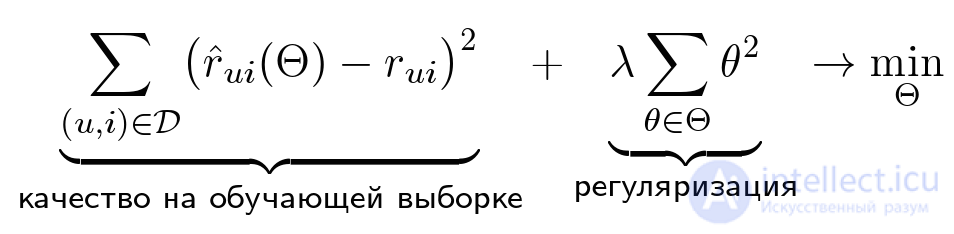
Зачем нужен регуляризатор?


Регуляризация нужна для борьбы с переобучением — явлением, когда построенная модель хорошо объясняет примеры из обучающей выборки, но достаточно плохо работает на примерах, не участвовавших в обучении. Вообще, методов борьбы с переобучением существует несколько, хочется отметить два из них. Во-первых, нужно выбирать простые модели. Чем проще модель, тем лучше она обобщается на будущие данные (это похоже на известный принцип бритвы Оккама). А второй метод — это как раз регуляризация. Когда мы настраиваем модель для обучающей выборки, мы оптимизируем ошибку. Регуляризация заключается том, что мы оптимизируем не просто ошибку, а ошибку плюс некоторая функция от параметров (например, норма вектора параметров). Это позволяет ограничить размер параметров в решении, уменьшает степень свободы модели.




Численная оптимизация


Как же нам найти оптимальные параметры? Нам нужно оптимизировать вот такой функционал:

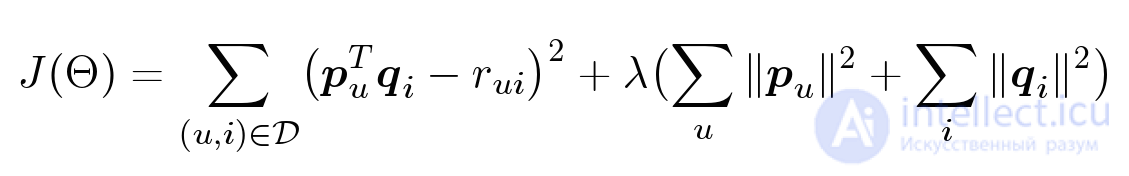
Параметров много: для каждого пользователя, для каждого объекта у нас есть свой вектор, который мы хотим оптимизировать. У нас есть функция, зависящая от большого количества переменных. Как найти ее минимум? Тут нам потребуется градиент — вектор из частных производных по каждому параметру.

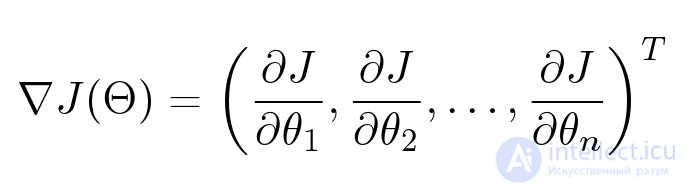
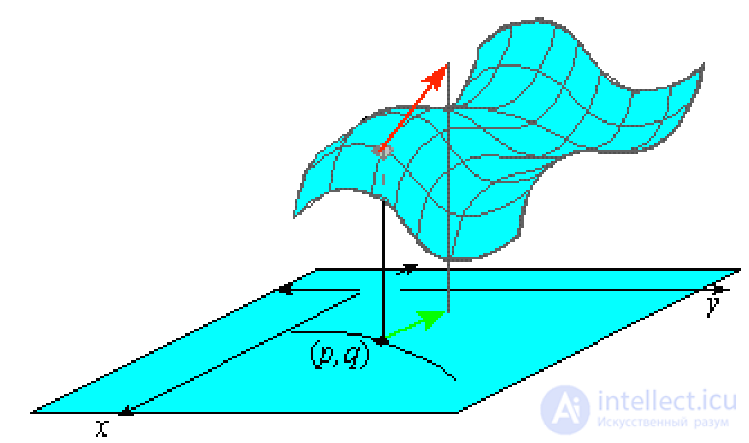
Градиент очень удобно представлять себе визуально. На иллюстрации у нас изображена поверхность: функция от двух переменных. Например, высота над уровнем моря. Тогда градиент в какой-нибудь конкретной точке — это такой вектор, направленный в ту сторону, куда больше всего растет наша функция. А если пустить воду из этой точки, она потечет по направлению противоположному градиенту.

Самый известный метод оптимизации функций — градиентный спуск. Допустим у нас есть функция от многих переменных, мы хотим ее оптимизировать. Мы берем какое-нибудь изначальное значение, а потом смотрим, куда можно двигаться, чтобы минимизировать это значение. Метод градиентного спуска — это итеративный алгоритм: он многократно берет параметры определенной точки, смотрит на градиент и шагает против его направления:

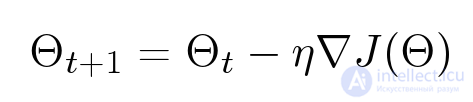
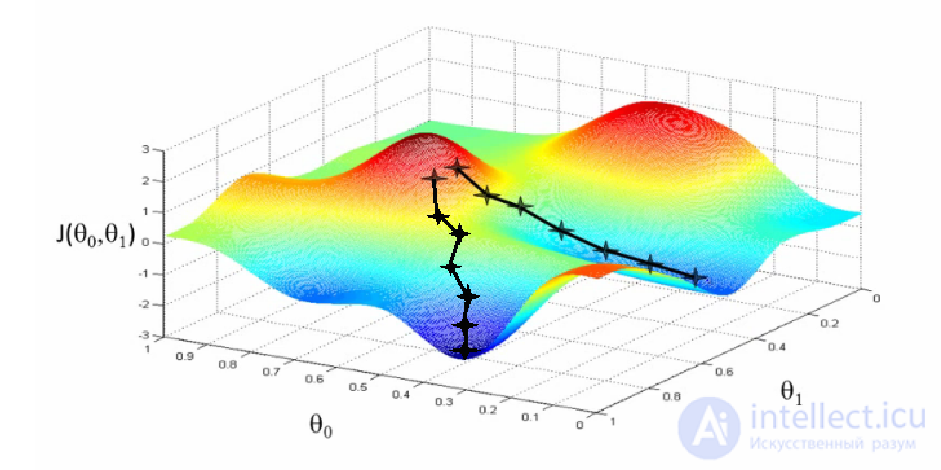
Проблемы этого метода заключаются в том, что он, во-первых, в нашем случае работает очень медленно и, во-вторых, находит локальные, а не глобальные минимумы. Вторая проблема для нас не так страшна, т.к. в нашем случае значение функционала в локальных минимумах оказывается близким к глобальному оптимуму.




Altering Least Squares


Однако метод градиентного спуска применять нужно не всегда. Например, если нам нужно посчитать минимум для параболы, действовать этим методом необходимости нет, мы точно знаем, где находится ее минимум. Оказывается, что функционал, который мы пытаемся оптимизировать — сумма квадратов ошибок плюс сумма квадратов всех параметров — это тоже квадратичный функционал, он очень похож на параболу. Для каждого конкретного параметра, если мы зафиксируем все остальные, это будет как раз параболой. Т.е. минимум по одной координате мы можем точно определить. На этом соображении и основан метод Altering Least Squares. Я не буду на нем подробно останавливаться. Скажу лишь, что в нем мы попеременно точно находим минимумы то по одним координатам, то по другим:

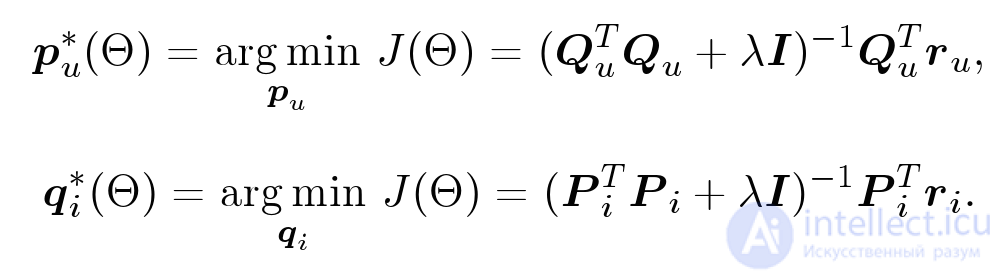
Мы фиксируем все параметры объектов, оптимизируем точно параметры пользователей, дальше фиксируем параметры пользователей и оптимизируем параметры объектов. Действуем итеративно:

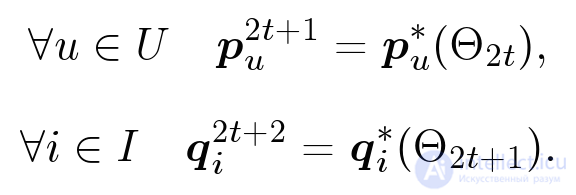
Работает все это достаточно быстро, при этом каждый шаг можно распараллелить.




Измерение качества рекомендаций


Если мы хотим улучшить качество рекомендаций, нам нужно научиться его измерять. Для этого алгоритм, обученный на одной выборке — обучающей, проверяется на другой — тестовой. Netflix предложил измерять качество рекомендаций по метрике RMSE:

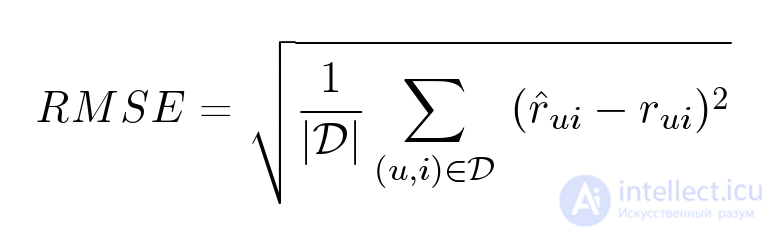
Сегодня это стандартная метрика для предсказания оценки. Однако у нее есть свои недостатки:

• У каждого пользователя свое представление о шкале оценок. Пользователи, у которых разброс оценок более широкий, будут больше влиять на значение метрики, чем другие.
• Ошибка в предсказании высокой оценки имеет такой же вес, что и ошибка в предсказании низкой оценки. При этом предсказать оценку 9 вместо настоящей оценки 7 страшнее, чем предсказать 4 вместо 2 (по десятибалльной шкале).
• Можно иметь почти идеальную метрику RMSE, но иметь очень плохое качество ранжирования, и наоборот.

Метрики ранжирования


Существуют и другие метрики — метрики ранжирования, например, основанные на полноте и точности. Пусть &#119929 — множество рекомендованных объектов, &#119927 — множество объектов, которые на самом деле пользователю понравятся.

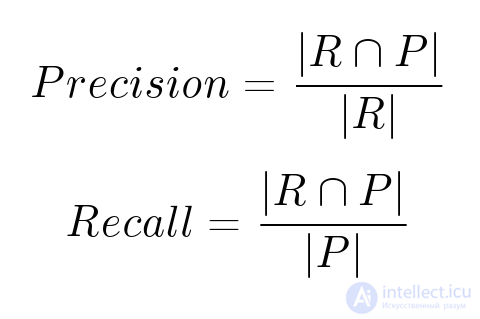
Тут тоже есть проблемы:

• Нет данных про рекомендованные объекты, которые пользователь не оценивал.
• Оптимизировать эти метрики напрямую почти невозможно.

Другие свойства рекомендаций


Оказывается, что на восприятие рекомендаций влияет не только качество ранжирования, но и некоторые другие характеристики. Среди них, например, разнообразие (не стоит выдавать пользователю фильмы только на одну тему или из одной серии), неожиданность (если рекомендовать очень популярные фильмы, то такие рекомендации будут слишком банальными и почти бесполезными), новизна (многим нравятся классические фильмы, но рекомендациями обычно пользуются, чтобы открыть для себя что-то новое) и многие другие.




Похожие объекты


Похожесть объектов не такая уж очевидная вещь. К этой задаче могут быть разные подходы:

• Похожие объекты — это объекты, похожие по своим признакам (content-based).
• Похожие объекты — это объекты, которые часто используют вместе («клиенты, купившие &#119894, также покупали &#119895»).
• Похожие объекты — это рекомендации пользователю, которому понравился данный объект.
• Похожие объекты — это просто рекомендации, в которых данный объект выступает в качестве контекста.

Направления развития



Концептуальные вопросы

• Как строить списки рекомендаций на основе предсказаний? (Обычный топ — не всегда лучшая идея.)
• Как улучшать качество именно рекомендаций, а не предсказаний?
• Как измерять похожести объектов?
• Как обосновывать рекомендации? (Оказывается, пользователи намного лучше воспринимают рекомендации, если снабжать их какими-то объяснениями.)

Технические вопросы

• Как решать проблему холодного старта для новых пользователей и новых объектов?
• Как быстро обновлять рекомендации? (От этого может сильно зависеть польза введения рекомендаций в ваш сервис.)
• Как быстро находить объекты с наибольшим предсказанием?
• Как измерять качество онлайн-рекомендаций? (Традиционный подход с обучающей и тестовой выборками может работать не очень хорошо.)
• Как масштабировать систему?

Как учитывать дополнительную информацию?

• Как учитывать не только явный (explicit), но и неявный (implicit) фидбек? (Неявного фидбека часто бывает на порядки больше.)
• Как учитывать контекст? (Context-aware recommendations)
• Как учитывать признаки объектов? (Гибридные системы)
• Как учитывать связи между объектами? (таксономию)
• Как учитывать признаки и связи пользователей?
• Как учитывать информацию из других источников и предметных областей? (Cross-domain recommendations)

Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области рекомендательная систем имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое рекомендательная систем, фильтрация содержимого, коллаборативная фильтрация и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Экспертные системы

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.