Лекция
Привет, Вы узнаете о том , что такое алгоритм прима онлайн, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритм прима онлайн, минимальное остовное дерево, алгоритм прима, prim algorithm, остовное дерево, максимальное остовное дерево , настоятельно рекомендую прочитать все из категории Классические алгоритмы онлайн.
.
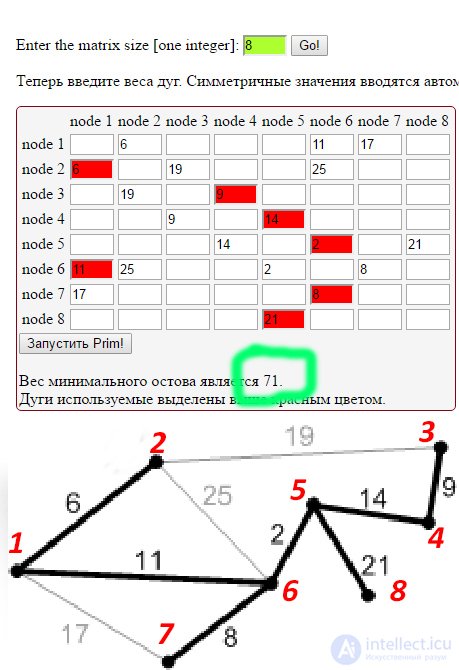
Алгоритм Прима принимает квадратную матрицу (представляющую собой граф с взвешенными дугами) и находит дуги, которые образуют минимального остов . .
1. введите размерность матрицы
2. заполните матрицу инцидентности для вашего графа
3. нажмите "запустить Prim"
4. выделите на вашем графе нужные дуги входящие в остновное дерево, проверьте общий вес
пример расчета и преобразования графа в матрицу на картинке ниже
Задача построения минимального остовного дерева встречается в различных областях. Интересным ее применением является проблема построения смешанного остовного дерева (Dana Richards and Jeffrey S. Salowe. Mixed spanning trees in theory and practice. International Journal Of Computational Geometry & Applications. Vol. 9, No. 3 (1999), 277-292): построить для графа дерево со свойствами минимального остовного дерева и дерева кратчайших путей. Другой важной задачей является быстрое обновление минимального остовного дерева при изменении графа. В статьеSajal K. Das, Paolo Ferragina "An Erew Pram algorithm for updating minimum spanning trees" показано, как для графа с n вершинами и m ребрами выполнить обновление одного ребра за учетное время O(logn).
Проблема построения минимального остовного дерева достаточно разносторонняя, и продолжает исследоваться и сегодня. В настоящей статье представлены только базовые алгоритмы. Ознакомиться с более продвинутыми алгоритмами можно по статьям из списка используемой литературы.
Алгоритм Крускала объединяет вершины графа в несколько связных компонент, каждая из которых является деревом. На каждом шаге из всех ребер, соединяющих вершины из различных компонент связности, выбирается ребро с наименьшим весом. Необходимо проверить, что оно является безопасным. Безопасность ребра гарантируется ранее доказанной теоремой о безопасных ребрах. Так как ребро является самым легким из всех ребер, выходящих из данной компоненты, оно будет безопасным.
Остается понять, как реализовать выбор безопасного ребра на каждом шаге. Для этого в алгоритме Крускала все ребра графа G перебираются по возрастанию веса. Для очередного ребра проверяется, не лежат ли концы ребра в разных компонентах связности, и если это так, ребро добавляется, и компоненты объединяются.
Удобно использовать для хранения компонент структуры данных для непересекающихся множеств, как, например, списки или, что лучше, лес непересекающихся множеств со сжатием путей и объединением по рангу (один из самых быстрых известных методов). Элементами множеств являются вершины графа, каждое множество содержит вершины одной связной компоненты. Для работы с множествами используются следующие процедуры:
| Make-Set(v) | Создание множества из набора вершин |
| Find-Set(v) | Возвращает множество, содержащее данную вершину |
| Union(u,v) | Объединяет множества, содержащие данные вершины |
Общая схема алгоритма выглядит так:
MST-KRUSKAL(G,w)
1: A ← 0
2: foreach (для каждой) вершины v ∈ V[G]
3: do Make-Set(v)
4: упорядочить ребра по весам
5: for (u,v) ∈ E (в порядке возрастания веса)
6: do if Find-Set(u) ≠ Find-Set(v) then
7: A ← A ∪ {(u,v)}
8: Union(u,v)
9: return A
На рисунках К1-К8 представлена работа алгоритма.
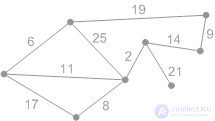 Рис. К1. Начальная фаза. Минимальный покрывающий лес пуст. |
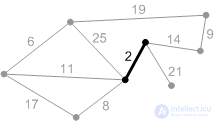 Рис. К2. Перебираем ребра в порядке возрастания веса: первое ребро с весом 2. Добавляем его к А. |
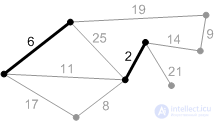 Рис. К3. Следующее безопасное ребро с весом 6. Добавляем его. |
 Рис. К4. |
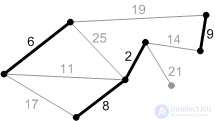 Рис. К5. |
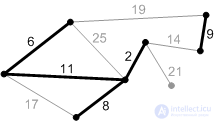 Рис. К6. |
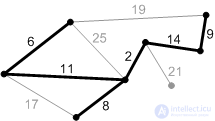 Рис. Об этом говорит сайт https://intellect.icu . К7. |
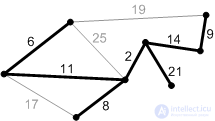 Рис. К8. Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено. |
Подсчитаем время работы алгоритма. Будем считать, что для хранения непересекающихся множеств используется метод с объединением по рангу и сжатием путей ( , 21.3), т.к. это самый быстрый способ из известных на сегодняшний день. Инициализация занимает время O(V), упорядочение ребер в строке 4 – O(ElogE). Далее производится O(E) операций, в совокупности занимающих время O(Eα’(E,V)), где α’ - функция, обратная к функции Аккермана (см. , 21.4). Поскольку α’(E,V) = o(logE), общее время работы алгоритма Крускала составляет O(ElogE) (основное время уходит на сортировку).
Как и алгоритм Крускала, алгоритм Прима следует общей схеме алгоритма построения минимального остовного дерева: на каждом шаге мы добавляем к строящемуся остову безопасное ребро. Алгоритм Прима относится к группе алгоритмов наращивания минимального остова: на каждом шаге существует не более одной нетривиальной (не состоящей из одной вершины) компоненты связности, и каждый к ней добавляется ребро наименьшего веса, соединяющее вершины компоненты с остальными вершинами. По теореме такое ребро является безопасным.
При реализации надо уметь на каждом шаге быстро выбирать безопасное ребро. Для этого удобно воспользоваться очередью с приоритетами (кучей). Алгоритм получает на вход граф G и его корень r – вершина, на которой будет наращиваться минимальный остов. Все вершины G, еще не попавшие в дерево, хранятся в очереди с приоритетом Ω. Приоритет вершины v определяется значением key[v], которое равно минимальному весу ребер, соединяющих v с вершинами минимального остова. Поле p[v] для вершин дерева указывает на родителя, а для вершин из очереди, указывает на ноду дерева, в которою ведет ребро с весом key[v] (одно из таких ребер, если их несколько).
Тогда алгоритм Прима выглядит следующим образом:
MST-PRIM(G,w, r)
1: Ω ← V[G]
2: foreach (для каждой) вершины u ∈ Ω
3: do key[u] ← ∞
4: key[r] ← 0
5: p[r] = NIL
6: while (пока) Ω ≠ 0
7: do u ← EXTRACT-MIN(Ω)
8: foreach (для каждой) вершины v ∈ Adj(u)
9: do if v ∈ Ω и w(u,v) < key[v] then
10: p[v] ← u
11: key[v] ← w(u,v)
На рисунках П1-П8 показана схема работы алгоритма Прима с корнем r.
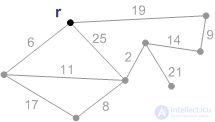 Рис. П1. Начальная фаза. Минимальный покрывающий лес состоит из корня и пустого множества ребер. |
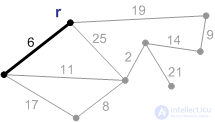 Рис. П2. Ребро с весом 6 является минимальным ребром, соединяющим корень с остальными вершинами. Добавляем его к минимальному остову. |
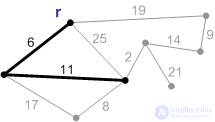 Рис. П3. Следующее безопасное ребро с весом 11. Добавляем его. |
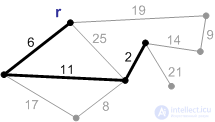 Рис. П4. |
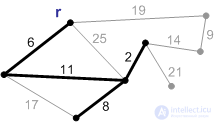 Рис. П5. |
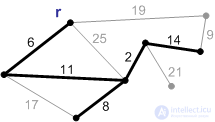 Рис. П6. |
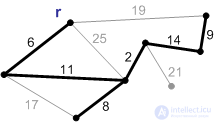 Рис. П7. |
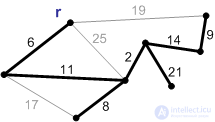 Рис. П8. Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено. |
Время работы алгоритма Прима зависит от того, как реализована очередь с приоритетами Ω. Если использовать двоичную кучу, инициализацию в строках 1-4 можно выполнить за время O(V). Далее цикл выполняется |V| раз, и каждая операция EXTRACT-MIN занимает время O(VlogV). Цикл for в строках 8-11 выполняется в общей сложности O(E), поскольку сумма степеней вершин графа равна 2|E|. Проверку принадлежности в строке 9 можно выполнить за время O(1), если хранить состояние очереди еще и как битовый вектор размера |V|. Присваивание в строке 11 подразумевает выполнение операции уменьшения ключа (DECREASE-KEY), которая для двоичной кучи может быть выполнена за время O(logV). Таким образом всего получаем O(VlogV+ElogV)=O(ElogV).
Лучшую оценку можно получить, если использовать фибоначчиевы кучи. С помощью фибоначчиевых куч можно выполнить операцию EXTRACT-MIN за учетное время O(logV), а операциюDECREASE-KEY – за учетное время O(1). В этом случае суммарное время работы алгоритма Прима составит O(E+VlogV).
Хотя оба алгоритма работают за (O(M log N)), существуют константные различия в скорости их работы. На разреженных графах (количество ребер примерно равно количеству вершин) быстрее работает алгоритм Крускала, а на насыщенных (количество ребер примерно равно квадрату количеству вершин) - алгоритм Прима (при использовании матрицы смежности).
На практике чаще используется алгоритм Крускала.
противоположность алгоритму Крускала для минимального остовного дерева - является нахождение максимального остовного дерева.
Один из методов вычисления максимального веса остовного дерева сети G – благодаря Крускалу-можно резюмировать следующим образом.
- Отсортируйте ребра G в порядке убывания по весу. Пусть t-множество ребер, образующих остовное дерево максимального веса. Установите T = ∅.
- Добавьте первое ребро к т.
- Добавьте следующее ребро к T тогда и только тогда, когда оно не образует цикл в T. Если оставшихся ребер нет, выйдите и сообщите, что G отключен.
- Если T имеет n-1 ребер (где n-число вершин в G), остановитесь и выведите T . В противном случае перейдите к шагу 3.
"Максимальное связующее дерево - это связующее дерево взвешенного графа, имеющего максимальный вес. Он может быть вычислен путем отрицания весов для каждого ребра и применения алгоритма Крускала (Pemmaraju and Skiena, 2003, p. 336)."
Если вы инвертируете вес на каждом ребре и минимизируете его, получите ли вы максимальное связующее дерево? Если это сработает, вы можете использовать тот же алгоритм. Конечно, нулевой вес будет проблемой.
Таким образом, мы получим максимальное связующее дерево.
Это дерево удовлетворяет любому ребру вне дерева, если оно добавлено, то образует цикл, а ребро вне <=-любые веса ребер в цикле
На самом деле это необходимое и достаточное условие для того, чтобы связующее дерево было максимальным связующим деревом.
ПФ.
Необходимо: очевидно, что это необходимо, или мы могли бы поменять ребро местами, чтобы сделать дерево с большей суммой Весов ребер.
Достаточно: предположим, что дерево T1 удовлетворяет этому условию, а T2-максимальное связующее дерево.
Тогда для ребер T1 ∪ T2 существуют только ребра T1, только ребра T2, только ребра T1 ∩ T2, если мы добавим к T2 только ребро T1(x1, xk), мы знаем, что оно образует цикл, и мы утверждаем, что в этом цикле должно существовать одно только ребро T2, которое имеет те же веса ребер, что и (x1, xk). Затем мы можем обменять эти ребра, чтобы получить дерево с еще одним ребром, общим с T2, и иметь ту же сумму весов ребер, повторяя это, мы получим T2. таким образом, T1 также является максимальным остовным деревом.
Докажите это утверждение:
предположим, что это не так, в цикле мы должны иметь только ребро T2, так как T1-это дерево. Если ни одно из T2-только ребер не имеет значения, равного значению (x1, xk), то каждое из T2-только ребер делает петлю с деревом T1, тогда T1 имеет петлю, приводящую к противоречию.
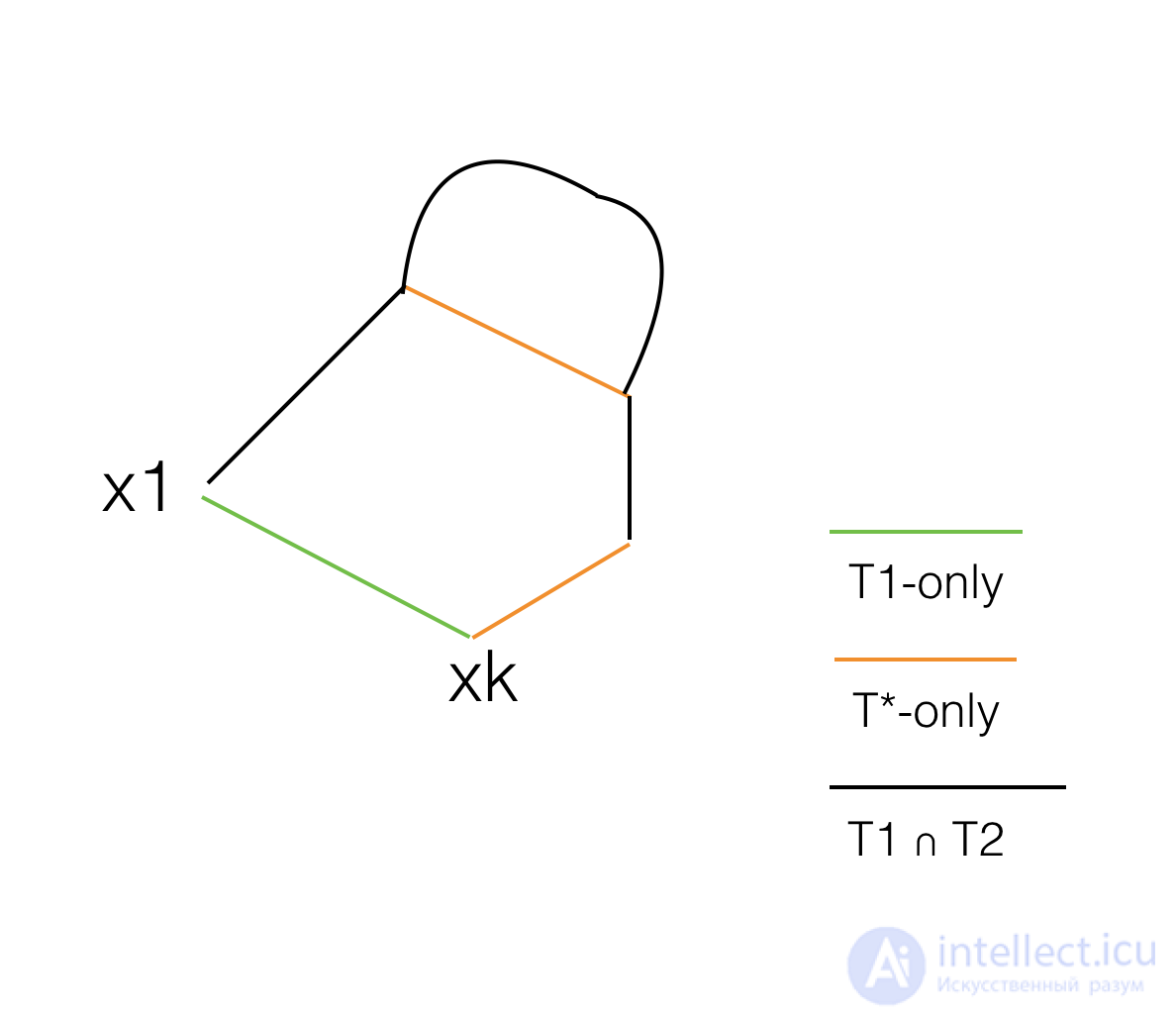
Этот алгоритм взят у UTD профессора R. Примечания цхандрасекаран по. Вы можете обратиться сюда: Single Commodity Multi-terminal Flows.
есть другой подход для нахождения максимального остовного дерева (MST) в графе G=(V, E)
Мы можем применить какой-то алгоритм Прима для нахождения MST. Для этого я должен определить свойство Cut для максимального взвешенного ребра.
Свойство Cut: допустим, в любой точке у нас есть множество S, которое содержит вершины, находящиеся в MST( пока предположим, что оно вычисляется каким-то образом ). Теперь рассмотрим множество S/V ( вершины не в MST ):
Утверждение: ребро от S до S/V, имеющее максимальный вес, всегда будет находиться в каждом MST.
Доказательство: предположим,что в точке, когда мы добавляем вершины в наше множество S, максимальное взвешенное ребро от S до S/V равно e=(u, v), где u находится в S, а v-в S/V.. Добавьте ребро e к MST. Это создаст цикл в исходном MST. Пересеките цикл и найдите вершины u' в S и v' в S/V такие, что u' - последняя вершина в S, после которой мы входим в S / V, а v' - первая вершина в S/V на пути в цикле от u до v.
Удалите ребро e'=(u', v'), и результирующий граф все еще связан, но вес e больше, чем e' [ так как e является максимальным взвешенным ребром от S до S/V в этой точке], так что это приводит к MST, который имеет сумму весов больше, чем исходный MST. Так что это противоречие. Это означает, что ребро e должно быть в каждом MST.
Алгоритм поиска MST:
Start from S={s} //s is the start vertex while S does not contain all vertices do { for each vertex s in S add a vertex v from S/V such that weight of edge e=(s,v) is maximum } end while
Реализация: мы можем реализовать с помощью Max Heap / Priority Queue, где ключ - это максимальный вес ребра от вершины в S до вершины в S/V, а значение-сама вершина. Добавление вершины в S равно Extract_Max из кучи, и при каждом Extract_Max изменяется ключ вершин, соседних с только что добавленной вершиной.
Таким образом, требуется m операций Change_Key и n операций Extract_Max.
Extract_Min и Change_Key как можно реализовать за o(зарегистрируйте N). n - число вершин.
Таким образом, это занимает O(m log n) времени. m - это число ребер в графе.
Выводы из данной статьи про алгоритм прима онлайн указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое алгоритм прима онлайн, минимальное остовное дерево, алгоритм прима, prim algorithm, остовное дерево, максимальное остовное дерево и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Классические алгоритмы онлайн
Комментарии
Оставить комментарий
Классические алгоритмы онлайн
Термины: Классические алгоритмы онлайн