Лекция
Привет, мой друг, тебе интересно узнать все про mathcad в преподавании физики, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое mathcad в преподавании физики , настоятельно рекомендую прочитать все из категории Прикладная физика.
Наиболее любознательные учащиеся сталкиваются при изучении физики с характерной трудностью – недостатком математических знаний. Огромное число интересных задач, физическое содержание которых понятно, не могут быть решены, поскольку требуют знания производной, интеграла или дифференциальных уравнений. Например: учащиеся еще в 9-м классе знакомятся со вторым законом Ньютона и законом всемирного тяготения, однако этого недостаточно для расчета движения планет и космических кораблей. Хотя программой для физико-математических классов и предусмотрено изучение основ матанализа, однако, в средней школе вряд ли возможно овладеть техникой вычисления интегралов и решения диффуравнений в той степени, которая необходима для решения физических задач. Да и при наличии соответствующих знаний нужно иметь ввиду, что подавляющее большинство интегралов не вычисляются через элементарные и специальные функции, а аналитическое решение известно лишь для некоторых классов дифференциальных уравнений. Повсеместное распространение компьютеров дает возможность решать многие задачи численными методами, в основе которых – замена интегрирования суммированием и производных конечными разностями. В такой постановке задачи становятся доступными учащемуся. Единственное, что требуется – машина, умеющая считать.
Системы компьютерной математики Maple, Mathematica, Mathlab и Mathcad существенно облегчают диалог человека с компьютером при решении математических задач. Систему Mathcad выделяет среди вышеупомянутых систем чрезвычайно удобный интерфейс и превосходная графика. Для овладения Mathcadом, в отличие от языков программирования Pascal, Fortran не нужны ночные бдения в течение недель и месяцев. Метод решения конкретной задачи можно изучить прямо сейчас и тут же применять. Запоминать нужно минимальное количество сведений. Для написания программ с использованием Mathcadа требуется намного меньше времени, чем при использовании упомянутых языков программирования, благодаря большому набору встроенных функций. Все это важно для учащихся с психологической точки зрения, поскольку многими предметами учащиеся приучены к тому, что истинные знания и умения появятся не сразу, а когда-то потом, может быть через годы упорного труда. Происходит девальвация понятия “сейчас” и все откладывается на “потом”. А ведь жизнь не откладывается, она идет, она и есть то, что происходит сейчас. В этом смысле система Mathcad увеличивает цену полученных знаний, позволяет их применять, не откладывая интересующие вопросы в долгий ящик. Благодаря этому знания, полученные на уроках физики и математики, становятся мощным инструментом познания окружающего мира, а не набором сведений, необходимых для решения задач и головоломок на олимпиадах и вступительных экзаменах.
Учителю физики применение Mathcadа в учебном процессе дает возможность глубоко и наглядно осветить многие вопросы программы, а не ограничиваться описательной стороной дела.
Следует также иметь ввиду, что при традиционных методах преподавания, учащиеся хотя и получают полезные знания, но имеют весьма смутное представление о содержании и методах науки. Очень часто, наловчившись решать задачи про наклонную плоскость, линзы, электрические цепи с батарейками и лампочками и т.п., ученик думает, что это и есть физика. В этом смысле традиционные методы преподавания в какой-то степени дезориентируют учащегося. Применение систем компьютерной математики характерно для труда научного работника, поэтому использование Mathcadа в учебном процессе способствует профессиональной ориентации учеников, подумывающих о карьере ученого.
В гимназии есть два компьютерных класса, оснащенных современными компьютерами, и кроме того у подавляющего большинства учащихся физматкласса есть компьютеры дома. Это является материальной базой для внедрения системы Mathcad в учебный процесс. Программой обучения в физматклассе предусмотрено изучение основ Mathcadа в 10-м классе в первой четверти в течение 16 часов и постоянное использование Mathcadа на всем протяжении обучения в 10-х и 11-х классах. Ознакомительный курс заканчивается зачетом, на котором учащиеся должны продемонстрировать умение:
Последний пункт имеет особое значение, поскольку это основа численного интегрирования.
Типовой вариант заданий для зачета представлен на рис 1. В дальнейшем учащиеся применяют полученные знания для выполнения домашних заданий по математике и физике, а также изучают другие возможности Mathcadа по мере прохождения соответствующего материала на уроках математики, физики и информатики. Имеется ввиду дифференцирование и интегрирование, решение дифференциальных уравнений, построение трехмерных графиков и объемных фигур, программирование в системе Mathcad.

Начиная со второй четверти, в 10-м классе учащиеся не менее раза в неделю выполняют домашние задания по физике с использованием системы Mathcad. Выполненные задания раз в неделю представляются учителю на дискетах, либо отсылаются по электронной почте. Составной частью зачетов по физике по окончании 10-го класса и первого полугодия 11-го класса является решение физических задач с помощью системы Mathcad.
Для учащихся 9-го класса желающих продолжать учебу в физматклассе, в течение года, раз в неделю, проводились занятия по решению физических задач с помощью системы Mathcad. На этих дополнительных занятиях учащиеся овладевали системой Mathcad на уровне вышеприведенных требований зачета и программированием, а кроме того знакомились с графическим редактором CorelDRAW, необходимым для качественного оформления домашних работ. Об этом говорит сайт https://intellect.icu . Большую часть времени занимало решение задач, главным образом по механике (численное интегрирование уравнений движения).
По нашему мнению, лучшее представление о возможностях применения Mathcadа в условиях средней школы может дать набор задач решаемых учащимися. Обзор задач и комментариев к ним будет составлять основу дальнейшего изложения. Предполагается, что известная квалификация знакомящегося с этими строками, избавляет от необходимости приводить подробные условия и решения задач. Следует заметить, что ряд заслуживающих внимания тем не отражены в данном материале из-за недостатка места или технических возможностей, например: применение анимации для моделирования волновых процессов, движение небесных тел в поле двойных звезд, солнечный парус, трехмерное моделирование потенциала, движение в магнитном поле и т. д.
Образцы задач, предлагаемых учащимся, имеют целью продемонстрировать на конкретных примерах разнообразие математических средств Mathcadа, а выбор физической тематики произволен в том смысле, что хотя по всем разделам курса физики можно составить достаточно много интересных задач, полностью отразить программу курса физики – такой цели данный материал не имеет.
Вычисление средней квадратичной скорости молекул с помощью функции пользователя.
Наиболее целесообразный путь решения задачи – создать функцию пользователя. В формуле используется абсолютная температура, а в условии температуры даются в градусах Цельсия, кроме того, необходимо подсчитать массу молекулы. Нет необходимости самому отдельно вычислять абсолютную температуру и считать массу молекул, а достаточно подставить формулы с числами вместо аргументов в функцию пользователя. Как выглядит решение задачи средствами Mathcadа показано на рис. 2.

Способы распределения молекул по половинкам сосуда.
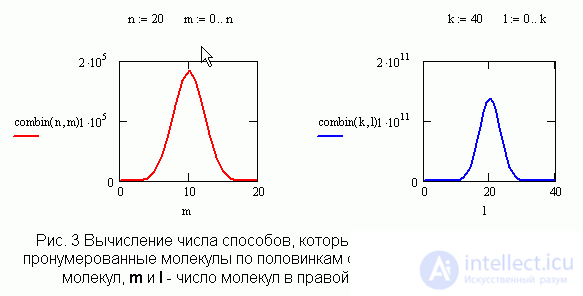
Для иллюстрации понятия наиболее вероятного состояния при изучении второго закона термодинамики рассматривают сосуд, в котором находятся пронумерованные молекулы и подсчитывают число способов, которым реализуется та или иная ситуация. Быстро и не мене наглядно можно получить результат средствами Mathcadа рис. 3. Графики дают представление о том, что наиболее вероятная ситуация соответствует равномерному распределению молекул. А число способов, которым реализуется равномерное распределение, дает представление о вероятности отклонения от равновесного состояния, если число молекул равно числу Лошмидта.
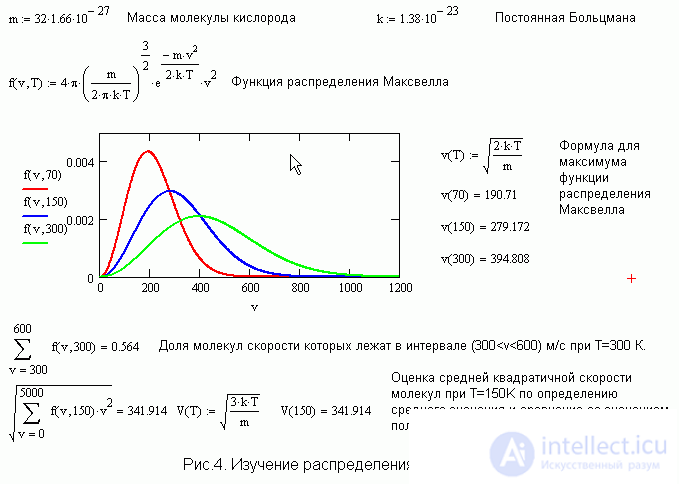
Распределение Максвелла.
Рис. 4 дает представление о качестве проработки данной темы, если в распоряжении ученика есть Mathcad. Можно изучить влияние температуры на форму и высоту кривой, а также на положение максимума функции распределения. С помощью суммирования можно посчитать долю молекул, обладающих скоростями в каком либо интервале, а также простым суммированием определить среднюю и среднюю квадратичную скорости молекул.
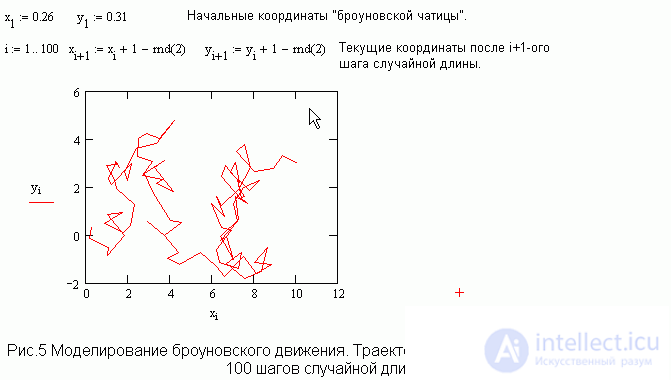
Броуновское движение.
Наличие генератора случайных чисел дает возможность моделировать движение броуновской частицы. Рис. 5 дает представление о том, как просто и быстро можно получить нужный результат.
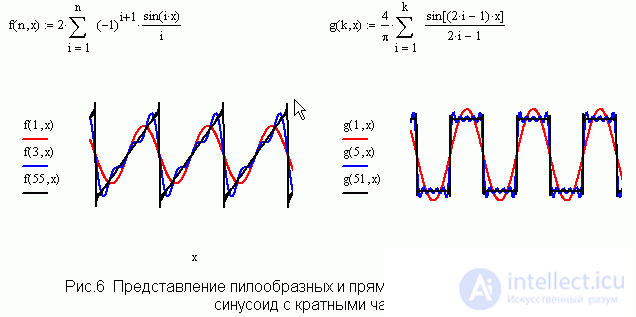
Гармонический анализ.
Когда рассказывают ученикам о тембре звука, говорят о том, что наличие обертонов определяет окраску звука. Добавляют также, что обертоны – это колебания с частотами кратными основной. Но как получить несинусоидальное колебание с помощью набора гармоник учащиеся могут только догадываться. Рис. 6 показывает, как решается эта задача с помощью Mathcadа. Совершенно четко видно, что, складывая в определенной пропорции гармоники с кратными частотами, можно получить колебания нужной формы, и чем больше число гармоник, тем отчетливее проступает форма нужного колебания. После того, как наглядно на качественном уровне понят смысл гармонического анализа, наиболее любознательным учащимся можно сообщить формулы для коэффициентов разложения в ряд Фурье. С помощью Mathcadа учащийся может вычислить необходимые интегралы.
Моделирование колебаний математического маятника.
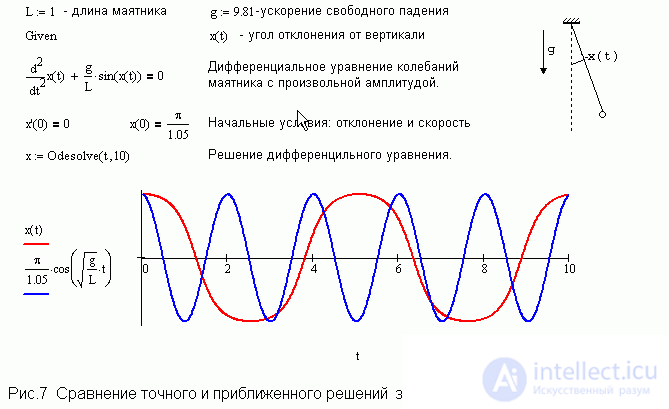
При выводе формулы для периода колебаний математического маятника отмечают, что данная формула справедлива при малых амплитудах колебаний. А что будет при больших амплитудах колебаний? Mathcad позволяет всесторонне исследовать проблему. Можно численно получить решения точного и приближенного дифференциальных уравнений колебаний математического маятника, а затем сравнить полученные результаты. В случае малых амплитуд согласие между приближенным и точным решением действительно хорошее, графики обоих решений налагаются друг на друга в течение нескольких периодов. А в случае больших амплитуд, как показывает рис.7, расхождение и количественное, и качественное. При больших амплитудах колебания явно не синусоидальные. Таким образом, учащийся не только получает представление о точности приближенной формулы, но может получить результат для произвольных амплитуд.
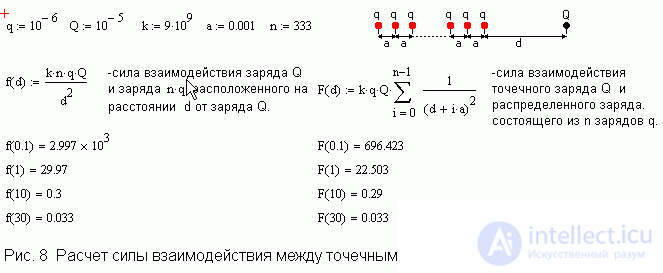
Применение принципа суперпозиции для расчета сил электростатического взаимодействия в случае большого числа зарядов.
В школьном курсе электростатики ограничиваются изучением взаимодействия точечных зарядов, а о решении вопросов расчета взаимодействия заряженных тел не говорится, хотя с идейной точки зрения задача довольно проста: нужно разбить тело на малые части и применить принцип суперпозиции. Разумеется, такой способ возможен при наличии соответствующих вычислительных средств. Рис. 8 и 9 показывают решение двух электростатических задач средствами Mathcadа. Эти задачи могут служить промежуточным этапом на пути овладения методов решения задач с произвольным распределением зарядов. Очень полезно сравнивать результаты с теми, что получены применением закона Кулона, в случае если бы группа зарядов находилась в одной точке, на расстоянии x от выделенного заряда. При больших расстояниях х от системы результаты, как и следовало ожидать, близки. Таким образом, мы получаем иллюстрацию к критерию точечности заряда: заряды можно считать точечными, если расстояние между взаимодействующими зарядами велико по сравнению с размерами зарядов. После решения данных задач можно легко рассчитать силы взаимодействия между заряженным стержнем и точечным зарядом. Решение подобных задач дает хороший материал для изучения впоследствии понятия интеграла.

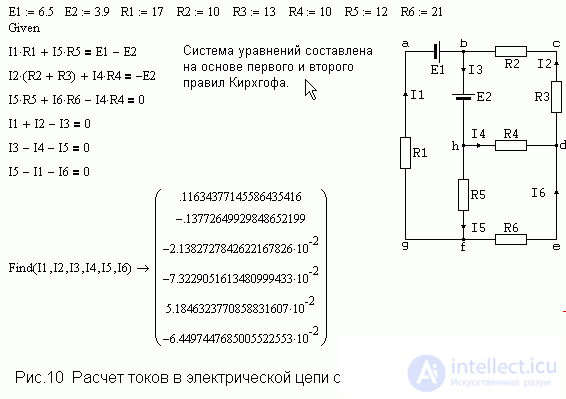
Расчет электрической цепи с помощью правил Кирхгофа.
Применение Mathcadа весьма эффективно при решении задач, где необходимо применение систем линейных уравнений, например, расчет электрических цепей. Хотя с математической точки зрения задача проста, однако большой объем вычислительной работы делает задачу в случае, например, 10 уравнений технически невыполнимой из-за практически неизбежных ошибок. Написать систему из 10 уравнений можно, а вот решить… Используя встроенную функцию Mathcadа, можно без труда справится с подобной задачей. Рис. 10 иллюстрирует объем необходимой работы при решении задач подобного типа.
Нелинейные элементы в электрической цепи.
Поверхностное знание школьной программы создает иллюзию, что самым важным законом электромагнетизма является закон Ома. Его место в школьном курсе определяется тем, что он выражается простой формулой. А между тем линейная зависимость между током и напряжением скорее исключение, чем правило, и наиболее интересные и плодотворные применения электричества начинаются там, где нарушается закон Ома. В качестве примера применения Mathcadа рассмотрим задачу о последовательном соединении омического сопротивления и нелинейного элемента, ВАХ которого описывается степенной функцией (степенная ВАХ характерна для варистора). С математической точки зрения, трудность данной задачи связана с необходимостью решения уравнения, в котором неизвестная может быть в нецелой степени большей двух. Mathcad позволяет без труда численно решить уравнение и определить напряжение на элементах схемы, а также построить график зависимости напряжения на нелинейном элементе U от внешнего напряжения Е. Рис. 11 показывает, как можно изучать нелинейность средствами Mathcadа. Полученный график свидетельствует о том, что нелинейный элемент стабилизирует напряжение, т.е. если Е меняется в 5 раз, то напряжение U изменяется в 3 раза.

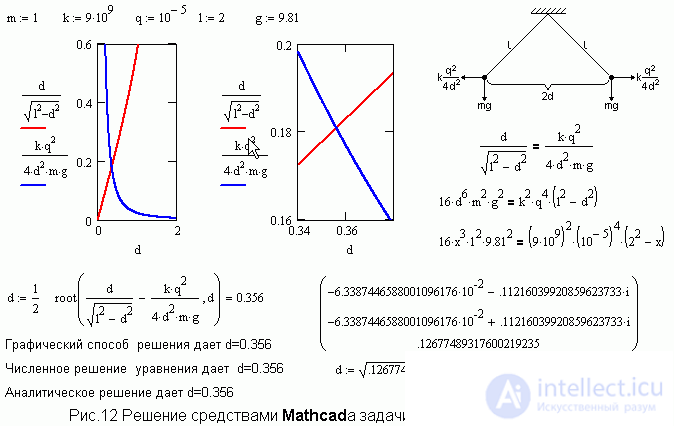
Задача о зарядах на нитях.
Многие поколения учащихся решали задачу об отталкивающихся заряженных шариках, подвешенных на нитях. Угол между нитями и длина нитей заданы и нужно найти либо величину заряда, либо массу шарика. Однако если видоизменить постановку задачи и считать неизвестным угол между нитями или расстояние между шариками, а массу и заряд шариков, а также длину нити считать известными, то задача становится неразрешимой для учащегося из-за кубического уравнения. С помощью Mathcadа уравнение можно решить либо аналитически, либо численно, либо графически. Разные варианты решения данной задачи представлены на рис. 12.
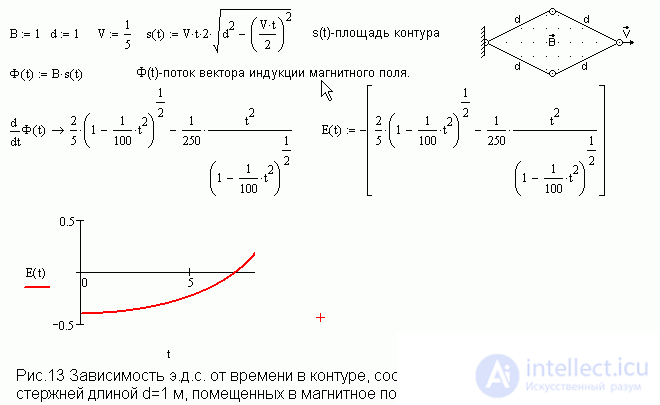
Э. Д. С. в деформируемом контуре, помещенном в магнитное поле.
На рис.13 представлен пример использования Mathcadа для нахождения производной и построения графика зависимости э. д. с. контуре от времени. Ясно, что задачу можно усложнить, задавая произвольную зависимость от времени и меняющееся магнитное поле, однако и в этом случае объем работы ненамного возрастает. Из этого примера видно, что задачи об электромагнитной индукции можно бесконечно разнообразить, а не ограничиваться набившими оскомину изменением площади прямоугольного контура и равномерно вращающимися в магнитном поле рамкой и стержнем.
Влияние сжимаемости вода на глубину мирового океана.
В силу чрезвычайно важности суммирования приведем еще одну задачу на эту тему. Средняя глубина Мирового океана 4000 м. Хотя учащимся часто приходится слышать о малой сжимаемости воды, подсчитаем (оценим), как изменился бы уровень океана, если бы сжимаемость воды была бы равна нулю. Разобьем толщу воды на слои (высотой, например 1 метр) и подсчитаем изменение высоты каждого слоя вследствие давления вышележащих слоев. Решение задачи представлено на рис. 14. Результаты решения показывают, что сжимаемость воды самым существенным образом повлияла на площадь суши.

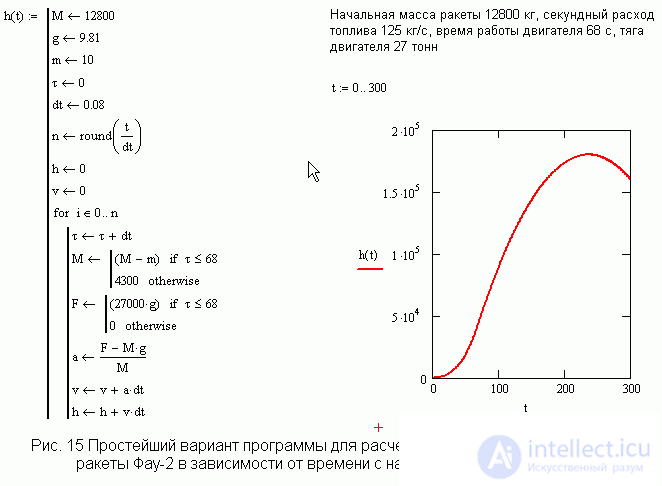
Моделирование полета ракеты Фау-2.
Беспредельные возможности для создания новых задач дает программирование. В Mathcadе есть все необходимое написания изящных программ. В литературе есть подробные данные о ракете Фау-2, что позволяет моделировать полет ракеты и сравнить с параметрами реального полета. Даже столь простая программа, как представлена на рис. 15, довольно точно отражает полет настоящей ракеты. Компьютер позволяет, не ломая голову над дифференциальными уравнениями описывающих движение переменной массы, на основе простейших знаний, которыми располагает учащийся 9-го класса, исследовать полет реальной ракеты. Надо ли говорить, что без компьютера возможно лишь качественное описание реактивного движения как иллюстрации закона сохранения импульса.
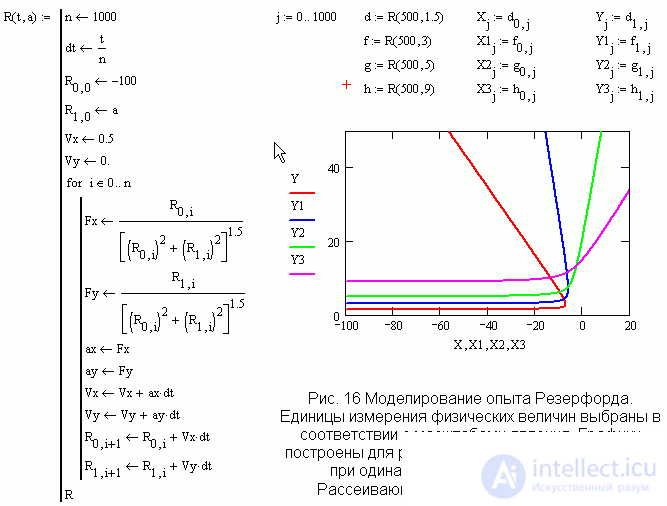
Моделирование опытов Резерфорда.
Гораздо глубже можно понять значение открытия Резерфорда, если на основании уравнений движения построить модель движения альфа частицы в поле ядра. Только с помощью расчета можно убедится, что большие отклонения альфа частицы могут случаться только в том случае, если заряд сконцентрирован в очень маленькой области с размерами порядка нескольких ферми. Томсоновская модель атома ни при каких условиях не может дать больших отклонений. Все это можно получить только на основе расчета, любые качественные аргументы здесь бессильны. На рис.16 представлена программа и результаты расчетов движения альфа частиц. В формулах используются единицы измерения, характерные для масштабов изучаемого явления.
В связи с повсеместным распространением компьютеров и появлением систем компьютерной математики, в частности Mathcadа, можно и нужно существенно изменить характер и уровень преподавания школьных курсов физики и математики. Целесообразность широкого применения Mathcadа можно мотивировать следующим образом:
С учетом вышеизложенного представляется необходимой разработка новых задач, по крайней мере, для учащихся физматклассов и физматшкол. Представленный материал можно рассматривать как идею создания сборника задач по физике для физматшкол, изложенную на предметном уровне.
Как ты считаеешь, будет ли теория про mathcad в преподавании физики улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое mathcad в преподавании физики и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Прикладная физика
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Прикладная физика
Термины: Прикладная физика