Лекция
Привет, Вы узнаете о том , что такое плоская укладка графа, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое плоская укладка графа, укладка графа , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
В данной статье будет рассмотрена задача на графах о возможности нарисовать тот или иной граф без самопересечений. То есть нарисовать граф так, чтобы его ребра не имели общих внутренних точек. Поставленную задачу принято называть задачей о плоской укладке графа.
Область применения результата, который мы получим, очень обширна. Одна из них — это изготовление электронных схем. Электрические цепи печатным способом наносятся на плату из изолирующего материала. Так как наносимые цепи не изолированы, то они не должны пересекаться. Отсюда вытекает вопрос, как расположить контакты на схеме, чтобы можно было без пересечений нанести цепи на плату. А если так сделать нельзя, то каким минимальным числом плат (слоев графа) можно обойтись.
Мы коснемся только первой части вопроса и ответим, когда и как можно нарисовать граф без самопересечений.
Плоский граф — это граф, нарисованный таким образом, что его ребра не пересекаются. Говорят, что граф допускает плоскую укладку, если его можно нарисовать как плоский. Также плоские графы называют планарными.
Граф, изображенный на рис. 1, плоский:
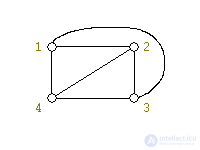
Существуют и непланарные графы. На рис. 2 показаны два таких графа: полный пятивершинник и полный двудольный граф. Для них есть специальные обозначения: K5 и K3,3соответственно.

Двудольный граф — это граф, вершины которого разбиты на две доли (части), а ребра проходят только между вершинами из разных частей.
В планарном графе можно говорить не только о вершинах и ребрах, но и о гранях.
Грань — это часть плоскости, окруженная простым циклом и не содержащая внутри себя других элементов графа.
Внешняя грань — это вся плоскость, окружающая плоский граф.
Пример планарного графа. Синим контуром обозначены грани, за исключением внешней грани (всего 5 граней). Обратите внимание, что внутри грани могут содержаться другие ребра и вершины.
Определение:
Граф называется планарным (англ. planar graph), если он обладает укладкой на плоскости. Плоским (англ. plane graph, planar embedding of the graph) называется граф уже уложенный на плоскости.
Определение:
Плоский граф разбивает плоскость на несколько областей, называемых гранями (англ. faces). Одна из граней не ограничена, ее называют внешней (англ. external) гранью, а остальные — внутренними (англ. unbounded) гранями.
Для плоских графов есть простое соотношение, называемое формулой Эйлера: V−E+F=2 , где V — вершины, E — ребра, F — грани.
Это свойство позволяет в некоторых случаях просто доказывать непланарность некоторых графов, например непланарность K5 и K3,3
Понятно, что любой граф, содержащий подграф K5 или K3,3 непланарен. Оказывается, верно и обратное утверждение, но для его формулировки потребуется вспомогательное определение:
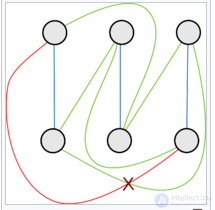
Полный двудольный граф K3,3 . Этот граф непланарен, и его не получится изобразить на плоскости без пересечений ребер.
Определение:
Введем отношение R следующим образом: два графа находятся в отношении R , если один можно свести к другому заменой вершины степени 2 на ребро между вершинами смежными ей, или наоборот, добавлением вершины степени два на ребро (см. картинку).
Отношением гомеоморфизма (или топологической эквивалентности) назовем транзитивное замыкание отношения R : R *.

Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K5 и K3,3 : теорема Понтрягина-Куратовского.
Теорема:
В трехмерном евклидовом пространстве любой граф укладывается.
Доказательство:Все вершины произвольного графа G помещаем в различных точках координатной оси OX . Об этом говорит сайт https://intellect.icu . Рассмотрим пучок плоскостей, проходящих через ось OX , и зафиксируем |E| различных таких плоскостей. Теперь каждое ребро (u,v) изобразим полуокружностью, проходящей в соответствующей плоскости через вершины u,v . Ясно, что различные ребра не будут пересекаться кроме как в общих вершинах.
Задача. Определить, является ли граф планарным, и, если да, то произвести его плоскую укладку.
Замечание. Если на ребра планарного графа нанести произвольное число вершин степени 2, то он останется планарным; равным образом, если на ребра непланарного графа нанести вершины степени 2, то он планарным не станет.
В конце 1920-х годов Куратовский в Польше и Л.С. Понтрягин в СССР независимо доказали поразительную теорему, показывающую, что мешает графу быть планарным.
Граф планарен тогда и только тогда, когда он не содержит в качестве частей графы К5 и К3,3 (быть может с добавочными вершинами степени 2).
Мы опустим достаточно сложное доказательство этой теоремы. Заинтересованный читатель сможет найти его в . Однако не следует думать, что раз трудностей всего две, то непланарных графов мало: при росте числа вершин непланарны почти все графы.
Рассмотренный критерий очень трудоемок для проверки и поэтому представляет лишь теоретический интерес.
Для плоской укладки графа и попутной проверки, планарен ли он, удобно пользоваться гамма-алгоритмом.
На вход подаются графы, обладающие следующими свойствами:
Если нарушено свойство (1), то граф нужно укладывать отдельно по компонентам связности.
Если нарушено свойство (2), то граф — дерево и нарисовать его плоскую укладку тривиально.
Случай нарушения свойства (3) рассмотрим более подробно. Если в графе есть мостики, то их нужно разрезать, провести отдельно плоскую укладку каждой компоненты связности, а затем соединить их мостиками. Здесь может возникнуть трудность: в процессе укладки концевые вершины мостика могут спрятаться внутри плоского графа. Нарисуем одну компоненту связности и будем присоединять к ней другие последовательно. Каждую новую компоненту связности будем рисовать в той грани, в которой лежит концевая вершина соответствующего мостика. Так как граф связности мостиками компонент связности является деревом, мы сумеем получить плоскую укладку.
Сначала изложим алгоритм на конкретном примере. Пусть дан граф G (см. рис. 3).
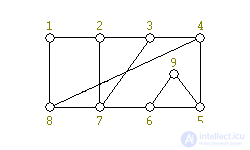
Инициализация алгоритма производится так: выбираем любой простой цикл; в нашем примере {1, 2, 3, 4, 5, 6, 7, 8} и получаем две грани: Γ1 — внешнюю и Γ2 — внутреннюю (см. рис. 4).

Обозначим выбранный цикл как G′. На каждом шаге будем строить множество сегментов. Каждый сегмент S относительно уже построенного графа G′ представляет собой одно из двух:
Те вершины, которые одновременно принадлежат G′ и какому-то сегменту, назовем контактными. Для нашего примера сегменты и вершины изображены на рис. 5. Контактные вершины обведены в квадрат.
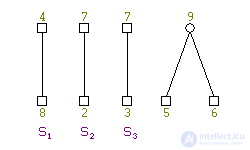
Если бы в каком-нибудь сегменте не было ни одной контактной вершины, то граф до разрезания был бы несвязный; если бы была только одна, то граф имел бы мостик. Эти возможности заранее исключены, так что каждый сегмент имеет не менее двух контактных вершин. Поэтому в каждом сегменте имеется цепь между любой парой таких вершин.
Если все контактные вершины сегмента S имеют номера вершин какой-то грани Γ, то мы будем говорить, что грань Γ вмещает этот сегмент и обозначать S⊂Γ. Может быть имеется не одна такая грань, вмещающая сегмент S, множество таких граней обозначим Γ(S), а их число |Γ(S)|.
Общий шаг алгоритма следующий: обозреваются все сегменты Si и определяются числа |Γ(Si)|. Если хоть одно из них равно 0, то граф не планарен, конец. Иначе, выбираем сегмент, для которого число |Γ(S)| минимально, или один из множества, если таких сегментов несколько. В этом сегменте найдем цепь между двумя контактными вершинами и уложим ее в любую из граней множества Γ(S), совместив контактные вершины сегмента с соответствующими вершинами грани. При этом данная грань разобьется на две. Уже уложенная часть графа G′ по количеству ребер и вершин увеличится, а сегмент, из которого вынута цепь, исчезнет или развалится на меньшие с новыми контактными вершинами, ведущими к вершинам G′.
В результате повторения общего шага либо будет получена плоская укладка, когда множество сегментов станет пустым, либо будет получено, что граф G не является планарным.
Вернемся к нашему примеру. Пока для любого i: Si⊂{Γ1, Γ2}, |Γ(Si)| = 2. Поэтому возьмем первый по номеру сегмент Si и в нем первую попавшеюся цепь {4, 8}; вставим эту цепь в грань Γ2. Получим увеличенную часть G′ и уменьшенную систему сегментов (см. рис. 6 a, b).
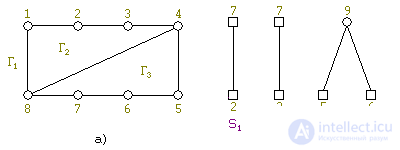
Определим какие грани вмещают новые сегменты. Теперь сегменты S1 и S2 вмещаются только в одну грань Γ1, в то время, как сегмент S3 вмещается в две грани Γ1 и Γ3. Поэтому берем S1. Возьмем в нем цепь между контактными вершинами, например, {2, 7}, и уложим ее в Γ1. Получим увеличенную часть G′ и уменьшенную систему сегментов (см. рис. 7 a, b).
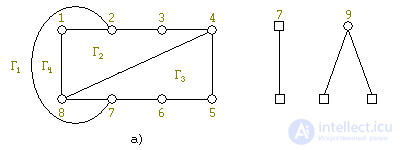
Продолжая таким образом, в итоге получим плоскую укладку G (см. рис. 8).
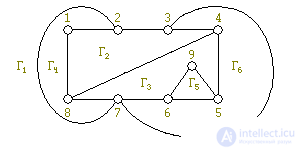
Еще раз опишем гамма-алгоритм компактно и займемся его обоснованием.
Гамма-алгоритм
Вначале докажем ряд впомогательных утверждений.
Для любого сегмента |Γ(S)| ≤ 2.
Доказательство. Действительно, если все контактные вершины одного сегмента принадлежат некоторой грани Γ (точнее, циклу, окружающему эту грань), то они могут принадлежать все вместе только одной еще грани, а именно внутренней или внешней. Ч. т. д.
Назовем сегменты S1 и S2 конфликтующими относительно уже уложенной части, если:
Конфликтующие сегменты S1 и S2 обладают следующим свойством: если |Γ(S1)| = 2 и |Γ(S2)| = 2, то Γ(S1) = Γ(S2).
Доказательство. Действительно, в противном случае, имея по определению одну общую вмещающую грань Γ3, они бы имели еще по собственной вмещающей грани Γ1 и Γ2соответственно. Тогда любые цепи из S1 и S2 могли бы разместиться в Γ1 и Γ2 соответственно, а значит и в Γ3, причем без пересечения; следовательно S1 и S2 не были бы конфликтующими. Противоречие. Лемма доказана.
Замечание. Из доказанной леммы следует, что, имея сегмент S1, и еще сегмент S2, конфликтующий с S1, затем сегмент S3, конфликтующий с S2 (но не с S1) и т. д., причем каждый вмещается в две грани, то эти грани общие для всех сегментов последовательности, и можно размещать цепь L1 из S1 в первую грань Γ1, L2 из S2 в Γ2, L3 из S3 снова в Γ1 и т. д. до конца последовательности. Если цепочка сегментов замыкается в цикл четной длины, то проблем не будет; если в нечетный цикл, то в конце окажется, что два конфликтующих сегмента нужно разместить без пересечений в общую грань, что невозможно.
Сейчас нам понадобится в качестве вспомагательного утверждения теорема Кенига, которая полезна при решении и многих других задач.
В графе все циклы четные тогда и только тогда, когда граф является двудольным.
Доказательство.
Достаточность. Рассмотрим двудольный граф. Начнем цикл в верхней доли. Нужно пройти по четному числу ребер, чтобы подняться снова в верхнюю долю. Следовательно, при замыкании цикла число ребер будет четным.
Необходимость. Если граф несвязный, то проведем доказательство отдельно для каждой компоненты. Пусть граф связный и все циклы в нем четные. Выделим произвольную вершину v0и найдем произвольные цепи между v0 и всеми остальными вершинами (например, самые короткие алгоритмом Дейкстры). Если одна цепь (v0, vi) нечетной длины, то и любая цепь (v0, vi) нечетная, иначе бы эти цепи образовали нечетный цикл. Аналогично, если (v0, vi) — четная, то и любая (v0, vi) — четная. Разобьем вершины на две доли: в одну войдет вершина v0 и все, находящиеся от v0 на четном расстоянии; в другую долю поместим все вершины, находящиеся от v0 на нечетном расстоянии. Если вершины u1 и u2 принадлежат одной доле, то между ними не может быть ребра, иначе это ребро вместе с цепями (v0, u1) и (v0, u2) образовали бы нечетный цикл. Ч. т. д.
Частичной укладкой G′ планарного графа G называется граф, который можно получить из какой-нибудь укладки графа G на плоскости удалением каких-то ребер и вершин. Таким образом, частичная укладка — это правильное начало укладки, в ней еще не сделано ошибок.
В частичной укладке G′ сопоставим каждому сегменту вершину в некотором постороннем служебном графе A(G′), где вершины соединяются ребрами, если соответствующие сегменты являются конфликтующими.
Если результатом некоторого шага работы гамма-алгоритма является частичная укладка G′ планарного графа G такая, что |Γ(S)| = 2 для любого сегмента S относительно G′, то A(G′) — двудольный граф.
Доказательство. Пусть A(G′) — не двудольный, тогда по теореме Кенига в нем есть цикл нечетной длины. По Лемме 2 все вершины этого цикла вмещаются ровно двумя гранями. Поскольку цикл нечетный, мы не сможем уложить эти сегменты в две грани. Противоречие. Лемма доказана.
Ну вот, мы наконец-то подошли к тому, чтобы доказать нужную теорему.
Гамма-алгоритм корректен, то есть, если G — планарный граф, то результатом каждого шага гамма-алгоритма является частичная укладка G′.
Доказательство. Докажем индукцией по числу шагов.
База индукции очевидна: результат инициализации есть плоская укладка, так как уложенный цикл будет в любой укладке.
Пусть граф G′k−1, полученный на (k−1)-м шаге, является частичной укладкой. На текущем шаге к нему присоединится цепь L: G′k = G′k−1 ∪ L. Докажем, что граф G′k — тоже частичная укладка. Среди сегментов на текущем шаге нет такого S, что |Γ(S)| = 0, иначе G′k−1 не был бы частичной укладкой. Значит, либо существует S такой, что |Γ(S)| = 1, либо все S таковы, что |Γ(S)| = 2.
Первый случай означает, что укладка S в Γ неизбежна, так что граф G′k после добавления цепи из S останется частичной укладкой. Во втором случае построим граф A(G′k−1), по Лемме 3 он двудольный. Возьмем его связную компоненту A′, этот граф тоже двудольный. Для сегментов из A′ имеются ровно две грани Γ1 и Γ2, вмещающие их. Раскидаем сегменты A′ по граням Γ1 и Γ2 попеременно. Это необходимо сделать в каждой частичной укладке, следовательно получена частичная укладка.
Фактически, основой последней части доказательства было, что если граф A(G′k−1) — двудольный, то после удаления части ребер и вершин граф A(G′k) тоже двудольный. Таким образом, в результате каждой итерации для планарного графа частичная укладка увеличивается, в конце мы получим плоскую укладку.
Выводы из данной статьи про плоская укладка графа указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое плоская укладка графа, укладка графа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов