Лекция
Привет, сегодня поговорим про связный граф, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое связный граф, не связный граф, сильносвязный граф , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
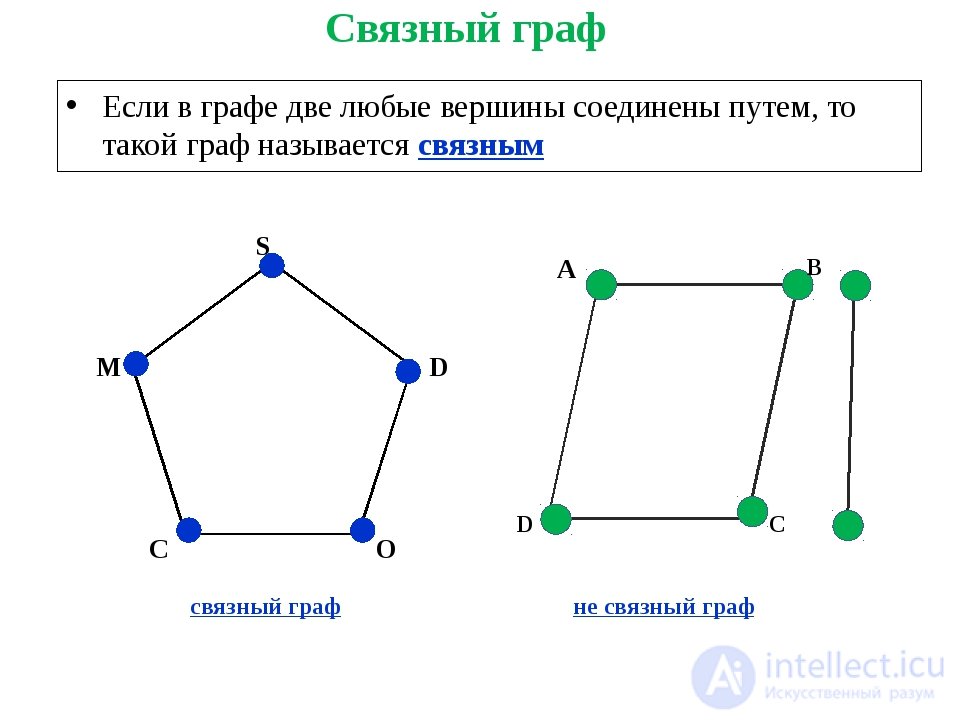
связный граф — граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует как минимум один путь.
Определение 11.1. Маршрутом в графе называется последовательность вершин и ребер, которая обладает следующими свойствами:
1. она начинается и заканчивается вершиной;
2. вершины и ребра в ней чередуются;
3. любое ребро последовательности имеет своими концами две вершины: непосредственно предшествующую ему в этой последовательности и следующую сразу за ним.
Первая и последняя вершины в этой последовательности называются началом и концом маршрута. Проиллюстрировать данное определение можно на примере путешествия между городами: сначала мы записываем начальный город нашего путешествия, потом дорогу, по которой из него выезжаем, потом город, в который прибываем, потом следующую дорогу, по которой едем дальше и т.д., пока не закончим путешествие в каком-нибудь городе, который и будет записан последним. Заметим, что согласно определению маршрута в нем одна и та же вершина или ребро могут встречаться несколько раз. Также можно отметить, что для задания маршрута достаточно указать только последовательность вершин, поскольку по ней последовательность ребер восстанавливается однозначно. Хотя в случае мультиграфа определение маршрута не меняется, но задать сам маршрут одной лишь последовательностью вершин может не получиться, поскольку для некоторых пар вершин ребро, соединяющее их, однозначно не определяется.
Определение 11.2. Путем называется такой маршрут, в котором никакое ребро не встречается дважды. Иногда его также называют цепью.
Определение 11.3. Граф называется связным если между любыми двумя его вершинами существует маршрут. В противном случае граф называется несвязным.
Определение 11.4. Любой несвязный граф состоит из нескольких связных графов, каждый из которых называется компонентой связности графа. В частности у связного графа ровно одна компонента связности.
Теорема 1. Граф на n вершинах, степень каждой из которых не менее (n − 1)/2, связен.
Доказательство. Предположим, что данный граф не является связным. Рассмотрим одну из его компонент связности и выберем в ней произвольную вершину. Поскольку эта вершина соединена не менее, чем с  другими вершинами, то всего вместе с ней в этой компоненте связности не менее
другими вершинами, то всего вместе с ней в этой компоненте связности не менее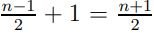 вершин. Аналогично в любой другой компоненте связности не менее
вершин. Аналогично в любой другой компоненте связности не менее 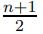 вершин. Поскольку несвязный граф имеет хотя бы две компоненты связности, то количество вершин в этих двух компонентах не менее
вершин. Поскольку несвязный граф имеет хотя бы две компоненты связности, то количество вершин в этих двух компонентах не менее 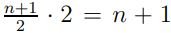 , а это противоречит условию, что в графе n вершин. Значит сделанное предположение неверно и граф является связным.
, а это противоречит условию, что в графе n вершин. Значит сделанное предположение неверно и граф является связным.
Теорема 2. Связный граф, в котором степень каждой вершины четна, при удалении любого ребра остается связным.
Доказательство. Пусть мы удалили ребро, которое соединяло вершины A и B. Если после этого вершины A и B оказались в разных компонентах связности, то рассмотрим компоненту связности 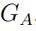 , содержащую вершину A. Поскольку количество ребер, выходящих из вершины A, уменьшилось на единицу, то степень вершины A также уменьшилась на единицу и стала нечетной, а степени всех остальных вершин в
, содержащую вершину A. Поскольку количество ребер, выходящих из вершины A, уменьшилось на единицу, то степень вершины A также уменьшилась на единицу и стала нечетной, а степени всех остальных вершин в 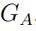 остались четными. Но это противоречит тому, что в любом графе количество нечетных вершин четно. (Это утверждение верно и для любой компоненты связности графа, поскольку сама по себе она тоже является графом.) А значит вершины A и B не могли оказаться в разных компонентах связности. Однако если вершины A и B оказались в одной компоненте связности, то существует маршрут M их соединяющий. Пусть X и Y — две произвольные вершины графа. Тогда между ними до удаления ребра существовал маршрут. Если в этом маршруте не содержалось ребра AB, то и в получившемся графе эти вершины связаны тем же маршрутом. Если же в в нем содержалось ребро AB один или несколько раз, то в любом месте, где оно появлялось, его вместе с вершинами A и B можно заменить на маршрут M, проходимый в прямом или обратном порядке в зависимости от того, проходилось ли ребро AB от вершины A к вершине B или наоборот. Но это означает, что граф остался связным.
остались четными. Но это противоречит тому, что в любом графе количество нечетных вершин четно. (Это утверждение верно и для любой компоненты связности графа, поскольку сама по себе она тоже является графом.) А значит вершины A и B не могли оказаться в разных компонентах связности. Однако если вершины A и B оказались в одной компоненте связности, то существует маршрут M их соединяющий. Пусть X и Y — две произвольные вершины графа. Тогда между ними до удаления ребра существовал маршрут. Если в этом маршруте не содержалось ребра AB, то и в получившемся графе эти вершины связаны тем же маршрутом. Если же в в нем содержалось ребро AB один или несколько раз, то в любом месте, где оно появлялось, его вместе с вершинами A и B можно заменить на маршрут M, проходимый в прямом или обратном порядке в зависимости от того, проходилось ли ребро AB от вершины A к вершине B или наоборот. Но это означает, что граф остался связным.
Теорема 3. Если из полного графа на n вершинах удалить не более n − 2 ребер, то граф останется связным.
Доказательство. Докажем, что для разделения полного графа на несколько компонент связности необходимо удалить более n − 2 ребер, из этого и будет следовать утверждение теоремы. Предположим, что мы удалили некоторое количество ребер, в результате чего образовалось несколько компонент связности. Пусть в одной из них оказалось k вершин, где 1 6 k 6 n − 1. Во всех остальных компонентах (может одной, может нескольких) оказалось n − k вершин. В полном графе каждая из k вершин была соединена ребром с каждой из этих n − k вершин. Об этом говорит сайт https://intellect.icu . Поскольку теперь эти ребра исчезли, то количество ребер, выходящих из каждой из k вершин уменьшилось хотя бы на n − k, а общее количество ребер уменьшилось на k(n − k). Осталось показать, что пришлось удалить более n − 2 ребер, т.е. k(n − k) > n − 2. Для этого рассмотрим разность k(n − k) − (n − 2).
Имеем:
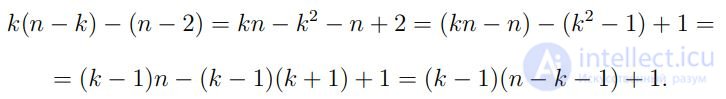
Поскольку 1 ≤ k ≤ n − 1, то каждая из скобок (k − 1) и (n − k − 1) неотрицательна, а значит разность k(n−k)−(n−2) больше 0. Тем самым мы доказали, что количество ребер, которое необходимо удалить из полного графа, чтобы сделать его несвязным, больше n−2, откуда и следует утверждение теоремы.
Прямым применением теории графов является теория сетей — и ее приложение — теория электронных сетей. Например, все компьютеры, включенные в сеть Интернет, образуют связный граф, и хотя отдельная пара компьютеров может быть не соединена напрямую (в формулировке для графов — не быть соединены ребром), от каждого компьютера можно передать информацию к любому другому (есть путь из любой вершины графа в любую другую).
В ориентированных графах различают несколько понятий связности.
Ориентированный граф называется сильно-связным, если в нем существует (ориентированный) путь из любой вершины в любую другую, или, что эквивалентно, граф содержит ровно одну сильно связную компоненту.
Ориентированный граф называется слабо-связным, если является связным неориентированный граф, полученный из него заменой ориентированных ребер неориентированными.
Здесь приведены некоторые критериальные (эквивалентные) определения связного графа:
Граф называется односвязным (связным), если:
Ориентированный граф называется сильно связным или сильным, если для любых двух различных вершин Xi и Xj существует по крайней мере один путь, соединяющий Xi с  . Это определение означает также, что любые две вершины такого графа взаимно достижимы.
. Это определение означает также, что любые две вершины такого графа взаимно достижимы.
Ориентированный граф называется односторонне связным или односторонним, если для любых двух различных вершин Xi и Xj существует по крайней мере один путь из Xi в Xj или из Xj в Xi (или оба одновременно).
Ориентированный граф называют слабо связным или слабым, для любых двух различных вершин графа существует по крайней мере один маршрут, соединяющий их.
Если для некоторой пары вершин орграфа не существует маршрута, соединяющего их, то такой орграф называется несвязным.
Граф приведенный на рис. 1.7(а), как легко проверить, сильно связанный. Граф, показанный па рис. 1.7(б), не является сильным (так как в нем нет пути из х1, в х3), но односторонне связный. Граф, изображенный на рис. 1.7(в), не является ни сильным, ни односторонним, поскольку в нем не существует путей от х2 к х5 и от х5 к х2. Он — слабо связный. Наконец, граф, приведенный на рис. 1.7(г), является несвязным.
Пусть дано некоторой свойство Р, которым могут обладать графы. Максимальным подграфом графа G относительно свойства Р называется порожденный подграф 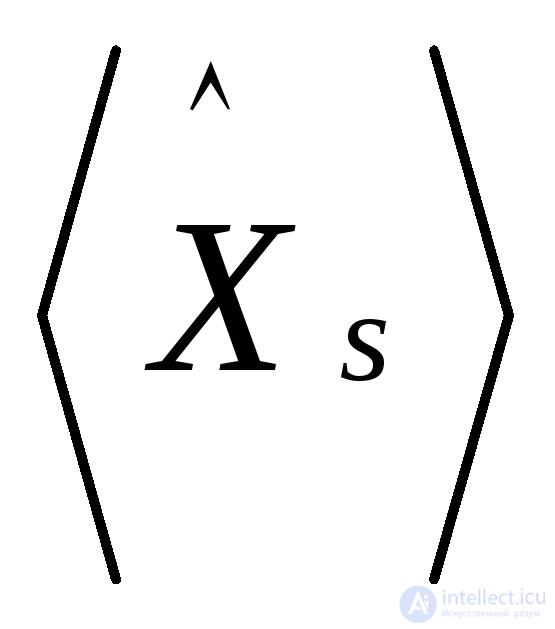 графа G, обладающий этим свойством и такой, что не существует другого порожденного подграфа , у которого
графа G, обладающий этим свойством и такой, что не существует другого порожденного подграфа , у которого 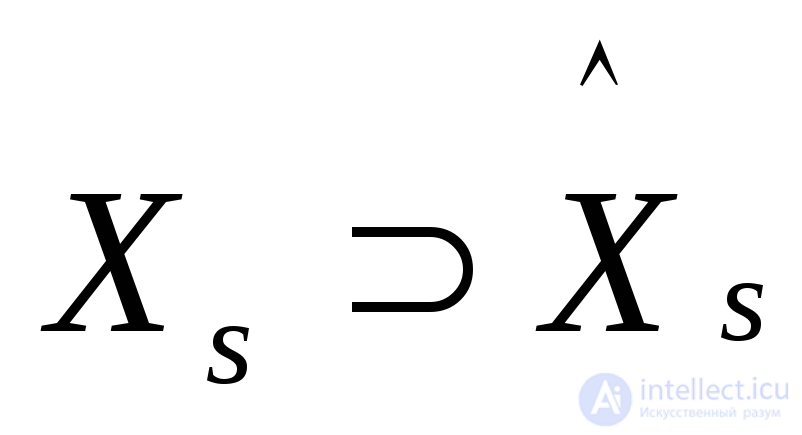 , и который также обладает свойством Р. Так, например, если в качестве свойства Р взята сильная связность, то максимальным сильным подграфом графа С является сильный подграф, который не содержится в любом другом сильном подграфе. Такой подграф называется сильной компонентой графа С. Аналогично, односторонняя компонента представляет собой односторонний максимальный подграф, а слабая компонента — максимальный слабый подграф.
, и который также обладает свойством Р. Так, например, если в качестве свойства Р взята сильная связность, то максимальным сильным подграфом графа С является сильный подграф, который не содержится в любом другом сильном подграфе. Такой подграф называется сильной компонентой графа С. Аналогично, односторонняя компонента представляет собой односторонний максимальный подграф, а слабая компонента — максимальный слабый подграф.
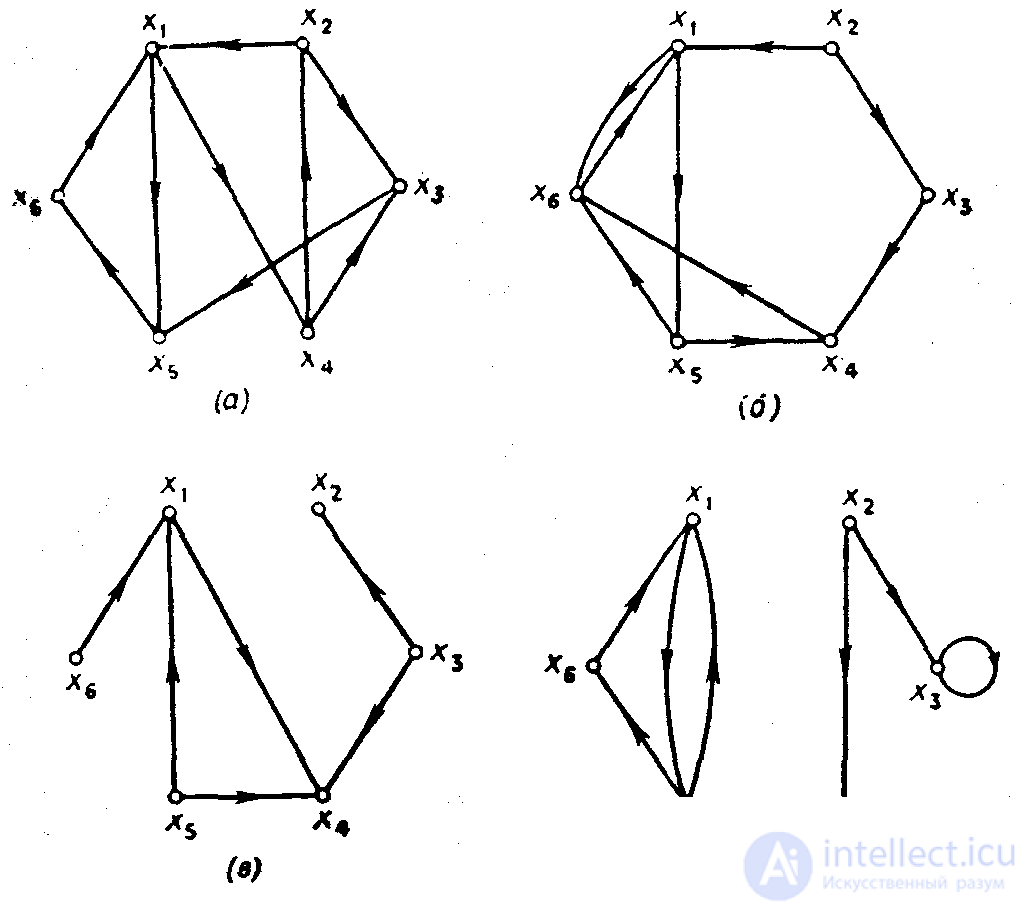
Рис. 1.7. (а) Сильно связанный граф, (б) Односторон не связный граф , (в) Слабо связный граф, (г) Несвязный граф.
Например, в графе G, приведенном на рис. 1.7(6), подграф 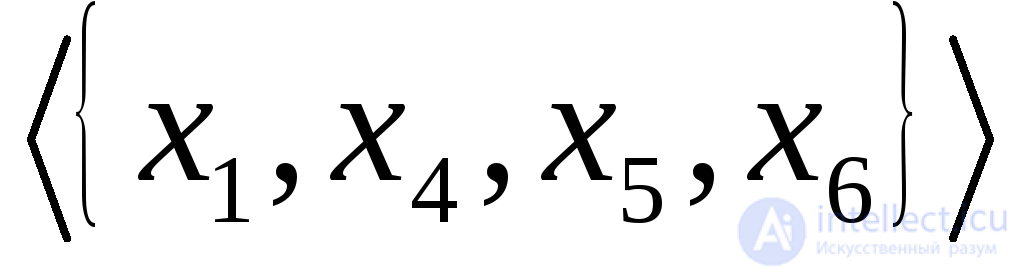 является сильной компонентой графаG. С другой стороны, подграфы
является сильной компонентой графаG. С другой стороны, подграфы 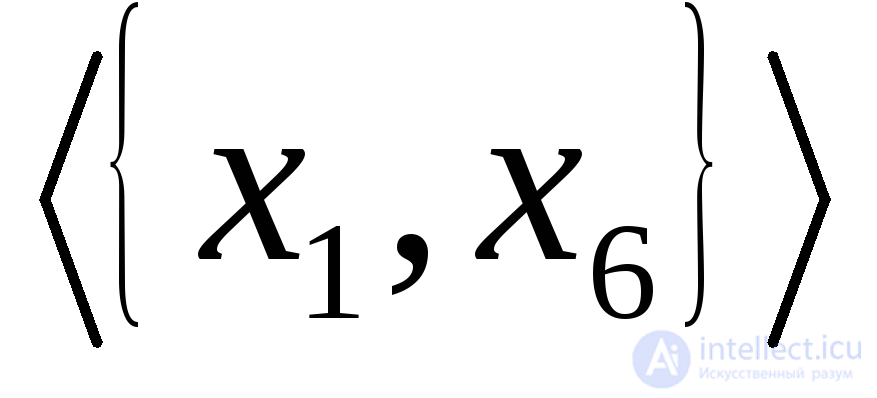 и
и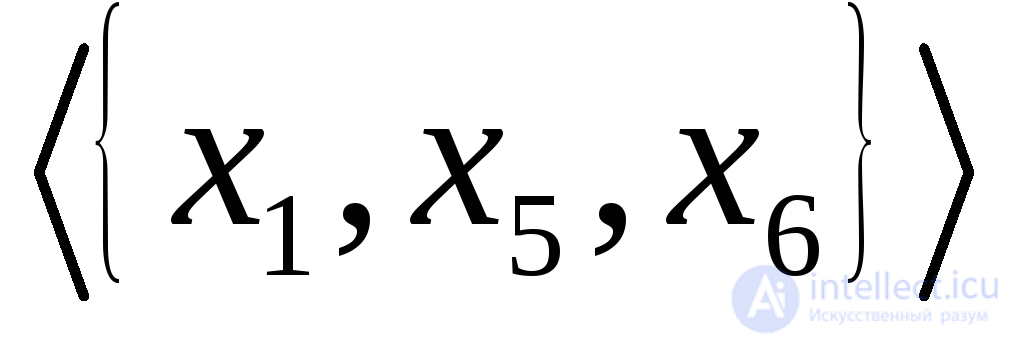 не являются сильными компонентами (хотя и являются сильными подграфами), поскольку они содержатся в графе
не являются сильными компонентами (хотя и являются сильными подграфами), поскольку они содержатся в графе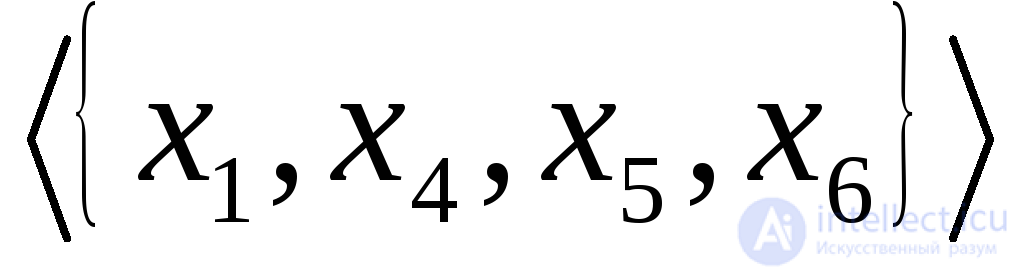 и, следовательно, не максимальные. В графе, показанном на рис. 1.7(в). подграф
и, следовательно, не максимальные. В графе, показанном на рис. 1.7(в). подграф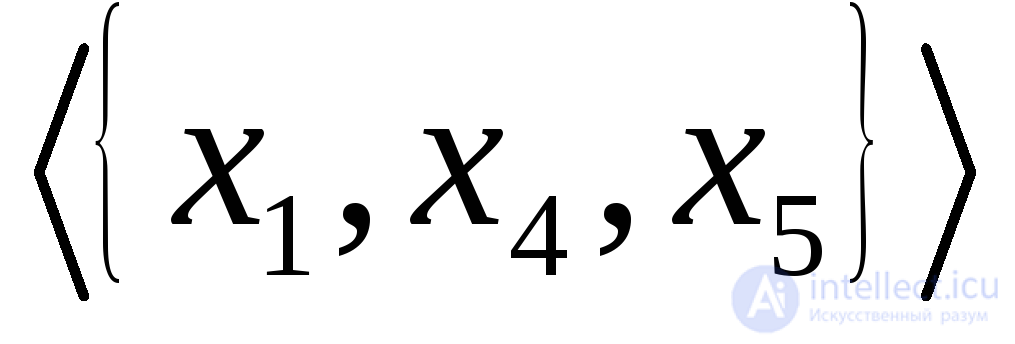 является односторонней компонентой. В графе, приведенном на рис. 1.7(г), оба подграфа
является односторонней компонентой. В графе, приведенном на рис. 1.7(г), оба подграфа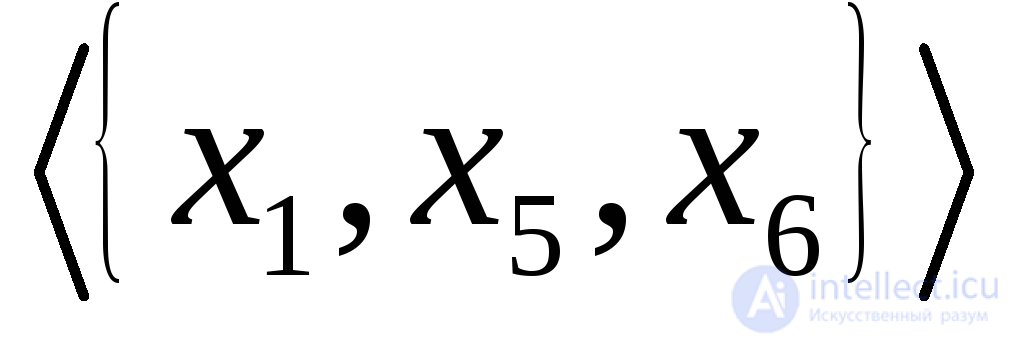 и
и 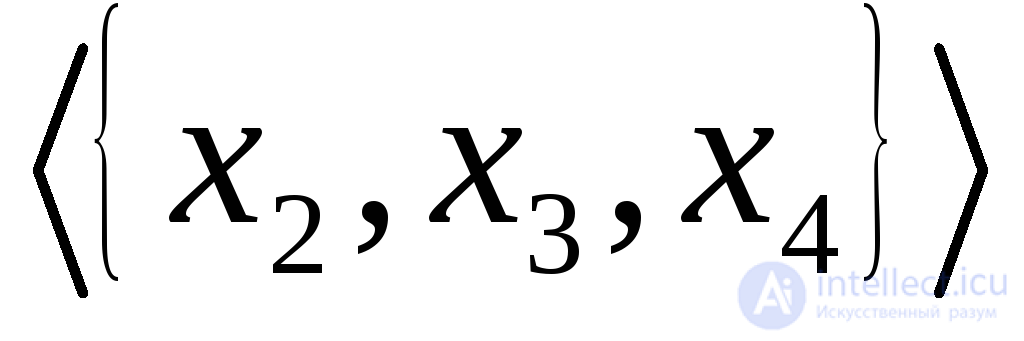 являются слабыми компонентами, и у этого графа только две такие компоненты.
являются слабыми компонентами, и у этого графа только две такие компоненты.
Из определений сразу же следует, что односторонние компоненты графа могут иметь общие вершины. Сильная компонента должна содержаться по крайней мере в одной односторонней компоненте, а односторонняя компонента содержится в некоторой слабой компоненте данного графа G.
1 Докажите, что если в графе от некоторой вершины существует маршрут до любой другой, то граф связен.
2 Докажите, что если в графе между некоторыми двумя вершинами существует маршрут, то существует также и путь, соединяющий эти две вершины.
3 В государстве 50 городов, причем от каждого города можно доехать до любого другого, возможно с пересадками. Какое наименьшее число дорог может быть в этом государстве?
4 На плоскости нарисованы вершины графа, пронумерованные числами от 2 до 30. При этом две вершины с номерами a и b соединены ребром только в том случае, если одно из чисел a или b делится на другое. Сколько компонент связности имеет этот граф?
5. Летом Иван отдыхал в молодежном лагере «Восход», где вместе с ним находилось всего 53 школьника. После окончания отдыха некоторые пары обменялись адресами, причем у каждого из отдыхающих оказалось не менее 26 адресов. Через некоторое время Ивану понадобился адрес Николая, с которым он адресом не обменивался. Докажите, что Иван может узнать адрес Николая, т.е. существует цепочка из школьников, которая начинается с Ивана и оканчивается Николаем и в которой каждая пара соседей обменялась адресами.
6. Степень каждой вершины связного графа – не менее 100. Одно ребро выкинули. Может ли получиться несвязный граф?
7. В локальной компьютерной сети от сервера отходит 21 провод, от остальных компьютеров – по 4 провода, а от принтера – один провод. Докажите, что с сервера можно послать документ на принтер.
8. В стране из каждого города выходит 100 дорог и от любого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь от любого города можно добраться до любого другого.
9. На конференции присутствуют 50 ученых, каждый из которых знаком по крайней мере с 25 участниками конференции. Докажите, что найдутся четверо из них, которых можно усадить за круглый стол так, чтобы каждый сидел рядом со знакомыми ему людьми.
10. В стране любые два города соединены или железной дорогой, или авиалинией. Доказать, что один из видов транспорта позволяет добраться из любого города в любой.
11. На листе бумаги отмечено 2011 точек. Двое играют в следующую игру: каждый своим ходом соединяет две отмеченные точки линией. Запрещается соединять пару точек повторно. Проигрывает тот, после хода которого из любой точки можно пройти в любую другую, двигаясь от вершины к вершине по проведенным линиям. Кто выигрывает при правильной игре?
12. В стране, кроме столицы, больше 100 городов. Столица страны соединена авиалиниями со 100 городами. Каждый из остальных городов соединен авиалиниями ровно с 10 городами. Известно, что из любого города можно перелететь в любой другой (может быть, с пересадками). В связи с экономическим кризисом было принято решение закрыть половину дорог из столицы. Докажите, что это можно сделать таким образом, чтобы после этого снова можно было бы из любого города перелететь в любой другой.
13. В стране 15 городов, некоторые из них соединены авиалиниями, принадлежащими трем авиакомпаниям. Известно, что даже если любая из авиакомпаний прекратитполеты, можно будет добраться из любого города в любой другой (возможно, с пересадками), пользуясь рейсами оставшихся двух компаний. Какое наименьшее количество авиалиний может быть в стране?
14. Между некоторыми из 2n городов установлено воздушное сообщение, причем каждый город связан (беспосадочными рейсами) не менее чем с n другими. Докажите, что если отменить любые n − 1 рейсов, то все равно из любого города можно добраться в любой другой на самолетах (с пересадками).
15. В некотором государстве города соединены дорогами. Длина любой дороги меньше 500 км, и из любого города в любой другой можно попасть, проехав по дорогам меньше 500 км. Когда одна дорога оказалась закрытой на ремонт, выяснилось, что из каждого города можно проехать по оставшимся дорогам в любой другой. Доказать, что при этом можно проехать меньше 1500 км.
16. Какое наименьшее число соединений требуется для организации проводной сети связи из 10 узлов, чтобы при выходе из строя любых двух узлов связи сохранялась возможность передачи информации между любыми двумя оставшимися (хотя бы по цепочке через другие узлы)?
17. На турбазе 12 домиков, между которыми крот прокопал 56 непересекающихся подземных ходов (два домика соединяются не более чем одним ходом). Докажите, что крот из любого домика может попасть в любой другой, передвигаясь по этим ходам.
18. Докажите, что граф на n вершинах, имеющий более (n − 1)(n − 2)/2 ребер, связный.
19. Каждая пара депутатов парламента либо дружит, либо враждует, причем имеется хотя бы одна пара враждующих депутатов. При этом неукоснительно соблюдаются условия «друг моего друга — мой друг» и «друг моего врага — мой враг». Известно, что в парламенте 50 депутатов, и что каждый из них послал открытки всем своим друзьям из числа коллег.
а) Какое наименьшее число открыток могло быть послано?
б) А наибольшее?
20. Числом связности χ графа называется наименьшее число вершин, удаление которых (вместе с выходящими из них ребрами) приводит к несвязному или одновершинному графу. Числом реберной связности λ графа называется наименьшее число ребер, удаление которых приводит к несвязному графу. Данные величины показывают, насколько граф «прочен», как много вершин и ребер нужно из него удалить, чтобы он «распался» на части.
а) Приведите примеры графа, для которого χ = 2, λ = 3.
б) Докажите, что для любого связного графа выполняется соотношение χ ≤ λ ≤ δ, где δ — минимальная из степеней вершин графа.
На этом все! Теперь вы знаете все про связный граф, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое связный граф, не связный граф, сильносвязный граф и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.