Лекция
Привет, Вы узнаете о том , что такое постоянный электрический ток, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое постоянный электрический ток, сила тока, напряжение, эдс, закон ома , настоятельно рекомендую прочитать все из категории Переменный электрический ток. Электромагнитное поле.
|
Электрический ток — это упорядоченное движение заряженных частиц. За направление тока принимают направление движения положительных зарядов. |
Различают несколько видов электрического тока. Предположим. что имеется макроскопическое заряженное тело (например, шар), которое перемещается в пространстве. Так как вместе с телом будут перемещаться заряды, то возникает направленное движение зарядов, то есть электрический ток. Такой ток, связанный с движением макроскопических тел, называется конвекционным (переносным) током. Если внутри какого-то тела упорядоченно перемещается некоторое число заряженных частиц вследствие того, что в нем создается электрическое поле, то такой ток называется током проводимости. Для возникновения тока проводимости необходимо наличие свободных носителей заряда.
В проводниках часть валентных электронов не связана с определенными атомами и может свободно перемещаться по всему его объему. В отсутствие приложенного к проводнику электрического поля такие свободные электроны — электроны проводимости — движутся хаотично, часто сталкиваясь с ионами и атомами, и изменяя при этом энергию и направление своего движения. Через любое сечение проводника в одну сторону проходит столько же электронов, сколько и в противоположную. Поэтому результирующего переноса электронов через такое сечение нет, и электрический ток равен нулю. Если же к концам проводника приложить разность потенциалов, то под действием сил электрического поля свободные заряды в проводнике начнут двигаться из области большего потенциала в область меньшего — возникнет электрический ток. Исторически сложилось так, что за направление тока принимают направление движение положительных зарядов, которое соответствует их переходу от большего потенциала к меньшему.
Электрический ток характеризуется силой тока I (рис. 4.1).
|
Сила тока есть скалярная величина, численно равная заряду переносимому через поперечное сечение проводника в единицу времени
|

Рис. 4.1. Сила тока в проводнике
Согласно (4.1), сила тока в проводнике равна отношению заряда 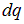 , прошедшего через поперечное сечение проводника за время
, прошедшего через поперечное сечение проводника за время  к этому времени.
к этому времени.
Замечание: В общем случае сила тока через некоторую поверхность равна потоку заряда через эту поверхность.
Если сила тока с течением времени не изменяется, то есть за любые равные промежутки времени через любое сечение проводника проходят одинаковые заряды, то такой ток называется постоянным, и тогда заряд, протекший за время t, может быть найден как (рис. 4.2)
|
|
(4.2) |
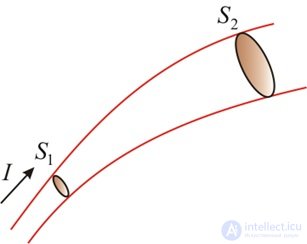
Рис. 4.2. Постоянный ток, протекающий через разные сечения проводника
|
Величина |
С учетом определения силы тока плотность тока через данное сечение  может быть выражена через силу тока
может быть выражена через силу тока  , протекающего через это сечение
, протекающего через это сечение
|
|
(4.3) |
При равномерном распределении потока зарядов по всей площади сечения проводника плотность тока равна
|
|
(4.4) |
|
В СИ единицей измерения силы тока является ампер (А). В СИ эта единица измерения является основной. |
Уравнение (4.1) связывает единицы измерения силы тока и заряда

|
В СИ единицей измерения плотности тока является ампер на квадратный метр (А/м2):
|
Это очень малая величина, поэтому на практике обычно имеют дело с более крупными единицами, например

Плотность тока можно выразить через объемную плотность зарядов  и скорость их движения v (рис. 4.3).
и скорость их движения v (рис. 4.3).

Рис. 4.3. К связи плотности тока j с объемной плотностью зарядов 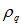 и дрейфовой скоростью v носителей заряда. За время dt через площадку S пройдут все заряды из объема dV = vdt S
и дрейфовой скоростью v носителей заряда. За время dt через площадку S пройдут все заряды из объема dV = vdt S
Полный заряд, проходящий за время dt через некоторую поверхность S, перпендикулярную вектору скорости v, равен
|
|
(4.5) |
Так как dq/(Sdt) есть модуль плотности тока j, можно записать
|
|
(4.6) |
Поскольку скорость v есть векторная величина, то и плотность тока также удобно считать векторной величиной, следовательно
|
|
|
|
Здесь  плотность заряда,
плотность заряда,  скорость направленного движения носителей заряда.
скорость направленного движения носителей заряда.
Замечание: Для общности использован индекс 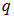 , так как носителями заряда, способными участвовать в создании тока проводимости, могут быть не только электроны, но, например, протоны в пучке, полученном из ускорителя или многозарядные ионы в плазме, или так называемые «дырки» в полупроводниках «р» типа, короче, любые заряженные частицы, способные перемещаться под воздействием внешних силовых полей.
, так как носителями заряда, способными участвовать в создании тока проводимости, могут быть не только электроны, но, например, протоны в пучке, полученном из ускорителя или многозарядные ионы в плазме, или так называемые «дырки» в полупроводниках «р» типа, короче, любые заряженные частицы, способные перемещаться под воздействием внешних силовых полей.
Кроме того, удобно выразить плотность заряда  через число
через число  носителей заряда в единице объема — (концентрацию носителей заряда)
носителей заряда в единице объема — (концентрацию носителей заряда)  . В итоге получаем:
. В итоге получаем:
|
|
(4.7) |
Следует подчеркнуть, что плотность тока, в отличие от силы тока — дифференциальная векторная величина. Зная плотность тока, мы знаем распределение течения заряда по проводнику. Силу тока всегда можно вычислить по его плотности. Соотношение (4.4) может быть «обращено»: если взять бесконечно малый элемент площади  , то сила тока через него определится как
, то сила тока через него определится как 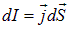 . Соответственно, силу тока через любую поверхность S можно найти интегрированием
. Соответственно, силу тока через любую поверхность S можно найти интегрированием
|
|
(4.8) |
Что же понимать под скоростью заряда v, если таких зарядов — множество, и они заведомо не движутся все одинаково? В отсутствие внешнего электрического поля, скорости теплового движения носителей тока 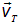 распределены хаотично, подчиняясь общим закономерностям статистической физики. Среднее статистическое значение
распределены хаотично, подчиняясь общим закономерностям статистической физики. Среднее статистическое значение  ввиду изотропии распределения по направлениям теплового движения. При наложении поля возникает некоторая дрейфовая скорость — средняя скорость направленного движения носителей заряда:
ввиду изотропии распределения по направлениям теплового движения. При наложении поля возникает некоторая дрейфовая скорость — средняя скорость направленного движения носителей заряда:
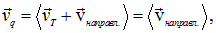
которая будет отлична от нуля. Проведем аналогию. Когда вода вырывается из шланга, и мы интересуемся, какое ее количество поступает в единицу времени на клумбу, нам надо знать скорость струи и поперечное сечение шланга. И нас совершенно не волнуют скорости отдельных молекул, хотя они и очень велики, намного больше скорости струи воды, как мы убедились в предыдущей части курса.
Таким образом, скорость 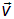 в выражении (4.7) — это дрейфовая скорость носителей тока в присутствии внешнего электрического поля или любого другого силового поля, обуславливающего направленное (упорядоченное) движение носители заряда. Если в веществе возможно движение зарядов разного знака, то полная плотность тока определяется векторной суммой плотностей потоков заряда каждого знака.
в выражении (4.7) — это дрейфовая скорость носителей тока в присутствии внешнего электрического поля или любого другого силового поля, обуславливающего направленное (упорядоченное) движение носители заряда. Если в веществе возможно движение зарядов разного знака, то полная плотность тока определяется векторной суммой плотностей потоков заряда каждого знака.
Как уже указывалось, в отсутствие электрического поля движение носителей заряда хаотично и не создает результирующего тока. Если, приложив электрическое поле, сообщить носителям заряда даже малую (по сравнению с их тепловой скоростью) скорость дрейфа, то, из-за наличия в проводниках огромного количества свободных электронов, возникнет значительный ток.
Поскольку дрейфовая скорость носителей тока создается электрическим полем, логично предположить пропорциональность
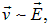
так что и плотность тока будет пропорциональна вектору напряженности (рис. 4.4)
|
|
(4.9) |
Более подробно этот вопрос обсуждается в Дополнении
Входящий в соотношение (4.9)
|
Коэффициент пропорциональности |
Проводимость связывает напряженность поля в данной точке с установившейся скоростью «течения» носителей заряда. Поэтому она может зависеть от локальных свойств проводника вблизи этой точки (то есть от строения вещества), но не зависит от формы и размеров проводника в целом. Соотношение (4.9) носит название закона Ома для плотности тока в проводнике (его называют также законом Ома в дифференциальной форме).
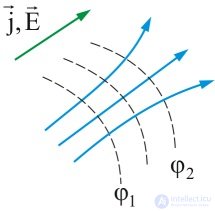
Рис. 4.4. Силовые линии электрического поля совпадают с линиями тока
Чтобы понять порядки величин, оценим дрейфовую скорость носителей заряда в одном из наиболее распространенных материалов — меди. Возьмем для примера силу тока I = 1 А, и пусть площадь поперечного сечения провода составляет
1 мм2 = 10–6 м2. Тогда плотность тока равна j = 106 А/м2. Теперь воспользуемся соотношением (4.7)

Носителями зарядов в меди являются электроны (е = 1.6·10-19 Кл), и нам осталось оценить их концентрацию  . В таблице Менделеева медь помещается в первой группе элементов, у нее один валентный электрон, который может быть отдан в зону проводимости. Поэтому число свободных электронов примерно совпадает с числом атомов. Берем из справочника плотность меди — r Cu=8,9·103 кг/м3. Молярная масса меди указана в таблице Менделеева — MCu = 63,5·10–3 кг/моль. Отношение
. В таблице Менделеева медь помещается в первой группе элементов, у нее один валентный электрон, который может быть отдан в зону проводимости. Поэтому число свободных электронов примерно совпадает с числом атомов. Берем из справочника плотность меди — r Cu=8,9·103 кг/м3. Молярная масса меди указана в таблице Менделеева — MCu = 63,5·10–3 кг/моль. Отношение
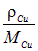
— это число молей в 1 м3. Умножая на число Авогадро Na = 6,02·1023 моль–1, получаем число атомов в единице объема, то есть концентрацию электронов
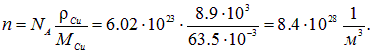
Теперь получаем искомую оценку дрейфовой скорости электронов
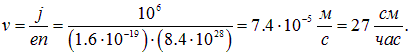
Для сравнения: скорости хаотического теплового движения электронов при 20°С в меди по порядку величины составляют 106 м/с, то есть на одиннадцать порядков величины больше.
Возьмем произвольную воображаемую замкнутую поверхность S, которую в разных направлениях пересекают движущиеся заряды. Мы видели, что полный ток через поверхность равен

где dq — заряд, пересекающий поверхность за время dt. Обозначим через q ' заряд, находящийся внутри поверхности. Его можно выразить через плотность заряда  , проинтегрированную по всему объему, ограниченному поверхностью
, проинтегрированную по всему объему, ограниченному поверхностью 

Из фундаментального закона природы - закона сохранения заряда — следует, что заряд dq, вышедший через поверхность за время dt, уменьшит заряд q ' внутри поверхности точно на эту же величину, то есть dq ' = –dq или
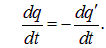
Подставляя сюда написанные выше выражения для скоростей изменения заряда внутри поверхности  , получаем математическое соотношение, выражающее закон сохранения заряда в интегральной форме
, получаем математическое соотношение, выражающее закон сохранения заряда в интегральной форме
|
|
(4.10) |
Напомним, что интегрирования ведутся по произвольной поверхности S и ограниченному ею объему V.
Пусть на концах проводника длиной l создана разность потенциалов  которая порождает внутри него электрическое поле Е, направленное в сторону падения потенциала (рис. 4.5-1). Если поле внутри проводника можно считать однородным, то
которая порождает внутри него электрическое поле Е, направленное в сторону падения потенциала (рис. 4.5-1). Если поле внутри проводника можно считать однородным, то
|
|
(4.11) |
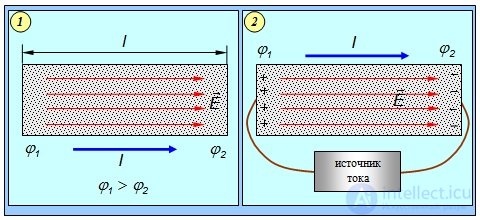
Рис. 4.5. Для возникновения тока необходима разность потенциалов на концах проводника.
Для поддержания разности потенциалов нужен источник тока
При этом в проводнике возникает электрический ток, который идет от большего потенциала  к меньшему
к меньшему 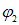 . Движение (положительных) зарядов от
. Движение (положительных) зарядов от  к
к  приводит к выравниванию потенциалов во всех точках. Электрическое поле в проводнике при этом исчезает, и ток прекращается. Очевидно, обязательным условием существования тока является наличие разности потенциалов
приводит к выравниванию потенциалов во всех точках. Электрическое поле в проводнике при этом исчезает, и ток прекращается. Очевидно, обязательным условием существования тока является наличие разности потенциалов

а для ее поддержания необходимо иметь специальное устройство, с помощью которого будет происходить разделение зарядов на концах проводника. Такое устройство называется источником тока. Таким образом, для получения тока требуется наличие замкнутой цепи и источника тока (рис. 4.5-2). Гальванические элементы, аккумуляторы, термоэлементы, электрические генераторы — примеры источников тока. Источник тока выполняет одновременно и вторую задачу — он замыкает электрическую цепь, по которой можно было бы осуществить непрерывное движение зарядов. Ток течет по внешней части — проводнику и по внутренней — источнику тока. Источник тока имеет два полюса: положительный, с более высоким потенциалом, и отрицательный, с более низким потенциалом. При разомкнутой внешней цепи на отрицательном полюсе источника тока образуется избыток электронов, а на положительном — недостаток. Разделение зарядов в источнике тока производится с помощью внешних, так называемых сторонних сил, направленных против электрических сил, действующих на разноименные заряды в проводниках самого источника тока. Природа сторонних сил может быть самой различной: механической, химической (рис. 4.6), тепловой, биологической и т. д.

Рис. 4.6. Действие сторонних сил химического происхождения
Итак, перемещение заряда по замкнутому проводнику под действием источника тока происходит за счет сил не электростатического происхождения — сторонних сил, действующих внутри источника. Электростатические силы не могут обеспечить движение зарядов по замкнутому контуру в силу своей консервативности (работа этих сил по замкнутому контуру равна нулю).
Таким образом, если цепь, состоящая из проводника и источника тока, замкнута, то по ней проходит ток, и при этом совершается работа сторонних сил. Эта работа складывается из работы, совершаемой против сил электрического поля внутри источника тока  , и работы, совершаемой против механических сил сопротивления среды источника
, и работы, совершаемой против механических сил сопротивления среды источника  , то есть
, то есть
|
|
(4.12) |
|
Отношение работы, которую совершают сторонние силы при перемещении точечного заряда вдоль всей цепи, включая и источник тока, к заряду, называется электродвижущей силой (ЭДС) источника тока:
|
Работа против сил электрического поля равна
|
|
(4.14) |
Если полюсы источника разомкнуты, то 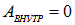 , и тогда
, и тогда
|
|
(4.15) |
то есть ЭДС источника тока при разомкнутой внешней цепи равна разности потенциалов, которая создается на его полюсах.
Распределение потенциала в замкнутой цепи представлено на рис. 4.7.

Рис. 4.7. Распределение потенциала в замкнутой электрической цепи
Ясно, что движение положительных зарядов происходит в сторону уменьшения потенциала. В то же время необходимо наличие области, где движение зарядов происходит в сторону увеличения потенциала за счет сторонних сил. Проще говоря: чтобы вода текла вниз, кто-то должен поднять ее наверх.
Выше отмечалось (см. (4.6)), что плотность тока j пропорциональна величине электрического поля Е
|
|
|
(4.6) |
Почему же мы приняли, что в проводниках средняя скорость зарядов постоянна и пропорциональна величине напряженности электрического поля, а не возрастает неограниченно? Действительно, свободные заряды вне проводника под действием однородного внешнего поля получали бы ускорение
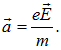
Таким образом, направленная скорость зарядов вдоль поля (или против поля, если заряды отрицательные) возрастала бы со временем. Тогда и плотность тока также росла бы со временем: j =
продолжение следует...
Часть 1 Постоянный электрический ток Сила тока, напряжение ,ЭДС, законы и правила
Часть 2 4.4. Зарядка конденсатора - Постоянный электрический ток Сила тока, напряжение
Часть 3 4.5. Правила Кирхгофа - Постоянный электрический ток Сила тока, напряжение
Часть 4 4.7. Классическая теория - Постоянный электрический ток Сила тока, напряжение
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика