Лекция
Привет, мой друг, тебе интересно узнать все про последовательное соединение, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое последовательное соединение, цепь rlc, режимы работы rlc-цепи , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства.
Последовательное соединения в электротехнике — это один из двух основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.
При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
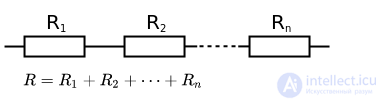
При последовательном соединении проводников сила тока в любых частях цепи одна и та же: (так как сила тока определяется количеством электронов, проходящих через поперечное сечение проводника, и если в цепи нет узлов, то все электроны в ней будут течь по одному проводнику).
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника питания, равно сумме напряжений на отдельных участках цепи: .
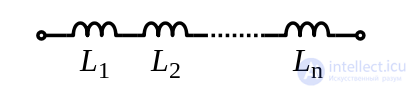
.

Цепь замкнута, когда замкнуты все выключатели. Цепь разомкнута, когда разомкнут хотя бы один выключатель. (аналог Логическая операция И)
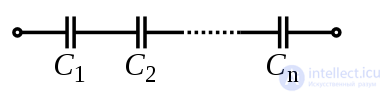
Цепь RLC - это электрическая цепь , состоящая из резистора (R), катушки индуктивности (L) и конденсатор (C), подключенный последовательно или параллельно. Название схемы образовано из букв, которые используются для обозначения составляющих компонентов этой схемы, причем последовательность компонентов может отличаться от RLC.
Схема формирует гармонический осциллятор для тока, а резонирует аналогично схеме LC . Добавление резистора увеличивает затухание этих колебаний, которое также известно как затухание . Резистор также снижает пиковую резонансную частоту. В обычных условиях некоторое сопротивление неизбежно, даже если резистор специально не включен в качестве компонента; идеальная, чистая LC-цепь существует только в области сверхпроводимости , физический эффект демонстрируется до сих пор только при температурах намного ниже температуры окружающей среды, наблюдаемой где-либо на поверхности Земли.
Цепи RLC имеют множество применений как схемы генератора . Радиоприемники и телевизоры используют их для настройки для выбора узкого диапазона частот от окружающих радиоволн. В этой роли схему часто называют настроенной схемой. Схема RLC может использоваться как полосовой фильтр , полосовой фильтр , фильтр нижних частот или фильтр верхних частот <358.>. Приложение настройки, например, является примером полосовой фильтрации. Фильтр RLC описывается как схема второго порядка, что означает, что любое напряжение или ток в цепи может быть описано с помощью дифференциального уравнения второго порядка в анализе схемы.
Три элемента схемы, R, L и C, могут быть объединены в несколько различных топологий . Все три последовательных элемента или все три параллельных элемента являются наиболее простыми по концепции и наиболее простыми для анализа. Однако есть и другие устройства, некоторые из которых имеют практическое значение в реальных схемах. Одна из часто встречающихся проблем - это необходимость учитывать сопротивление индуктора. Катушки индуктивности обычно состоят из катушек с проволокой, сопротивление которой обычно нежелательно, но часто оказывает значительное влияние на цепь.Википедия site:livepcwiki.ru
Последовательным соединением участков электрической цепи называют соединение, при котором через все участки проходит один ток (рис.3.5).
Напряжение на каждом последовательно включенном участке пропорционально величине сопротивления этого участка.
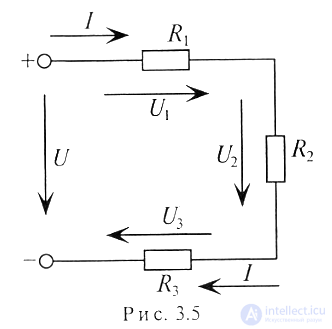
При последовательном соединении потребителей с сопротивлениями R1, R2 и R3 (рис. 3.5) напряжение на их зажимах равно
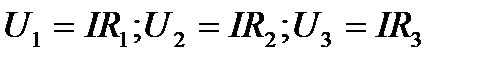
Воспользовавшись вторым законом Кирхгофа для рассматриваемой цепи (рис. 3.5), можно записать
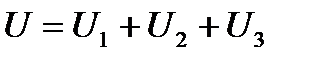 или
или 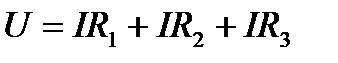 (1.28)
(1.28)
Откуда 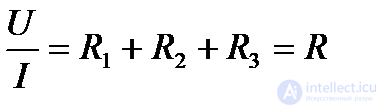 (1.29)
(1.29)
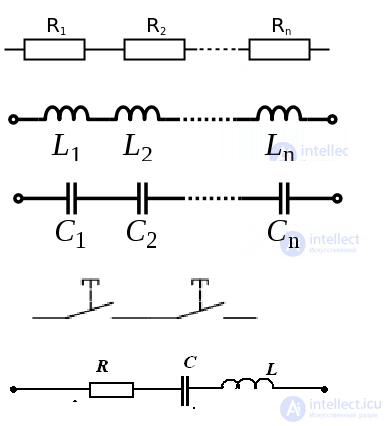
Таким образом, общее (эквивалентное) сопротивление R последовательно включенных сопротивлений (потребителей) равно сумме этих сопротивлений.
Ток в цепи последовательно включенных потребителей (рис. 3.5) определяется выражением
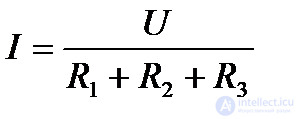
Нетрудно понять, что при изменении сопротивления хотя бы одного потребителя изменяется ток цепи, а следовательно, и режим работы (напряжение) всех последовательно включенных потребителей.
Поэтому последовательное соединение сопротивлений не нашло широкого практического применения.
Следует заметить, что при последовательном соединении резисторов на большем сопротивлении тратится большая мощность
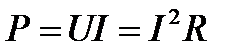

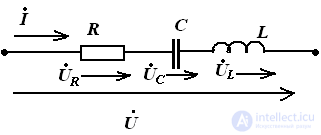
По второму закону Кирхгофа в комплексной форме
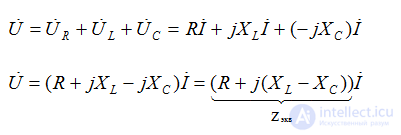
закон Ома
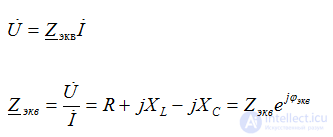
Zэкв – модуль эквивалентного сопротивления (полное сопротивление определяет связь между U и I)
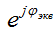 - аргумент, связь между начальными фазами
- аргумент, связь между начальными фазами 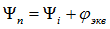
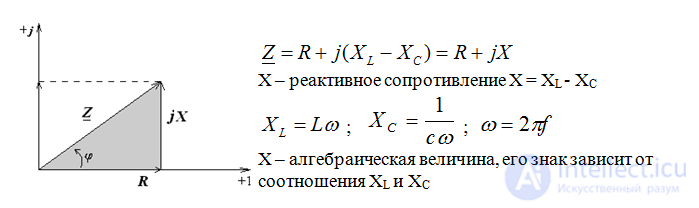
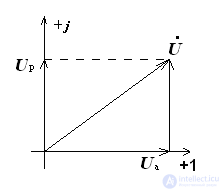
Из треугольника:

Треугольник напряжений
Онлайн демонстрация и симуляция работы Цепь RLC:
Открыть на весь экран Цепь RLC
Резонанс в цепи с последовательным соединением элементов. (Резонанс напряжений). (Рис. 63).
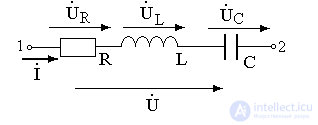
Рис. 63.
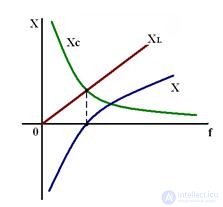
Режим работы RLC цепи или LC-цепи, при условии равенства реактивных сопротивлений XC = XL, когда общее напряжение цепи совпадает по фазе с ее током 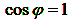 , называется резонансом напряжения.
, называется резонансом напряжения.
XC = XL – условие резонанса
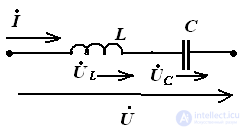
RLC цепь LC цепь.
Признаки резонанса напряжения:
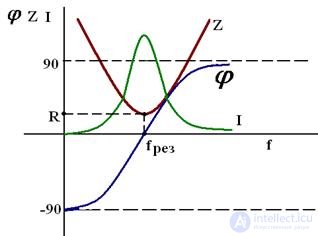
1. Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I и U φ = 0, cos φ = 1
2. Ток в цепи будет наибольшим и как следствие Pmax = I2maxR тоже максимальна, а реактивная мощность равна нулю.
3. Резонансная частота 
4. 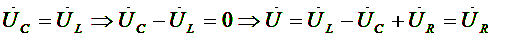
Резонанс можно достигнуть, изменяя L, C или ω.
Векторные диаграммы при резонансе напряжений
LC цепь RLC цепь
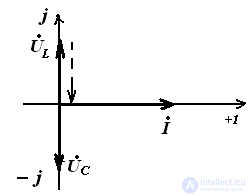
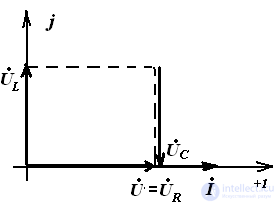
Резонанс в цепи с параллельным соединением элементов. (Резонанс токов). (Рис. 64).

Рис. 64.
Резонанс в цепи с параллельным соединением реальных элементов, т.е. резонанс с учетом потерь в активных сопротивлениях катушки и соединительных проводов. (Рис. 65).
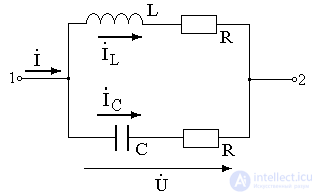
Рис. 65.
Эти режимы работы имеют важное практическое значение и обязательны для изучения.
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
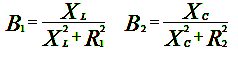
Условие резонанса токов: 
В1 – реактивная проводимость первой ветви,
В2 – реактивная проводимость второй ветви
Признаки резонанса токов:
 совпадают по фазе
совпадают по фазеRLC – цепь Векторная диаграмма
|
|
|
|
LC – цепь Векторная диаграмма
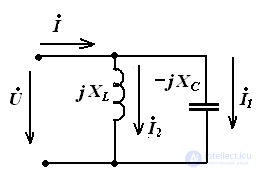

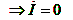
Резонансная частота
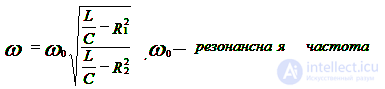
Случаи резонансных цепей цепей
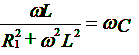
Если R2=0 резонанс наступит, при 
Случаи резонанса токов
Случай 1. Один резонанс в цепи, при условии:
Случай 2. Два резонанса в цепи, при определенном соотношении сопротивлений элементов 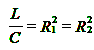
Случай 3. Нет резонанса в цепи – частота является величиной неопределенной, при
Частотные характеристики колебательного контура
Баланс мощностей в цепях переменного тока
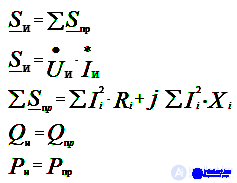
Коэффициент мощности
С уменьшением коэффициента мощности стоимость потребляемой электроэнергии возрастает .
Способы увеличения коэффициента мощности
Критический режим в последовательной RLC-цепи (критический случай апериодического режима) наблюдается, когда корни характеристического полинома последовательной RLC-цепи являются кратными
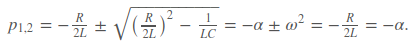
При этом (согласно уравнению состояния последовательной RLC-цепи, подключенной к источнику напряжения u0 = const) решение

действительно не содержит колебательной составляющей (как и при рассмотрении апериодического режима).
При начальных условиях
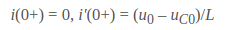
получим А1 = 0, следовательно,
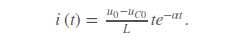
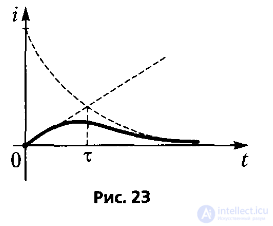
График критического процесса приведен на рис. Об этом говорит сайт https://intellect.icu . 23 (где линейная функция и экспонента намечены штриховыми линиями; периодическая составляющая в графике отсутствует, а максимум соответствует постоянной времени τ = 1/α).
Важным свойством этой схемы является ее способность резонировать на определенной частоте, резонансной частоте . y , f 0 . Частоты измеряются в единицах герц . В этой статье используется угловая частота , ω 0 , поскольку это более удобно с математической точки зрения. Измеряется в радианах в секунду. Они связаны друг с другом простой пропорцией,
Резонанс возникает, потому что энергия для этой ситуации сохраняется двумя разными способами: в электрическом поле, когда конденсатор заряжается и в магнитном поле, когда ток течет через индуктор. Энергия может передаваться от одного к другому в цепи, и это может быть колебательным. Механическая аналогия - это груз, подвешенный на пружине, которая при отпускании будет колебаться вверх и вниз. Это не мимолетная метафора; Вес на пружине описывается точно таким же дифференциальным уравнением второго порядка, что и цепь RLC, и для всех свойств одной системы будет обнаружено аналогичное свойство другой. Механическое свойство, отвечающее резистору в цепи, - это трение в системе пружина-груз. Трение будет медленно останавливать любое колебание, если его не движет внешняя сила. Точно так же сопротивление в цепи RLC будет «гасить» колебания, уменьшая их со временем, если в цепи нет источника питания переменного тока.
Резонансная частота определяется как частота, на которой импеданс контура минимален. Эквивалентно, его можно определить как частоту, на которой импеданс является чисто реальным (то есть чисто резистивным). Это происходит потому, что импедансы катушки индуктивности и конденсатора в резонансе равны, но имеют противоположный знак и компенсируются. Цепи, в которых L и C подключены параллельно, а не последовательно, на самом деле имеют максимальный импеданс, а не минимальный. По этой причине их часто называют антирезонаторами , однако по-прежнему принято называть частоту, на которой это происходит, резонансной частотой.
Резонансная частота определяется в терминах импеданса, подаваемого на источник возбуждения. Схема все еще может продолжать колебаться (в течение некоторого времени) после того, как источник возбуждения был удален или она подвергается скачку напряжения (включая скачок до нуля). Это похоже на то, как камертон продолжает звонить после удара, и этот эффект часто называют звоном. Этот эффект представляет собой пиковую собственную резонансную частоту контура и, как правило, не совсем то же самое, что и частота возбуждаемого резонанса, хотя они обычно довольно близки друг к другу. Разные авторы используют разные термины, чтобы различать эти два явления, но без определения резонансной частоты обычно означает возбуждаемую резонансную частоту. Возбужденная частота может называться незатухающей резонансной частотой или незатухающей собственной частотой, а пиковая частота может называться затухающей резонансной частотой или затухающей собственной частотой. Причина этой терминологии заключается в том, что возбуждаемая резонансная частота в последовательном или параллельном резонансном контуре имеет значение
Это в точности то же самое, что резонансная частота LC-контура, то есть без резистора. Резонансная частота для контура RLC такая же, как и для контура, в котором нет демпфирования, следовательно, резонансная частота незатухает. Пиковая резонансная частота, с другой стороны, зависит от номинала резистора и описывается как затухающая резонансная частота. Цепь с сильным демпфированием вообще не будет резонировать, если ее не использовать. Цепь со значением резистора, которое приводит к тому, что она находится на границе звона, называется с критическим демпфированием . Любая сторона критически затухающего сигнала описывается как недостаточное демпфирование (происходит звон) и сверхдемпфирование (звон подавляется).
Цепи с топологией более сложной, чем прямая последовательная или параллельная (некоторые примеры описаны далее в статье), имеют возбуждаемую резонансную частоту, которая отклоняется от , и для них незатухающая резонансная частота, затухающая резонансная частота и возбуждаемая резонансная частота могут быть разными.
Демпфирование вызвано сопротивлением в цепи. Он определяет, будет ли цепь резонировать естественным образом (то есть без источника возбуждения). Цепи, которые будут резонировать таким образом, описываются как недемпфированные, а те, которые не будут, - как чрезмерно демпфированные. Затухание демпфирования (символ α) измеряется в неперс в секунду. Однако безразмерный коэффициент затухания (символ ζ, дзета) часто является более полезной мерой, которая связана с α соотношением
Частный случай ζ = 1 называется критическим демпфированием и представляет случай схемы, которая просто на границе колебания. Это минимальное демпфирование, которое можно применить, не вызывая колебаний.
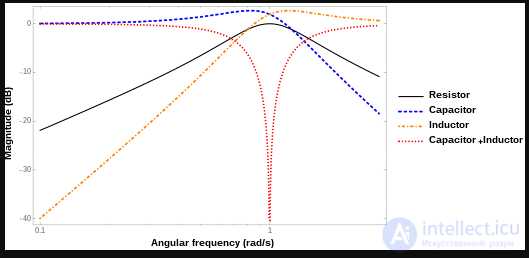
Эффект резонанса можно использовать для фильтрации, быстрое изменение импеданса вблизи резонанса может использоваться для пропускания или блокировки сигналов, близких к резонансной частоте. Могут быть сконструированы как полосовые, так и полосовые фильтры, некоторые схемы фильтров показаны ниже в статье. Ключевым параметром в конструкции фильтра является полоса пропускания . Полоса пропускания измеряется между частотами среза , наиболее часто определяемыми как частоты, на которых мощность, передаваемая через цепь, упала до половины значения, передаваемого при резонансе. Есть две из этих частот половинной мощности: одна выше и одна ниже резонансной частоты
где Δω - ширина полосы частот, ω 1 - нижняя частота половинной мощности, а ω 2 - верхняя частота половинной мощности. Полоса пропускания связана с ослаблением на
, где единицы измерения - радианы в секунду и неперс на второй соответственно. Для других единиц может потребоваться коэффициент пересчета. Более общая мера ширины полосы - это относительная ширина полосы, которая выражает ширину полосы как долю резонансной частоты и выражается как
Дробная пропускная способность также часто указывается в процентах. Демпфирование цепей фильтров регулируется для достижения требуемой полосы пропускания. Узкополосный фильтр, такой как режекторный фильтр , требует низкого демпфирования. Широкополосный фильтр требует сильного демпфирования.
Добротность - широко распространенная мера, используемая для характеристики резонаторов. Он определяется как пиковая энергия, запасенная в цепи, деленная на среднюю энергию, рассеиваемую в ней на радиан при резонансе. Следовательно, схемы с низкой добротностью демпфируются, а схемы с потерями и высокой добротности - недостаточно. Q относится к пропускной способности; Цепи с низкой добротностью являются широкополосными, а схемы с высокой добротностью - узкополосными. Фактически бывает, что Q является обратной величиной дробной ширины полосы
Q-фактор прямо пропорциональна избирательности , так как добротность обратно пропорциональна ширине полосы.
Для последовательного резонансного контура добротность можно вычислить следующим образом:
Параметры ζ, F b и Q масштабируются до ω 0 . Это означает, что схемы со схожими параметрами имеют одинаковые характеристики независимо от того, работают они в одной полосе частот или нет.
В следующей статье дается подробный анализ последовательной цепи RLC. Остальные конфигурации так подробно не описаны, но указаны основные отличия от серийного корпуса. Общая форма дифференциальных уравнений, приведенная в разделе последовательной схемы, применима ко всем схемам второго порядка и может использоваться для описания напряжения или тока в любом элементе каждой цепи.
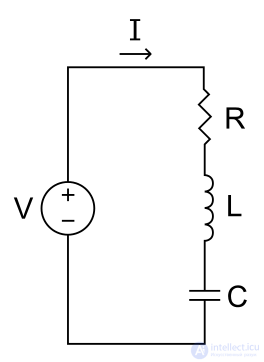
В этой схеме все три компонента включены последовательно с источником напряжения . Основное дифференциальное уравнение можно найти, подставив в закон напряжения Кирхгофа (KVL) определяющее уравнение для каждого из трех элементов. Из KVL
где V R , V L и V C - это напряжения на R, L и C соответственно, а V (t) - изменяющееся во времени напряжение от источника.
Подстановка ,
и
в уравнение выше дает:
Для случая, когда источником является неизменное напряжение, взятие производной по времени и деление на L приводит к следующему дифференциальному уравнению второго порядка:
Полезно выразить это в более общей форме:
α и ω 0 оба выражены в единицах угловой частоты . α называется непер частотой или затуханием и является мерой того, насколько быстро переходная характеристика схемы затухнет после устранения стимула. Непер встречается в названии, потому что единицы измерения можно также рассматривать как непер в секунду, где непер - это единица затухания. ω 0 - частота углового резонанса.
Для случая последовательной цепи RLC эти два параметра задаются следующим образом:
Полезный параметр - коэффициент затухания ζ, который определяется как отношение этих двух; хотя иногда α упоминается как коэффициент затухания, а ζ не используется.
В случае последовательной цепи RLC коэффициент демпфирования определяется как
Значение коэффициента демпфирования определяет тип переходного процесса,
Дифференциальное уравнение имеет характеристическое уравнение ,
Корни уравнения в s-области:
Общее решение дифференциального уравнения представляет собой экспоненту в корне или линейную суперпозицию обоих,
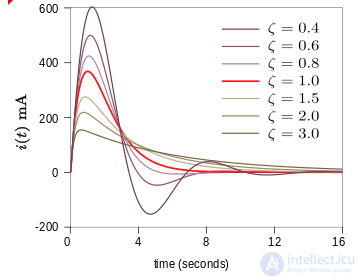
Коэффициенты A 1 и A 2 определяются граничными условиями конкретной анализируемой задачи. То есть они устанавливаются значениями токов и напряжений в цепи в начале переходного процесса и предполагаемым значением, на котором они установятся через бесконечное время. Дифференциальное уравнение для схемы решается тремя разными способами в зависимости от значения ζ. Это избыточное демпфирование (ζ>1), недостаточное демпфирование (ζ < 1), and critically damped (ζ = 1).
сверхдемпфирование (ζ>1):
Отклик с избыточным демпфированием - это затухание переходного тока без колебаний.
Отклик с недостаточным демпфированием (ζ < 1) is
Применяя стандартные тригонометрические тождества , две тригонометрические функции могут быть выражены как одна синусоида со сдвигом фазы,
Отклик с недостаточным демпфированием представляет собой затухающее колебание на частоте ω d . Колебание затухает со скоростью, определяемой затуханием α. Экспонента в α описывает огибающую колебания. B 1 и B 2 (или B 3 и фазовый сдвиг φ во второй форме) являются произвольными константами, определяемыми граничными условиями. Частота ω d определяется как
Это называется затухающей резонансной частотой или затухающей собственной частотой. Это частота, на которой цепь будет естественным образом колебаться, если не будет управляться внешним источником. Резонансная частота ω 0 , которая представляет собой частоту, на которой цепь будет резонировать под воздействием внешнего колебания, часто может называться незатухающей резонансной частотой, чтобы отличить ее.
Критически затухающий отклик (ζ = 1) равен
Критически затухающий отклик представляет отклик схемы, которая затухает в кратчайшие сроки, не допуская колебаний. Это соображение важно в системах управления, где требуется как можно быстрее достичь желаемого состояния без перескока. D 1 и D 2 - произвольные константы, определяемые граничными условиями.
Последовательный RLC может быть проанализирован как для переходных, так и для установившихся Поведение состояния переменного тока с использованием преобразования Лапласа . Если вышеупомянутый источник напряжения формирует сигнал с преобразованным по Лапласу V (s) (где s - комплексная частота s = σ + jω), KVL может применяться в Лапласе. домен:
где I (s) - ток, преобразованный по Лапласу во всех компонентах. Решение относительно I (s):
И переставляя, мы получаем
Решение для лапласовской проводимости Y (s):
Упрощая с использованием параметров α и ω 0 , определенных в предыдущем разделе, мы имеем
нули Y (s) - это такие значения s, что Y (s ) = 0:
полюса Y (s) - это значения s, такие что Y (s) → ∞. По квадратичной формуле находим
Полюса Y (s) идентичны корни s 1 и s 2 характеристического полинома дифференциального уравнения в разделе выше.
Для произвольного V (t) решение, полученное обратным преобразованием I (s), будет:
где ω r = √α - ω 0 , а ch и sinh - обычные гиперболические функции .
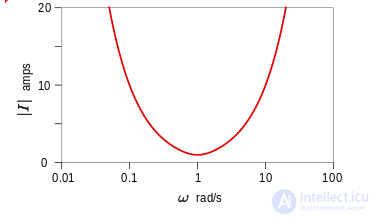
Синусоидальное установившееся состояние представлено положением s = jω, где j - мнимая единица . Принимая величину вышеуказанного уравнения с этой заменой:
, а ток как функцию от ω можно найти в
Имеется пиковое значение | I (jω) |. Величина ω на этом пике в данном конкретном случае равна незатухающей собственной резонансной частоте:
Из частотной характеристики тока, частотной характеристики напряжений на различных элементах схемы также можно определить.
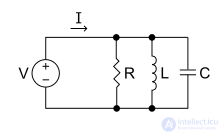
Свойства параллельной цепи RLC могут быть получены из отношения двойственности электрических цепей и учитывая, что параллельный RLC является двойным импедансом последовательного RLC. Принимая во внимание это, становится ясно, что дифференциальные уравнения, описывающие эту схему, идентичны общему виду уравнений, описывающих последовательный RLC.
Для параллельной схемы затухание α определяется как
и, следовательно, коэффициент демпфирования
Аналогично, другие масштабированные параметры, относительная полоса пропускания и Q также являются обратными друг другу. Это означает, что широкополосная схема с низкой добротностью в одной топологии станет узкополосной схемой с высокой добротностью в другой топологии, если будет построена из компонентов с одинаковыми значениями. Дробная полоса пропускания и Q параллельной схемы задаются как
Обратите внимание, что приведенные здесь формулы являются обратными значениям формул для ряда схема, приведенная выше.
Дается комплексная проводимость этой цепи путем сложения проводимости компонентов:
Результатом перехода от последовательного расположения к параллельному расположению в цепи, имеющей пик импеданса при резонансе, а не минимум, поэтому цепь является антирезонатором.
График напротив показывает, что существует минимум частотной характеристики тока на резонансной частоте , когда цепь приводится в действие постоянным напряжением. С другой стороны, при управлении постоянным током будет максимум напряжения, который будет следовать той же кривой, что и ток в последовательной цепи.
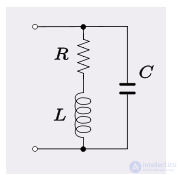
Последовательный резистор с катушкой индуктивности в параллельной LC-цепи, как показано на рисунке 4, представляет собой топологию, которая обычно встречается необходимо учитывать сопротивление обмотки катушки. Параллельные LC-цепи часто используются для полосовой фильтрации , и добротность в значительной степени определяется этим сопротивлением. Резонансная частота этого контура
Это резонансная частота цепи, определяемая как частота, на которой полная проводимость имеет нулевую мнимую часть. Частота, которая появляется в обобщенной форме характеристического уравнения (которое для этой схемы такое же, как и ранее)
- это не та же частота. В данном случае это естественная незатухающая резонансная частота:
Частота ω m , при которой величина импеданса максимальна, равна задается
где Q L = ω '0 L / R - коэффициент качества катушки. Это может быть хорошо аппроксимировано выражением
Кроме того, точное значение максимального импеданса определяется как
Для значений Q L больше единицы это может быть хорошо аппроксимировано выражением
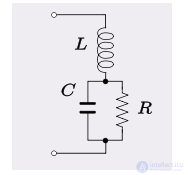
В том же ключе, резистор, включенный параллельно конденсатору в последовательной LC-цепи, можно использовать для обозначения конденсатора с диэлектриком с потерями. Эта конфигурация показана на рисунке 5. Резонансная частота (частота, при которой импеданс имеет нулевую мнимую часть) в этом случае определяется выражением
, а частота ω m , при котором величина импеданса минимальна, определяется как
где Q C = ω ′ 0 RC.
Первое свидетельство того, что конденсатор может производить электрические колебания, было обнаружено в 1826 году французским ученым Феликсом Савари . Он обнаружил, что когда лейденская банка разряжалась через проволоку, намотанную вокруг железной иглы, иногда игла оставалась намагниченной в одном направлении, а иногда в противоположном. Он правильно предположил, что это было вызвано затухающим колеблющимся током разряда в проводе, который менял намагниченность иглы назад и вперед до тех пор, пока она не становилась слишком маленькой, чтобы оказывать влияние, оставляя иглу намагниченной в случайном направлении.
Американский физик Джозеф Генри повторил эксперимент Савари в 1842 году и пришел к такому же выводу, очевидно независимо. Британский ученый Уильям Томсон (лорд Кельвин) в 1853 году математически показал, что разряд лейденской банки через индуктивность должен быть колебательным, и вывел его резонансную частоту.
Британский радиоисследователь Оливер Лодж , разрядив большую батарею лейденских банок через длинный провод, создал настроенный контур с его резонансной частотой в звуковом диапазоне, который создавал музыкальный тон из искры при ее разряде. В 1857 году немецкий физик Беренд Вильгельм Феддерсен сфотографировал искру, вызванную резонансным контуром лейденской банки во вращающемся зеркале, предоставив видимые свидетельства колебаний. В 1868 году шотландский физик Джеймс Клерк Максвелл вычислил эффект приложения переменного тока к цепи с индуктивностью и емкостью, показав, что отклик максимален на резонансной частоте.
Первый пример электрической резонансной кривой был опубликован в 1887 году немецким физиком Генрихом Герцем в его новаторской статье об открытии радиоволн, показывающей длину искры, получаемой от его искрового разрядника LC-резонатора детекторы как функция частоты.
Одной из первых демонстраций резонанса между настроенными схемами был эксперимент Лоджа с "синтонными сосудами" около 1889 года. Он поместил два резонансных контура рядом друг с другом, каждый из которых состоял из лейденского сосуда, подключенного к регулируемая одновитковая катушка с искровым разрядником. Когда высокое напряжение от индукционной катушки прикладывалось к одному настроенному контуру, создавая искры и, следовательно, колеблющиеся токи, искры возбуждались в другом настроенном контуре только тогда, когда индукторы были настроены на резонанс. Лодж и некоторые английские ученые предпочли термин «синтония» для этого эффекта, но термин «резонанс» в конце концов прижился.
Первое практическое использование RLC-схем было в 1890-х годах в радиопередатчиках с искровым разрядником. для настройки приемника на передатчик. Первый патент на радиосистему, позволяющую настройку, был подан Лоджем в 1897 году, хотя первые практические системы были изобретены в 1900 году англо-итальянским пионером радио Гульельмо Маркони .
Эти схемы очень часто используются в схемах настройки аналоговых радиоприемников. Регулируемая настройка обычно достигается с помощью параллельного пластинчатого переменного конденсатора , который позволяет изменять значение C и настраиваться на станции на разных частотах. Для каскада ПЧ в радиостанции, где настройка предустановлена на заводе, более обычным решением является регулируемый сердечник в катушке индуктивности для регулировки L. В этой конструкции сердечник (сделанный из высокого проницаемость материал, который имеет эффект увеличения индуктивности) имеет резьбу, так что его можно ввинтить или вывинтить из обмотки индуктора, если это необходимо.
|
|
|
|
|
|
В приложении фильтрации резистор становится нагрузкой, которую фильтр работая в. Значение коэффициента демпфирования выбирается исходя из желаемой полосы пропускания фильтра. Для более широкой полосы пропускания требуется большее значение коэффициента демпфирования (и наоборот). Эти три компонента дают дизайнеру три степени свободы. Два из них необходимы для установки полосы пропускания и резонансной частоты. У дизайнера остается один, который можно использовать для масштабирования R, L и C до удобных практических значений. В качестве альтернативы R может быть задано внешней схемой, которая будет использовать последнюю степень свободы.
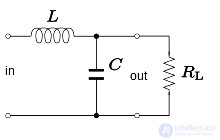
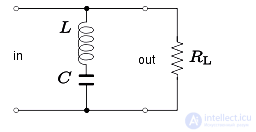
Схема RLC может использоваться как фильтр нижних частот. Конфигурация схемы показана на рисунке 6. Частота излома, то есть частота точки 3 дБ, задается как
Это также полоса пропускания фильтра. Коэффициент демпфирования определяется как
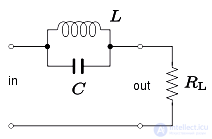
Фильтр верхних частот показан на рисунке 7. Частота излома такая же, как у фильтра нижних частот:
Фильтр имеет полосу заграждения этой ширины.
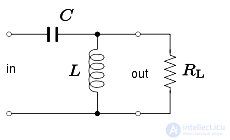
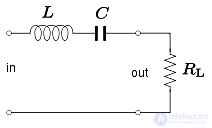
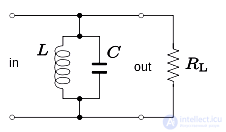
Полосовой фильтр может быть сформирован со схемой RLC путем размещения последовательной LC-цепи последовательно с нагрузочным резистором или путем размещения параллельной LC-цепи параллельно нагрузке. резистор. Эти устройства показаны на рисунках 8 и 9 соответственно. Центральная частота задается следующим образом:
и ширина полосы для последовательной цепи составляет
Шунтовая версия схемы предназначена для работы от источника с высоким импедансом, то есть постоянного Источник тока. В этих условиях ширина полосы составляет
На рисунке 10 показан полосовой фильтр, образованный серией LC-цепь шунтируется через нагрузку. На рисунке 11 показан полосовой фильтр, образованный параллельной LC-цепью, включенной последовательно с нагрузкой. Первый случай требует высокого Источник импеданса, так что ток отводится в резонатор, когда он становится низким в резонансе. Во втором случае требуется источник с низким импедансом, чтобы напряжение на антирезонаторе падало, когда он становится высоким при резонансе.
Для применений в схемах генераторов обычно желательно сделать затухание (или, что то же самое, коэффициент затухания) как можно меньше. На практике для достижения этой цели необходимо сделать сопротивление цепи R как можно меньшим физически для последовательной цепи или, в качестве альтернативы, увеличить R до максимально возможного значения для параллельной цепи. В любом случае RLC-схема становится хорошим приближением к идеальной LC-схеме . Однако для схем с очень низким затуханием (высокая добротность) могут стать важными такие вопросы, как диэлектрические потери катушек и конденсаторов.
В схеме генератора
или эквивалентно
В результате
В последовательной цепи RLC при резонансе ток ограничивается только сопротивление цепи
Если R мало, например, состоящее только из сопротивления обмотки индуктора, тогда этот ток будет большим. Это снизит напряжение на катушке индуктивности
Напряжение равной величины также будет наблюдаться на конденсаторе, но в противофазе к катушке индуктивности. Если R можно сделать достаточно малым, эти напряжения могут в несколько раз превышать входное напряжение. Фактически, коэффициент напряжения - это добротность схемы,
Аналогичный эффект наблюдается с токами в параллельной цепи. Несмотря на то, что внешнему источнику кажется, что цепь имеет высокий импеданс, во внутреннем контуре параллельной катушки индуктивности и конденсатора циркулирует большой ток.
В качестве цепи импульсного разряда может использоваться последовательная RLC-цепь с избыточным демпфированием. Часто бывает полезно знать значения компонентов, которые можно использовать для создания сигнала. Это описывается формой
Такой Схема может состоять из конденсатора накопления энергии, нагрузки в виде сопротивления, некоторой индуктивности цепи и переключателя - и все это последовательно. Начальные условия заключаются в том, что конденсатор находится под напряжением V 0 и в катушке индуктивности нет тока. Если индуктивность L известна, то остальные параметры задаются следующим образом - емкость:
сопротивление (сумма цепи и нагрузки):
начальное напряжение на клеммах конденсатора:
Перестановка для случая, когда R известно - емкость:
индуктивность (сумма цепи и нагрузки):
начальное напряжение на клеммах конденсатора:
Понравилась статья про последовательное соединение? Откомментируйте её Надеюсь, что теперь ты понял что такое последовательное соединение, цепь rlc, режимы работы rlc-цепи и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Электротехника, Схемотехника, Аналоговые устройства
Термины: Электротехника, Схемотехника, Аналоговые устройства