Лекция
Привет, сегодня поговорим про отношение порядка, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое отношение порядка , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
отношение порядка принято обозначать символом £. Запись Х£У означает, что пара (Х, у) принадлежит множеству АÌМ´М, являющемуся отношением порядка в М, причем Х предшествует У (или У следует за Х).
Отношение порядка обладает свойствами:
· Рефлексивности х £ Х;
· Транзитивности; Если Х £ У, а У £ Z , то Х £ Z;
· Антисимметричности; Если Х £ У, а У £ Х, то Х = У.
Множество, на котором определено отношение порядка, называется Упорядоченным, и говорят, что порядок введен этим отношением.
Если для любых двух элементов Х и У множества М имеет место отношение Х £ У (или У £ Х), то М –Совершенно (линейно) упорядоченно.
Например, множество натуральных или действительных чисел с естественным отношением порядка £ являются совершенно упорядоченными.
В общем случае может оказаться, что для некоторых пар (Х, у) ни одно из соотношений Х £ У и У £ Х не имеет места. Такие элементы называются Несравнимыми, а множество М называется Частично упорядоченным.
Примерами частичного порядка является отношение «быть делителем», отношение включения Ì и т. п. Так, отношение включения на множестве подмножеств МI некоторого универсума М рефлексивно (МI Ì МI), транзитивно (если МI Ì МJ, a МJ Ì МK, то МI Ì МK) и антисимметрично (из МI Ì МJ, и МJÌ МI следует МI = МJ), но среди всевозможных подмножеств имеются такие, что ни одно из соотношений из МI Ì МN, и МNÌ МI Не имеет места. Аналогично не все пары элементов из множества натуральных чисел находятся в отношении «быть делителем».
В заметке рассматривается одно из наиболее употребительных бинарных отношений - отношение порядка.
Порядок играет огромную роль в нашей жизни. Люди на протяжении всей истории пытались упорядочить отношения между собой, окружающие явления. Без порядка невозможно представить жизнь человека. Попробуйте представить общество, в котором царит анархия или словарь, в котором слова расположены хаотично. Но что такое порядок? С некоторыми упорядочениями мы настолько свыклись, что часто их просто не осознаем, как, например, грамматический порядок слов в предложении. В данной статье дано формальное определение порядка, которое используется в математике.
Определение 1.1. Бинарное отношение a на множестве X называется отношением порядка, если оно транзитивно:
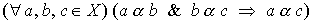
и антисимметрично:
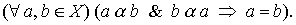
Пример 1.1. Рассмотрим отношение "старше" на множестве людей. Очевидно, что оно транзитивно и антисимметрично, и, следовательно, является отношением порядка.
Пример 1.2. Иерархия животных, построенная по этапам эволюции, является отношением порядка (рис.1).

Рис. 1. Основные этапы эволюции эукариотических организмов
Определение 1.2. Множество X с определенным на нем отношением порядка 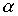 называется упорядоченным множеством и обозначается
называется упорядоченным множеством и обозначается  .
.
Упорядоченное множество 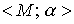 с небольшим числом элементов наглядно представляется ориентированным графом. При этом элементам множества M сопоставляются вершины графа (обозначаются на рисунке точками), а элементам отношения a - дуги (линии со стрелками).
с небольшим числом элементов наглядно представляется ориентированным графом. При этом элементам множества M сопоставляются вершины графа (обозначаются на рисунке точками), а элементам отношения a - дуги (линии со стрелками).
Так, например, на рисунке 2 приведен ориентированный граф, представляющий отношение 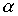 = {(a, a), (a, b), (a, c), (b, c)} на множестве M = {a, b, c, d}.
= {(a, a), (a, b), (a, c), (b, c)} на множестве M = {a, b, c, d}.
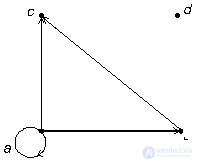
Рис. 2. Граф упорядоченного множества
Задать порядок на множестве можно различными способами. Так, например, на рисунке 3 приведено три способа упорядочения четырех стран.
| Площадь | Россия | США | Франция | Англия |
| Население | США | Россия | Франция | Англия |
| Плотность населения | Англия | Франция | США | Россия |
Рис. 3. Три способа упорядочения
На рисунке 4 приведены ориентированные графы, представляющие отношения "делится" и "меньше" на множестве M = {1, 2, 3, 4} натуральных чисел.
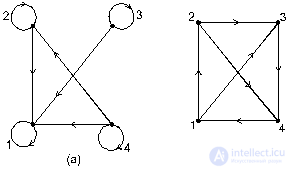
Рис. 4. Графы отношений "делится" (а) и "меньше" (б) на множестве {1,2,3,4}
Пример. М={0;2;5;7}. М2={<0;0>;<0;2>;<0;5>;<0;7>;<2;0>;<2;2>;<2;5>;<2;7>;<5;0>;<5;2>;<5;5>;
<5;7>;<7;0>;<7;2>;<7;5>;<7;7>}.
Из множества М2 выделим подмножество R тех пар <а;b>, в которых a>b. R={<2;0>;<5;0>;<5;2>;<7;0>;<7;2>;<7;5>;}. Множество R определяет отношение «больше» для элементов множества М. Граф, соответствующий данному отношению, изображен на рис. 5. Каждая стрелка направлена от большего числа к меньшему.
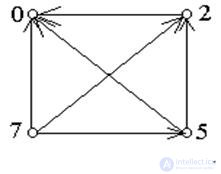

Определение 2.1. Отношение порядка a называется отношением нестрогого порядка на множестве X, если a рефлексивно:
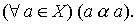
Отношение нестрогого порядка обычно обозначается символом 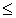 . Если
. Если 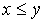 , то говорят, что "элемент x предшествует элементу y" или "y следует за x".
, то говорят, что "элемент x предшествует элементу y" или "y следует за x".
Пример 2.1. Отношение 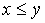 на множестве действительных чисел является отношением нестрогого порядка.
на множестве действительных чисел является отношением нестрогого порядка.
Пример 2.2. На совокупности подмножеств некоторого универсального множества U отношение 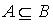 является отношением нестрогого порядка.
является отношением нестрогого порядка.
Пример 2.3. Отношение подчиненности в учреждении является нестрогим порядком на множестве сотрудников учреждения.
Пример 2.4. Отношение 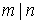 (m делит n) на произвольном подмножестве натуральных чисел является нестрогим порядком. На рисунке 5 приведен граф, соответствующий упорядоченному множеству
(m делит n) на произвольном подмножестве натуральных чисел является нестрогим порядком. На рисунке 5 приведен граф, соответствующий упорядоченному множеству 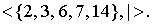
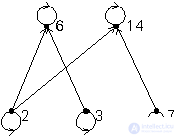
Рис. 5. Граф нестрого упорядоченного множества
Пример 2.5. Тождественное отношение является как отношением эквивалентности, так и отношением нестрогого порядка.
Определение 2.2. Два элемента 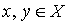 называются сравнимыми элементами упорядоченного множества X, если либо
называются сравнимыми элементами упорядоченного множества X, если либо  , либо
, либо 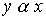 .
.
Несравнимыми элементами в упорядоченном множестве из примера 4 являются, например, элементы 7 и 2, 2 и 3, 3 и 7.
Определение 2.3. Отношение порядка a называется отношением строгого порядка на множестве X, если a антирефлексивно:
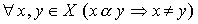 .
.
Отношение строгого порядка обозначается символом <.
Пример 2.6. Пусть f и g - функции с одинаковыми областями определения. Определим отношение > следующим образом: f > g, если для любого x из области определения функции f(x) > g(x). Очевидно, что данное отношение является отношением строгого порядка.
Для функций f и g, изображенных на рисунке 6, имеет место соотношение f > g. Пары функций f и h, а также g и h несравнимы.

Рис. 6. Три функции
Пример 2.7. Алфавитный порядок является отношением строгого порядка на множестве букв.
Пример 2.8. Пусть на множестве X задано отношение строго порядка 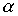 . Как можно задать отношение строгого порядка на множестве
. Как можно задать отношение строгого порядка на множестве 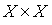 , то есть, как сравнивать пары элементов из множества X? Один из возможных вариантов состоит в следующем. На множестве X определим отношение
, то есть, как сравнивать пары элементов из множества X? Один из возможных вариантов состоит в следующем. На множестве X определим отношение  условием:
условием:

Отношение 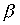 является строгим порядком.
является строгим порядком.
Пример 2.9. Другой способ задания строгого порядка на множестве 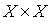 состоит в следующем. Будем считать, что выполнено соотношение (a, b)
состоит в следующем. Будем считать, что выполнено соотношение (a, b) 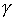 (c, d), если
(c, d), если

Это отношение порядка называется лексикографическим. В общем случае оно определяется следующим образом. Для слов v и w одинаковой длины полагается v < w, если существует такой номер k, что 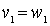 ,
, 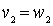 , ...,
, ..., 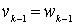 ,
,  , где
, где 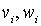 - i-ые буквы слов v и w соответственно. Об этом говорит сайт https://intellect.icu . Для слов
- i-ые буквы слов v и w соответственно. Об этом говорит сайт https://intellect.icu . Для слов 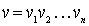 и
и 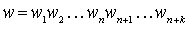 (k > 0) разной длины считается v < w, если
(k > 0) разной длины считается v < w, если 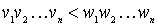 или
или 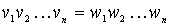 , и w < v, если
, и w < v, если  . Такой способ упорядочения используется в словарях. В этом порядке, например:
. Такой способ упорядочения используется в словарях. В этом порядке, например:
детство < отрочество < юность,
институт < школа < ясли,
12 < 123 < 4.
Как уже отмечалось, упорядоченные множества удобно изображать в виде графов. При этом если 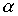 - отношение строго порядка, то граф отношения a не содержит циклов. Верно и обратное: для любого графа G без циклов существует отношение a строгого порядка такое, что граф, ассоциированный с данным отношением, совпадает с транзитивным замыканием графа G. (Транзитивным замыканием графа G называется граф, полученный из графа G добавлением дуг, связывающих каждую вершину a с вершинами, достижимыми из a.) Действительно, пусть G - граф без контуров. Определим на множестве M вершин этого графа отношение
- отношение строго порядка, то граф отношения a не содержит циклов. Верно и обратное: для любого графа G без циклов существует отношение a строгого порядка такое, что граф, ассоциированный с данным отношением, совпадает с транзитивным замыканием графа G. (Транзитивным замыканием графа G называется граф, полученный из графа G добавлением дуг, связывающих каждую вершину a с вершинами, достижимыми из a.) Действительно, пусть G - граф без контуров. Определим на множестве M вершин этого графа отношение 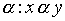 , если существует путь по направлению дуг, ведущий из x в y. Легко видеть, что ввиду отсутствия циклов отношение
, если существует путь по направлению дуг, ведущий из x в y. Легко видеть, что ввиду отсутствия циклов отношение 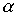 является строгим порядком.
является строгим порядком.
Определение 2.4. Множество X с бинарным отношением  называется связным, если для любых двух различных элементов x и y из X либо
называется связным, если для любых двух различных элементов x и y из X либо  , либо
, либо  .
.
Определение 2.5. Связное отношение порядка на множестве X называется отношением линейного порядка.
Пример 2.10. Лексикографический порядок слов в словаре является линейным порядком.
Пример 2.11. Отношение включения на множестве фигур линейным порядком не является (рис. 7).
Рис. 7. Две несравнимые фигуры
Пример 2.12. Отношение "старше" на множестве людей является линейным порядком.
Пример 2.13. Рассмотрим множество людей. Их можно упорядочить различным образом, например, по росту (рис. 8).

Рис. 8. Шеренга
Упорядочение элементов множества X с помощью отображения его элементов на какое-нибудь упорядоченное множество Y - довольно типичный пример определения порядка.
Соответствующий общий прием упорядочения некоторого множества состоит в следующем. Пусть на множестве X определена инъективная функция
f: X ® R,
принимающая вещественные числовые значения. Зададим отношение < на X условием: x < y, если f(x) < f(y). Так определенное отношение < антирефлексивно, так как не может быть f(x) < f(x). Транзитивность и антисимметричность отношения < столь же очевидна. Наконец, для любой пары различных элементов x, y из X верно либо f(x) < f(y), либо f(y) < f(x), так как f - инъекция. Значит порядок < является линейным. Функция f взаимно однозначно отображает наше множество X на некоторое подмножество множества R вещественных чисел, так что соотношение x < yдля любых элементов множества X равносильно неравенству f(x) < f(y).
Определение 2.6. Пусть на множестве X задано отношение строгого порядка <. Элемент x О X такой, что для всякого y из X, не совпадающего с x, выполнено соотношение x < y (x > y) называется наименьшим (наибольшим).
Определение 2.7. Пусть на множестве X задано отношение строго порядка <. Тогда элемент 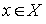 называется минимальным (максимальным) в упорядоченном множестве <X, < >, если не существует никакого элемента y, для которого y < x (соответственно y > x).
называется минимальным (максимальным) в упорядоченном множестве <X, < >, если не существует никакого элемента y, для которого y < x (соответственно y > x).
Если, как обычно, в случае x < y проводить стрелку от x к y, то в графе отношения минимальный элемент - это тот, в который не входят стрелки, а максимальный - из которого не выходят стрелки.
В случае линейного строго порядка минимальный элемент x обладает тем дополнительным свойством, что для всякого 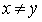 выполнено x < y. Тем самым для случая линейных порядков понятие минимального элемента совпадает с понятием наименьшего элемента. В общем случае может оказаться так, что элемент x минимален, но не находится в соотношении x < y с какими-то иными элементами. Например, на рисунке 5 элемент 2 является минимальным, но не сравним с элементами 3 и 7.
выполнено x < y. Тем самым для случая линейных порядков понятие минимального элемента совпадает с понятием наименьшего элемента. В общем случае может оказаться так, что элемент x минимален, но не находится в соотношении x < y с какими-то иными элементами. Например, на рисунке 5 элемент 2 является минимальным, но не сравним с элементами 3 и 7.
Чтобы понять различие между минимальным и наименьшим элементами, рассмотрим пример.
Пример 2.14. На рисунке 9 изображена диаграмма упорядоченного множества, в котором нет ни наименьшего, ни наибольшего элементов, но в то же время есть ровно 1 минимальный и ровно 1 максимальный элемент.
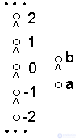
Рис.9. Упорядоченное множество
Рассмотрим подробнее конечные строго упорядоченные множества.
Лемма 2.1. Если на конечном (непустом) множестве X задан линейный строгий порядок, то существует наименьший элемент, и он единственен.
Доказательство. Возьмем произвольный элемент 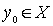 . Если
. Если 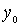 - наименьший элемент, то существование искомого элемента доказано. Если нет, то поскольку < - линейный строгий порядок, существует такой элемент
- наименьший элемент, то существование искомого элемента доказано. Если нет, то поскольку < - линейный строгий порядок, существует такой элемент 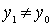 , что
, что 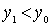 . Опять же либо
. Опять же либо 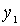 - наименьший, либо существует
- наименьший, либо существует 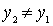 , такой, что
, такой, что  . Будем продолжать это процесс. Предположим, что уже выбрано n + 1 элементов, для которых
. Будем продолжать это процесс. Предположим, что уже выбрано n + 1 элементов, для которых
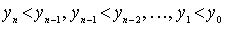 .
.
В силу транзитивности ясно, что 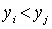 при i > j. Значит, в силу антирефлексивности, все выбранные элементы попарно не равны. Стало быть, ввиду конечности множества X процесс выбора должен прерваться за конечное число шагов. Элемент
при i > j. Значит, в силу антирефлексивности, все выбранные элементы попарно не равны. Стало быть, ввиду конечности множества X процесс выбора должен прерваться за конечное число шагов. Элемент 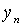 , выбранный на последнем шаге, будет, очевидно, искомым. Итак, для любого
, выбранный на последнем шаге, будет, очевидно, искомым. Итак, для любого 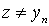 выполнено
выполнено  . Покажем, что этот элемент единственен. В самом деле, пусть существует другой элемент
. Покажем, что этот элемент единственен. В самом деле, пусть существует другой элемент 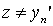 такой, что, для всякого
такой, что, для всякого  . Тогда одновременно выполняется
. Тогда одновременно выполняется 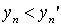 и
и 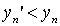 , что невозможно в силу антисимметричности. Лемма доказана.
, что невозможно в силу антисимметричности. Лемма доказана.
Теорема 2.1. Пусть дано отношение линейного строгого порядка < на конечном множестве X. Тогда на X можно выбрать такую нумерацию 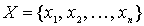 , что соотношение
, что соотношение 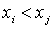 будет выполняться в том и только в том случае, когда i < j.
будет выполняться в том и только в том случае, когда i < j.
Доказательство. Пусть 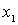 - наименьший элемент во множестве X, выбранный согласно лемме 1. Обозначим через
- наименьший элемент во множестве X, выбранный согласно лемме 1. Обозначим через 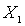 множество
множество 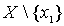 . Обозначим через
. Обозначим через  наименьший элемент множества
наименьший элемент множества 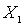 . Ясно, что
. Ясно, что  . Удалим из
. Удалим из 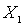 элемент
элемент 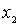 и оставшееся множество обозначим через
и оставшееся множество обозначим через 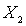 . Его наименьший элемент
. Его наименьший элемент  удовлетворяет условию:
удовлетворяет условию:  . Процедура нумерации уже ясна: перебирая по указанному методу последовательно все элементы из X, мы их выстроим в цепочку:
. Процедура нумерации уже ясна: перебирая по указанному методу последовательно все элементы из X, мы их выстроим в цепочку:
 ,
,
где p - количество элементов в X. В силу транзитивности и антисимметричности ясно, что 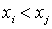 в том и только в том случае, когда i < j. Теорема доказана.
в том и только в том случае, когда i < j. Теорема доказана.
Эта теорема в сущности означает, что любой линейный строгий порядок на конечном множестве X равносилен обычному порядку на некотором отрезке натурального ряда.
С отношением порядка непосредственно связано отношение доминирования.
Определение 2.8. Пусть 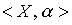 - упорядоченное множество, x и y - его элементы. Будем говорить, что x доминирует над y, если
- упорядоченное множество, x и y - его элементы. Будем говорить, что x доминирует над y, если 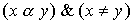 , но не существует такого элемента z О X, что
, но не существует такого элемента z О X, что  .
.
С помощью отношения доминирования можно ввести другой наглядный способ изображения упорядоченных множеств - диаграммы Хассе. На диаграммах каждый элемент изображается точкой на плоскости, и если y доминирует над x, то точки x и y соединяют отрезком, причем точку, соответствующую x, располагают ниже y.
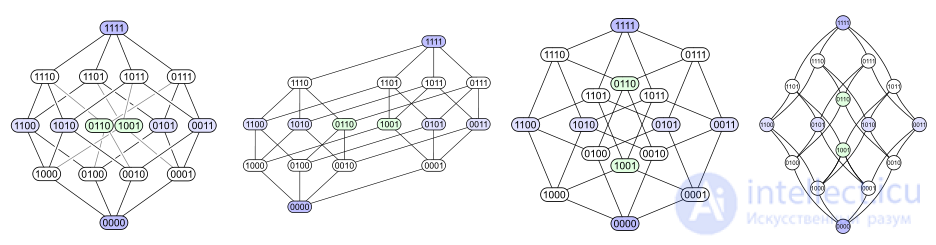
Первая диаграмма демонстрирует структуру уровней. Вторая диаграмма имеет ту же структуру уровней, но на ней некоторые ребра удлинены, чтобы подчеркнуть, что четырехмерный куб является объединением двух трехмерных. Третья диаграмма показывает некоторую внутреннюю симметрию. В четвертой диаграмме вершины упорядочены подобно матрице 4×4.
Рассмотрим три отношения частичного порядка и построим для них диаграммы Хассе.
Пример 2.15. Пусть A = {1, 2, 3}. На множестве всех подмножеств множества A рассмотрим отношение "быть подмножеством". Диаграмма этого упорядоченного множества приведена на рисунке 10(а).
Пример 2.16. Пусть X = {1, 2, 3, 5, 6, 10, 15, 30}. Введем на этом множестве отношение "делится". Диаграмма этого упорядоченного множества приведена на рисунке 10(б).
Пример 2.17. На множестве X = {1, 2, 3, 4, 5, 6, 7, 8} рассмотрим отношение линейного порядка <. Его диаграмма изображена на рисунке 10(в).

Рис. 10. Диаграммы Хассе
Заметим, что диаграммы Хассе первых двух отношений совпадают. Это означает, что эти частично упорядоченные множества имеют одинаковую структуру, причем отличную от структуры третьего упорядоченного множества, хотя оно тоже содержит восемь элементов. Более точно такая общность структуры определяется понятием изоморфизма.
Определение 2.9. Два упорядоченных множества 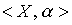 и
и 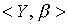 называются изоморфными, если существует биекция
называются изоморфными, если существует биекция 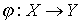 , сохраняющая отношение порядка. Иными словами,
, сохраняющая отношение порядка. Иными словами, 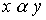 тогда и только тогда, когда
тогда и только тогда, когда 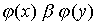 , где
, где 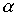 и
и 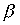 - отношения порядка, заданные на множествах X и Y соответственно.
- отношения порядка, заданные на множествах X и Y соответственно.
Упорядоченные множества, рассмотренные в примерах 1 и 2 изоморфны.
Теорема 2.2. Всякое нестрого упорядоченное множество 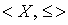 изоморфно некоторой системе подмножеств множества X, нестрого упорядоченной отношением включения.
изоморфно некоторой системе подмножеств множества X, нестрого упорядоченной отношением включения.
Доказательство. Для каждого элемента 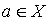 рассмотрим множество
рассмотрим множество 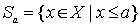 . Тогда
. Тогда 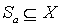 и
и 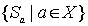 - совокупность всех таких подмножеств. Докажем, что эта система подмножеств, нестрого упорядоченная отношением включения, изоморфна
- совокупность всех таких подмножеств. Докажем, что эта система подмножеств, нестрого упорядоченная отношением включения, изоморфна  . Рассмотрим отображение
. Рассмотрим отображение  такое, что
такое, что 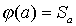 . Тогда
. Тогда  - биекция. Действительно, если
- биекция. Действительно, если 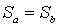 , то, поскольку
, то, поскольку 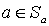 , в силу рефлексивности
, в силу рефлексивности 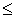 , имеем
, имеем  и
и 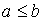 . Аналогично получаем
. Аналогично получаем 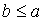 и в силу антисимметричности
и в силу антисимметричности 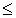 имеем a = b, т. е. отображение
имеем a = b, т. е. отображение 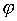 инъективно. Кроме того,
инъективно. Кроме того, 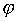 сюръективно, так как у любого подмножества
сюръективно, так как у любого подмножества 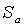 есть прообраз a. Докажем теперь, что отображение сохраняет отношение частичного порядка. Пусть
есть прообраз a. Докажем теперь, что отображение сохраняет отношение частичного порядка. Пусть . Тогда для любого
. Тогда для любого 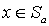 из
из 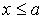 в силу транзитивности отношения
в силу транзитивности отношения 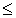 следует
следует 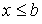 , а значит, и
, а значит, и 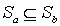 . Если
. Если 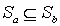 , то, поскольку
, то, поскольку 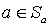 , имеем
, имеем 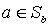 , поетому
, поетому 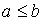 .
.
Перейдем теперь к обсуждению вопросов, связанных с упорядочением по разным критериям. Пусть у нас имеется несколько отношений порядка. Как по ним построить новое отношение порядка?
Исходя из операций над множествами, мы можем определить ряд операций над отношениями. Далее будем полагать, что все отношения заданы на одном и том же множестве X.
Возьмем два отношения 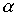 и
и  . Каждому из них соответствует некоторое множество пар (подмножества
. Каждому из них соответствует некоторое множество пар (подмножества  и
и 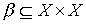 ).
).
Определение 3.1. Пересечением отношений 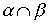 называется отношение, определяемое пересечением соответствующих подмножеств. Ясно, что
называется отношение, определяемое пересечением соответствующих подмножеств. Ясно, что 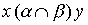 выполнено тогда и только тогда, когда одновременно выполнены соотношения
выполнено тогда и только тогда, когда одновременно выполнены соотношения 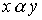 и.
и.
Пример 3.1. Пусть X - множество вещественных чисел, a - отношение "быть не меньше", b - отношение "быть строго больше". Тогда  есть отношение "быть строго больше".
есть отношение "быть строго больше".
Определение 3.2. Объединением отношений  называется отношение, определяемое объединением соответствующих множеств. Соотношение
называется отношение, определяемое объединением соответствующих множеств. Соотношение 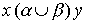 выполнено тогда и только тогда, когда выполнено хотя бы одно их соотношений
выполнено тогда и только тогда, когда выполнено хотя бы одно их соотношений 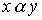 или
или 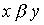 .
.
Пример 3.2. Если 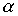 - отношение "больше" на множестве чисел, а
- отношение "больше" на множестве чисел, а 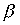 - отношение "равно", то
- отношение "равно", то 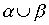 - это отношение
- это отношение 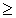 .
.
Можно ввести операции непосредственно не сводящиеся к теоретико-множественным.
Определение 3.3. Обратным отношением называется отношение, определяемое условием: 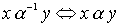 .
.
Пример 3.3. Пусть 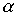 - отношение "делит", тогда
- отношение "делит", тогда  - отношение "делится".
- отношение "делится".
Определение 3.4. Произведением отношений называется отношение, определяемое следующим образом: соотношение 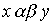 равносильно тому, что существует такой элемент
равносильно тому, что существует такой элемент 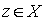 , для которого выполнены соотношения
, для которого выполнены соотношения 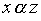 и
и  .
.
Пример 3.4. Пусть 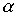 - отношение "быть женой", а
- отношение "быть женой", а 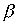 - отношение "быть отцом". Что означает в этом случае соотношение
- отношение "быть отцом". Что означает в этом случае соотношение 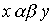 ? По определению существует такой z, что "x - жена z" и "z - отец y". Другими словами, "x есть жена отца y", т.е. "x - мать или мачеха y".
? По определению существует такой z, что "x - жена z" и "z - отец y". Другими словами, "x есть жена отца y", т.е. "x - мать или мачеха y".
Пример 3.5. Пусть 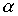 - отношение "быть братом", а
- отношение "быть братом", а 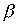 - отношение "быть родителем". Тогда произведение
- отношение "быть родителем". Тогда произведение 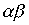 есть отношение "быть братом одного из родителей", т.е. "быть дядей".
есть отношение "быть братом одного из родителей", т.е. "быть дядей".
Прежде чем мы перейдем к теоремам, относящимся к отношению порядка, рассмотрим несколько вспомогательных утверждений (ввиду их простоты мы приводим их без доказательства).
Лемма 3.1. Если отношения 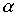 и
и 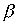 рефлексивны, то рефлексивны и следующие отношения:
рефлексивны, то рефлексивны и следующие отношения:
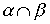 ,
, 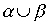 ,
, 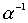 ,
, 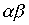 .
.
Лемма 3.2. Если отношения 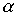 и
и 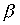 симметричны, то симметричны и следующие отношения:
симметричны, то симметричны и следующие отношения:
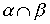 ,
, 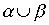 ,
, 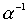 .
.
Лемма 3.3. Чтобы произведение 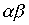 симметричных отношений
симметричных отношений 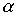 и
и  было симметрично, необходимо и достаточно, чтобы отношения
было симметрично, необходимо и достаточно, чтобы отношения  и
и 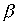 коммутировали.
коммутировали.
Лемма 3.4. Если отношения a и b - антисимметричны, то антисимметричны также и следующие отношения:  ,
, 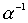 .
.
Антисимметричность может не сохраняться при объединении и произведении.
Лемма 3.4. Если отношения 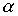 и
и 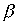 транзитивны, то транзитивны также следующие отношения:
транзитивны, то транзитивны также следующие отношения: 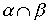 ,
, 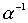 .
.
Из лемм 3.1, 3.2, 3.3, 3.4 вытекают следующие две теоремы.
Теорема 3.1. Если 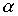 и
и  - строгие порядки (нестрогие порядки), то пересечение
- строгие порядки (нестрогие порядки), то пересечение 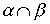 также является строгим порядком (нестрогим порядком).
также является строгим порядком (нестрогим порядком).
Замечание. Пересечение строгого и нестрогого порядка есть строгий порядок.
Свойство "быть линейным порядком" не обязано сохраняться при пересечении. Это проще всего увидеть из следующих соображений. Пусть a - линейный порядок (строгий или нестрогий), тогда 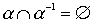 (или = E). Значит,
(или = E). Значит, 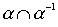 на множестве более чем из одного элемента не является линейным порядком.
на множестве более чем из одного элемента не является линейным порядком.
Теорема 3.2. Если отношение 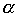 является строгим (нестрогим, линейным) порядком, то и отношение
является строгим (нестрогим, линейным) порядком, то и отношение 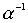 является строгим (нестрогим, линейным) порядком.
является строгим (нестрогим, линейным) порядком.
Объединение порядков в общем случае не является порядком. Это хорошо видно на таком примере. Пусть 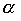 - линейный нестрогий порядок, тогда
- линейный нестрогий порядок, тогда 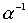 - есть отношение того же типа. Однако, объединение
- есть отношение того же типа. Однако, объединение 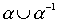 есть полное отношение, и, следовательно, не является порядком. Ниже приведены без доказательства условия, при которых объединение порядков является порядком.
есть полное отношение, и, следовательно, не является порядком. Ниже приведены без доказательства условия, при которых объединение порядков является порядком.
Теорема 3.3. Если 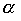 и
и  - строгие порядки, то объединение
- строгие порядки, то объединение 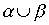 является строгим порядком в том и только том случае, когда
является строгим порядком в том и только том случае, когда
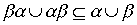 .
.
Теорема 3.4. Для того чтобы объединение  нестрогих порядков
нестрогих порядков 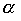 и
и 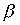 было нестрогим порядком, необходимо и достаточно выполнение условий
было нестрогим порядком, необходимо и достаточно выполнение условий
 ,
,
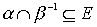 .
.
Произведение порядков 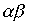 также не обязано быть порядком. Это видно из того хотя бы, что для линейного нестрогого порядка
также не обязано быть порядком. Это видно из того хотя бы, что для линейного нестрогого порядка 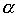 произведение
произведение
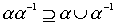
есть полное отношение. Достаточным условием является, например, такое.
Теорема 3.5. Если  и
и 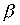 - строгие порядки и выполнены соотношения
- строгие порядки и выполнены соотношения
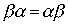 ,
,
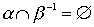 ,
,
то 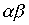 - строгий порядок.
- строгий порядок.
В данной лекции мы рассмотрели определения, разновидности и свойства отношений порядка. Однако, при этом не был затронут достаточно важный вопрос, как на практике строить отношения порядка? Этой проблемой занимаются такие разделы математики как теория выбора и принятия решений, теория голосования в больших и малых группах. Указанный вопрос мы рассмотрим в одной из следующих лекций.
1. Пухначев Ю., Попов Ю. Математика без формул. - М.: АО "Столетие", 1995.
2. Биркгоф Г., Барти Т. Современная прикладная алгебра. - М.: Мир, 1976.
3. Шрейдер Ю. А. Равенство, сходство, порядок. - М.: Наука, 1971.
4. Нефедов В. Н., Осипова В. А. Курс дискретной математики. - М.: Издательство МАИ, 1992.
5. Je. P. Emelchenkov, V. Je. Emelchenkov THE BINARY RELATIONS. RELATIONS OF ORDER Abstract. The relation of order and its characteristics are considered in the article.
Знак равенства
Надеюсь, эта статья про отношение порядка, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое отношение порядка и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.