Лекция
Привет, мой друг, тебе интересно узнать все про ряды, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое ряды, применение рядов, числовые ряды, функциональные ряды, матричные ряды , настоятельно рекомендую прочитать все из категории Ряды.
Ряд, называемый также бесконечная сумма — одно из центральных понятий математического анализа. В простейшем случае ряд записывается как бесконечная сумма чисел :
Краткая запись:
(иногда нумерацию слагаемых начинают не с 1, а с 0)
Здесь — последовательность вещественных или комплексных чисел; эти числа называются членами ряда.
Чтобы присвоить числовому ряду значение суммы, рассмотрим последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:
Если последовательность частичных сумм имеет предел (конечный или бесконечный), то говорят, что сумма ряда равна
При этом, если предел конечен, то говорят, что ряд сходится. Если предел не существует или бесконечен, то говорят, что ряд расходится .
Для выяснения ключевого в анализе вопроса, сходится или нет заданный ряд, предложены многочисленные признаки сходимости.
Числовые ряды и их обобщения (см. ниже о нечисловых рядах) используются повсеместно в математическом анализе для вычислений, для анализа поведения разнообразных функций, при решении алгебраических или дифференциальных уравнений. Разложение функции в ряд можно рассматривать как обобщение задания вектора координатами, эта операция позволяет свести исследование сложной функции к анализу элементарных функций и облегчает численные расчеты . Ряды — незаменимый инструмент исследования не только в математике, но и в физике, астрономии, информатике, статистике, экономике и других науках.
Ряды являются одним из важнейших инструментов математического анализа, так как представляются техническим орудием исследования, очень полезным и удобным, но скромным по-своему принципиальному значению. Поэтому теория рядов заслуживает тщательного изучения. И не столько потому, что многочисленными применениями его проникнуто все здание как самого анализа, так и почти всех опирающихся на него прикладных наук, сколько по той причине, что на сравнительно несложном материале, какой представляет нам собою теория рядов, типичные для всего анализа ходы мыслей, цепи представлений и образов и даже целые логические схемы выступают с особой ясностью и рельефностью.
Античные математики, в соответствии с пифагорейской идеологией, отвергали все актуально бесконечные понятия, в том числе и бесконечные ряды. Тем не менее некоторые ограниченные применения понятия ряда имели место. Например, Архимед для вычисления площади сегмента параболы фактически нашел сумму бесконечной геометрической прогрессии :
Ван дер Варден пишет об этом: «Архимед не говорит о сумме бесконечно убывающей геометрической прогрессии, ему еще не известно выражение „сумма бесконечного ряда“, однако он прекрасно владеет сущностью этого понятия». В нескольких решенных Архимедом задачах на вычисление площади или объема он использует, в современной терминологии, верхние и нижние интегральные суммы с неограниченно возрастающим числом членов. Из-за отсутствия понятия предела для обоснования результата использовался громоздкий метод исчерпывания .
Математики Индии, не связанные пифагорейскими ограничениями, существенно продвинули теорию рядов и успешно ее применяли. Наибольшего успеха в XV—XVI веках добилась Керальская школа астрономии и математики (южная Индия). Для астрономических вычислений керальцы смогли впервые в истории найти разложение тригонометрических и иных функций в бесконечные ряды:
Общей теории таких разложения у них, впрочем, не было, для получения этих формул было проведено спрямление дуги окружности[30][31]. В Европе аналогичный ряд для арктангенса впервые опубликовал Джеймс Грегори в 1671 году, а ряды для синуса и косинуса — Исаак Ньютон в 1666 году.
Из ряда для арктангенса керальцы получили хорошее приближение для числа :
В Европе достижения керальской школы долгое время оставались неизвестными и были переоткрыты независимо.
До примерно XVII века бесконечные ряды в трудах европейских математиков появлялись редко. Заслуживает упоминания труд английского математика XIV века Ричарда Суайнсхеда, который просуммировал ряд:
В XVII веке бесконечные ряды уже вызывают общий интерес и начинают использоваться при решении многих практических задач — приближенные вычисления, интерполирование, теория логарифмов и др.
В 1647 году Грегуар де Сен-Венсан обнаружил связь логарифма и площади под гиперболой (см. рисунок). В 1650 году, исходя из геометрических соображений, итальянский математик Пьетро Менголи опубликовал в трактате «Новые арифметические квадратуры» разложение в бесконечный ряд[33]:
Менголи исследовал также другие ряды и доказал, что гармонический ряд расходится; Менголи также показал, что ряд обратных квадратов сходится, хотя не смог найти его сумму[33].
В 1668 году немецкий математик Николас Меркатор (Кауфман), проживавший тогда в Лондоне, в трактате «Logarithmotechnia» впервые рассмотрел разложение в ряд не числа, а функции, тем самым положив начало теории степенных рядов[33]:
Как универсальный инструмент исследования функций и численных расчетов бесконечные ряды использовали Исаак Ньютон и Готфрид Вильгельм Лейбниц, создатели математического анализа. Еще в середине XVII века Ньютон и Грегори открыли биномиальное разложение для любого, не только целого показателя степени (впервые опубликован в «Алгебре» Валлиса, 1685 год):
Ряд сходится при С помощью этой формулы Ньютон сумел впервые выполнить вычисление дуги эллипса в виде ряда (в современной терминологии, он вычислил эллиптический интеграл)[34]. Ньютон также показал, как с помощью рядов решать уравнения, включая дифференциальные уравнения первого порядка, и исследовать интегралы, не выражающиеся через элементарные функции .
К концу XVII века стали известны разложения в ряды всех элементарных функций. Лейбниц и Грегори открыли (1674) первое в Европе разложение числа (ряд Лейбница):
На рубеже веков (1689—1704) ученик Лейбница Якоб Бернулли опубликовал первую монографию в пяти томах под заголовком «Арифметические предложения о бесконечных рядах и их конечных суммах» (Propositiones arithmeticae de seriebus infinitis carumque summa finita). Он показал применение рядов для решения самых разнообразных задач.
В 1715 году Брук Тейлор опубликовал фундаментальный ряд Тейлора (давно известный, впрочем, Грегори и Ньютону).
Огромный вклад в теорию рядов внес Леонард Эйлер. Он первым сумел найти сумму ряда обратных квадратов, разработал методы улучшения сходимости рядов, начал исследование тригонометрических рядов, предложил понятие обобщенной суммы ряда, пригодное для расходящихся рядов. Само понятие «аналитической функции» было связано с возможностью ее представления в виде степенного ряда.
В XIX веке Коши и Вейерштрасс построили строгие основания анализа и, в частности, строгую теорию рядов. Было введено важное понятие равномерной сходимости, сформулированы разнообразные признаки сходимости.
Бурное развитие получили теория тригонометрических рядов. Еще Даниил Бернулли высказал убеждение, что любую (непрерывную) функцию на заданном промежутке можно представить тригонометрическим рядом[36]. Дискуссии на эту тему продолжались до 1807 года, когда Фурье опубликовал теорию представления произвольных кусочно-аналитических функций тригонометрическими рядами (окончательный вариант содержится в его «Аналитической теории тепла», 1822)[37]. Для разложения функции в ряд
Фурье привел интегральные формулы расчета коэффициентов. Изложение Фурье не было строгим в современном понимании, но уже содержало исследование сходимости большинства полученных им рядов.
Одновременно широкое развитие и применение в XIX веке получили ряды в комплексном анализе, в том числе ряды Лорана. Началось применение рядов в естественных науках — в небесной механике (для решения задачи трех тел), в оптике, теории теплопроводности, ближе к концу века — в теории электромагнетизма.
В XX веке понятие ряда было распространено на широкий класс математических объектов, не обязательно числовых.
Пусть дана бесконечная последовательность чисел: 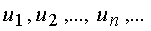 Выражение
Выражение 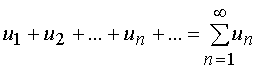 называется числовым рядом.
называется числовым рядом.

Простейшим примером сходящегося ряда является сумма членов бесконечной геометрической прогрессии со знаменателем :
Частичная сумма Предел этого выражения
это и есть сумма бесконечной геометрической прогрессии. Об этом говорит сайт https://intellect.icu . Например, при
получается ряд, сумма которого равна 2:
Десятичную дробь с бесконечной дробной частью можно рассматривать как сумму ряда ; например, число есть сумма следующего ряда:
Более сложным примером является ряд обратных квадратов, сумму которого лучшие математики Европы не могли найти более 100 лет:
Ряд расходится, сумма его бесконечна. Расходится и гармонический ряд:
«Ряд Гранди»
расходится, его частичные суммы колеблются от 1 до 0, поэтому предела частичных сумм не существует, суммы у этого ряда нет.
Положительный ряд — вещественный ряд, все члены которого неотрицательны. У положительных рядов сумма всегда существует, но может быть бесконечна .
Знакочередующийся ряд — вещественный ряд, в котором знаки членов чередуются: плюс, минус, плюс, минус и т. д. Для таких рядов существует простой признак сходимости Лейбница. Знакочередующийся вариант приведенного выше гармонического ряда, в отличие от последнего, сходится :
Говорят, что вещественный или комплексный ряд сходится абсолютно, если сходится ряд из модулей (абсолютных величин) его членов:
Абсолютно сходящийся ряд сходится и в обычном смысле этого понятия. При этом всякий такой ряд обладает важным свойством переместительности: при любой перестановке членов абсолютно сходящегося ряда получается сходящийся ряд с той же суммой. В частности, у положительных сходящихся рядов можно как угодно переставлять члены ряда, на сходимость и на сумму это не влияет.
Если числовой ряд сходится, но не абсолютно, он называется условно сходящимся. Пример:
Сам ряд сходится, но ряд его абсолютных величин (гармонический ряд) расходится.
Свойства условно сходящихся рядов.
Пусть заданы сходящиеся ряды и
. Тогда:
Если оба ряда сходятся к и
соответственно, то их сумма и разность также сходятся. Сумма сходящегося и расходящегося рядов всегда расходится[11]:
,
Если оба ряда сходятся абсолютно, то сумма и разность этих рядов также сходятся абсолютно.
Если хотя бы один из исходных рядов сходится абсолютно, то произведение рядов сходится.
Ряд может сходиться лишь в том случае, когда член
(общий член ряда) с возрастанием его номера стремится к нулю:
Это необходимый признак сходимости ряда, но он не является достаточным — у гармонического ряда, например, общий член с ростом номера неограниченно уменьшается, тем не менее ряд расходится. Если же общий член ряда не стремится к нулю, то ряд заведомо расходится.
Свойство 1. Если ряд
(1.1)
сходится и его сумма равна S, то ряд
(1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд (1.2) расходится.
Свойство 2 (ассоциативный закон). В сходящемся ряде можно произвольно объединять соседние члены в группы без нарушения их порядка.
Этим свойством можно воспользоваться для доказательства расходимости ряда: если после указанной группировки получается расходящийся ряд, то и исходный ряд также расходится.
До сих пор неизвестно, сходится ли «ряд Флинт Хиллз» (Flint Hills Series)[16]:
Если удастся доказать, что этот ряд сходится, то как следствие получится важный факт: мера иррациональности числа меньше, чем 2,5.
Известно, что сумма ряда обратных квадратов и суммы других рядов с обратными четными степенями выражаются через степени числа но мало что известно про сумму обратных кубов («константу Апери»):
.
Никто пока не сумел связать это значение с классическими константами или элементарными функциями.
Понятие бесконечного ряда и его суммы можно ввести не только для чисел, но и для других математических объектов, для которых определены сложение и понятие близости, позволяющее определить предел. Например, в анализе широко используются ряды из функций: степенные ряды, ряды Фурье, ряды Лорана. Членами ряда могут быть также векторы, матрицы и др.
Ряд (или бесконечная сумма) в математике — последовательность элементов (членов данного ряда) некоторого топологического векторного пространства, рассматриваемая вместе с множеством частичных сумм членов ряда (частичные суммы определяются так же, как и в числовых рядах). Если для последовательности частичных сумм определен предел:
то значение
называется суммой данного ряда, а сам ряд называется сходящимся (в противном случае — расходящимся).
Ряды всегда можно почленно складывать или вычитать, причем сумма и разность сходящихся рядов также сходятся. Если члены рядов берутся из кольца или поля, то ряды сами образуют кольцо относительно сложения и произведения Коши.
Ряд называется функциональным, если все его члены — функции, определенные на некотором множестве:
краткая запись:
Частичные суммы в этом случае также являются функциями, заданными на том же множестве. Ряд называется сходящимся на множестве , если при любом фиксированном
сходится числовой ряд :
Множество называется областью сходимости ряда. Сумма ряда, очевидно, также является функцией на
Пример — разложение в ряд рациональной дроби:
Этот ряд сходится в интервале .
Среди основных типов функциональных рядов:
Кроме определенной выше «поточечной» сходимости, в разных пространствах могут быть использованы и другие нормы близости, от которых зависит существование предела частичных сумм. Например, можно определить «чебышевскую норму»[19].
Вообще говоря, свойства суммы могут отличаться от свойств членов ряда — например, сумма ряда непрерывных функций может не быть непрерывной[20].
Говорят, что сходящийся на множестве функциональный ряд равномерно сходится (на этом множестве)[21], если последовательность частичных сумм ряда равномерно сходится на
.
Существуют несколько признаков, позволяющих убедиться в равномерной сходимости ряда[21]:
Важность понятия равномерной сходимости ряда показывают следующие теоремы (все функции считаются вещественными).
сходятся на , причем ряд производных сходится равномерно, то сумма ряда имеет производную, и дифференцировать ряд можно почленно[23]:
Условие равномерной сходимости гарантирует, что ряд справа сходится.
Пример неравномерно сходящегося степенного ряда — геометрическая прогрессия В промежутке
она сходится к функции
но не равномерно (о чем свидетельствует бесконечный скачок суммы при приближении к 1).
В кольце числовых квадратных матриц фиксированного порядка назовем
-окрестностью матрицы
множество матриц, все компоненты которых отличаются от соответствующих компонент
меньше, чем на
Опираясь на такую топологию, предел последовательности матриц определяется покомпонентно[26], то есть матрица
является пределом последовательности матриц
, если каждая ее компонента
является пределом соответствующей последовательности
Теперь можно определить по общим правилам ряды из числовых матриц, понятие сходимости ряда (в том числе абсолютной сходимости) и суммы сходящегося ряда. Другими словами, ряд матриц порядка сходится, если сходятся
рядов его компонент, и суммой будет матрица, содержащая соответствующие пределы этих рядов[26].
Степенной ряд для матриц имеет вид[26]:
где — заданные числовые коэффициенты,
— единичная матрица,
— матрица неизвестных. Этот ряд равносилен системе из
числовых рядов. Для оценки его сходимости составим обычный степенной ряд из комплексных чисел:
Пусть радиус сходимости этого ряда равен Тогда верны следующие теоремы[26]:
Пример степенного ряда из матриц см. в статье Экспонента матрицы. С помощью рядов можно определить стандартные функции для квадратных матриц (например, синус).
Важное место в статистике занимает описание изменений показателей во времени или в динамике. Ряд динамики образуется в результате сводки и обработки материалов периодического статистического наблюдения.
Итак, ряд динамики — это числовые значения статистических показателей, изменяющихся во времени и расположенных в хронологической последовательности.
Ряд динамики включает два обязательных элемента:
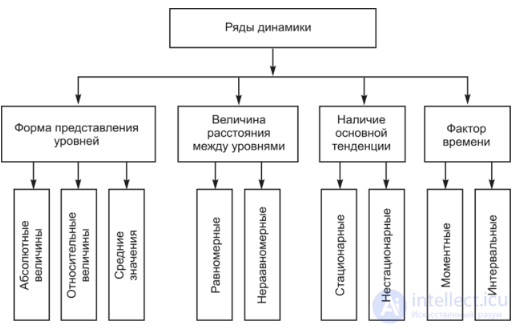
Существуют различные виды рядов динамики. Классификация показана на рис.
Ряд Фурье́ — представление функции с периодом
в виде ряда
Этот ряд может быть также записан в виде
где
— амплитуда
-го гармонического колебания,
— круговая частота гармонического колебания,
— начальная фаза
-го колебания,
—
-я комплексная амплитуда
В более общем виде, рядом Фурье элемента некоторого пространства функций называется разложение этого элемента по полной системе ортонормированных функций или другими словами по базису, состоящему из ортогональных функций. В зависимости от используемого вида интегрирования говорят о рядах Фурье — Римана, Фурье — Лебега и т. п.
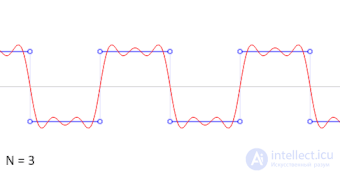
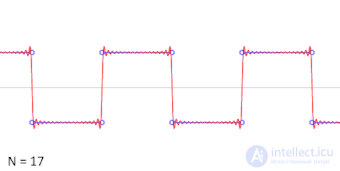
Результаты добавления членов ряда Фурье при аппроксимации разрывной кусочно-постоянной функции. Выбросы на фронтах обусловлены неравномерной сходимостью ряда Фурье в точках разрыва (явление Гиббса
Существует множество систем ортогональных многочленов и других ортогональных функций (например, функции Хаара, Уолша и Котельникова), по которым может быть произведено разложение функции в ряд Фурье.
Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведет себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свертке функций.
Существуют многочисленные обобщения рядов Фурье в различных разделах математики. Например, любую функцию на конечной группе можно разложить в ряд, аналогичный ряду Фурье, по матричным элементам неприводимых представлений этой группы (теорема полноты).
Обобщением понятия ряда является понятие двойного ряда, члены которого нумеруются.не одним, а двумя индексами.
Обобщением понятия суммы ряда является понятие суммирующей функции ряда, выбор которой делает понятие суммы расходящегося (в классическом смысле) ряда приемлемым. Предложено множество вариантов такого обобщения: сходимость по Пуассону — Абелю, Борелю, Чезаро, Эйлеру, Ламберту и другие
ряды имеют самые разнообразные приложения
приближенные вычисления. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «неберущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.
Пример Вычислить приближенно с точностью до 0,0001: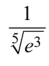
Решение.
Для вычисления 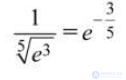 запишем ряд
запишем ряд 
при х = -3/5 , принадлежащем области сходимости  :
:

Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда мы допустим погрешность 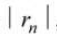 не превышающую первого отброшенного члена (по абсолютной величине), т.е.
не превышающую первого отброшенного члена (по абсолютной величине), т.е.
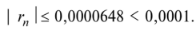
Итак, 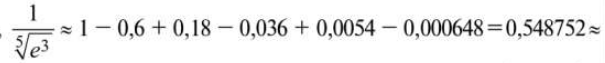
РЯДЫ В РОЛИ АППАРАТА ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ
Среди различных аналитических аппаратов, могущих в этом смысле служить орудиями исследования функций, первое место по своей простоте, гибкости, прозрачности и удобству употребления, без сомнения, занимают функциональные ряды. Идея этого важнейшего аналитического аппарата очень проста: функция, которую мы хотим исследовать, представляется как предел последовательности других, более простых и доступных исследованию функций (частичных сумм изображающего ряда); если такая частичная сумма на всем рассматриваемом участке весьма близка к изучаемой функции, то мы имеем основание рассчитывать из свойств этой приближенной частичной суммы узнать, хотя бы приближенно, некоторые свойства изучаемой функции; в частности, умея приближенно вычислять, при тех или других значениях аргумента, значения этих частичных сумм, мы тем самым имеем метод для приближенного вычисления соответствующих значений изучаемой функции.
Применение рядов к решению дифференциальных уравнений
Пусть требуется проинтегрировать дифференциальное уравнение второго порядка
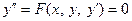 . (1)
. (1)
Если его решение не выражается через элементарные функции в конечном виде или обычные способы решения слишком трудоемки, то в отдельных случаях его решение (частное или общее) удается отыскать в виде некоторого степенного ряда.
ПРИМЕНЕНИЕ РЯДОВ В ПРОГАММИРОВАНИИ
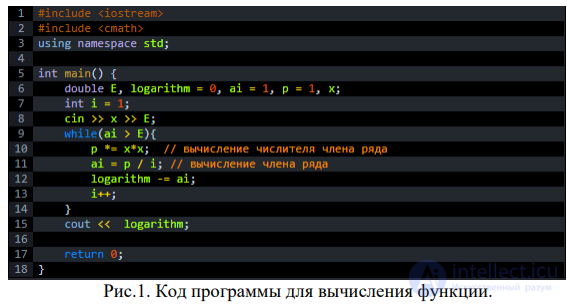
Правило Ти́циуса — Бо́де (известно также как закон Бо́де) представляет собой эмпирическую формулу, приблизительно описывающую расстояния между планетами Солнечной системы и Солнцем (средние радиусы орбит). Правило было предложено Иоганном Тициусом в 1766 году и получило известность благодаря работам Иоганна Боде в 1772 году.
Правило формулируется следующим образом.
|
К каждому элементу последовательности |
Последовательность — геометрическая прогрессия, кроме первого числа. То есть,
.
Эту же формулу можно записать по-другому:
Встречается также другая формулировка:
|
Для любой планеты среднее расстояние от ее орбиты до орбиты самой внутренней планеты (в Солнечной системе — Меркурия) в два раза больше, чем среднее расстояние от орбиты предыдущей планеты до орбиты самой внутренней планеты: |
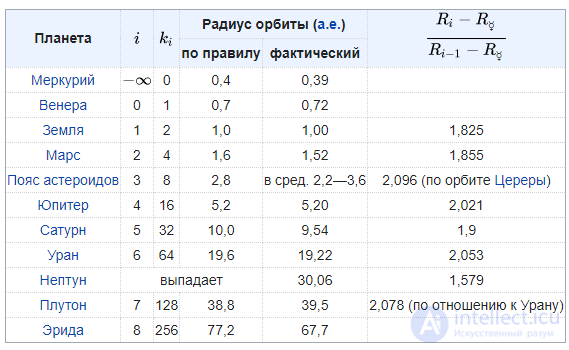
Результаты вычислений приведены в таблице (где ). Видно, что этой закономерности соответствует и пояс астероидов, а Нептун, напротив, из закономерности выпадает, причем его место занимает Плутон, хотя он, согласно решению XXVI Ассамблеи МАС исключен из числа планет.
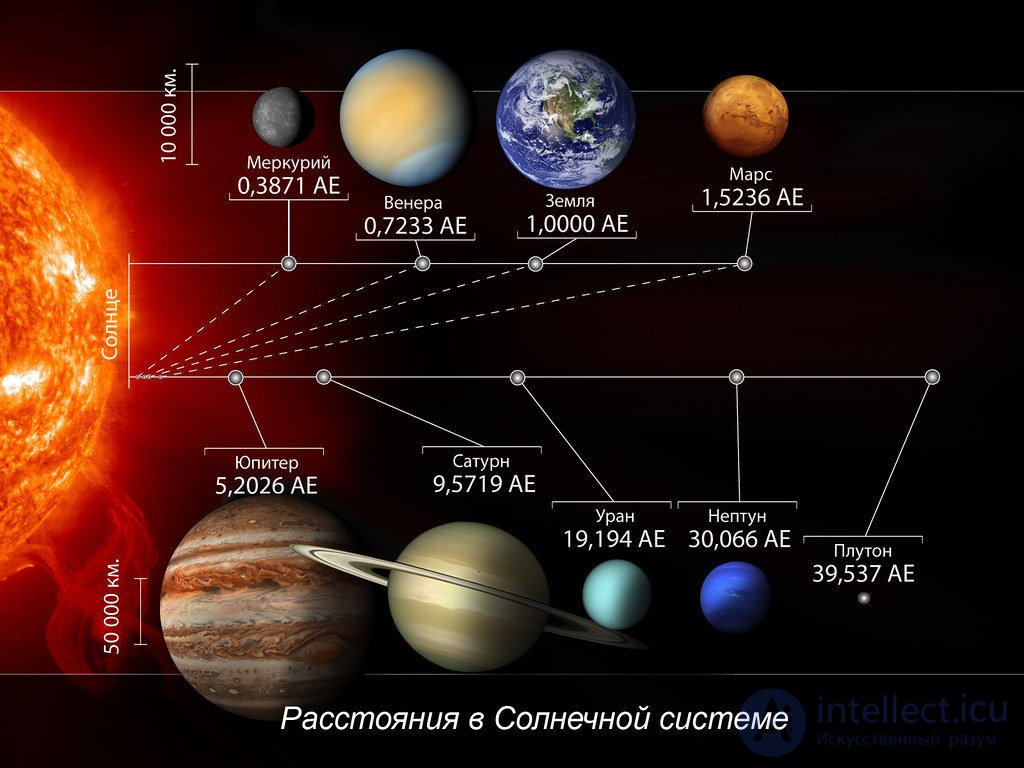
Когда Тициус впервые сформулировал это правило, ему удовлетворяли все известные в то время планеты (от Меркурия до Сатурна), имелся лишь пропуск на месте пятой планеты. Тем не менее, правило не привлекло большого внимания до тех пор, пока в 1781 году не был открыт Уран, который почти точно лег на предсказанную последовательность. После этого Боде призвал начать поиски недостающей планеты между Марсом и Юпитером. Именно в том месте, где должна была располагаться эта планета, была обнаружена Церера. Это вызвало большое доверие к правилу Тициуса — Боде среди астрономов, которое сохранялось до открытия Нептуна. Когда выяснилось, что, кроме Цереры, примерно на том же расстоянии от Солнца находится множество тел, формирующих пояс астероидов, была выдвинута гипотеза, что они образовались в результате разрушения планеты (Фаэтона), которая раньше находилась на этой орбите.
Тебе нравиться ряды? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое ряды, применение рядов, числовые ряды, функциональные ряды, матричные ряды и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Ряды
Комментарии
Оставить комментарий
Ряды
Термины: Ряды