Лекция
Привет, Вы узнаете о том , что такое неинерциальные системы отсчета, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое неинерциальные системы отсчета, силы инерции, сила кориолиса, маятник фуко , настоятельно рекомендую прочитать все из категории Физические основы механики.
Как уже отмечалось, законы Ньютона выполняются только в инерциальных системах отсчета.
Системы отсчета, движущиеся относительно инерциальной системы отсчета с ускорением, называются неинерциальными.
В неинерциальных системах отсчета несправедлив первый закон Ньютона. Каждый знает, что при рывке автобуса с места пассажиров толкает в обратную сторону. Автобус — неинерциальная система, и в ней никаких видимых воздействий на пассажиров со стороны других тел не оказывалось, но они, тем не менее, не сохранили состояние покоя.
В принципе использование неинерциальных систем отсчета ничем не запрещено. Мы сами живем в такой системе — на Земле, вращающейся вокруг собственной оси и движущейся вокруг Солнца. В такой системе отсчета законы динамики выглядят значительно сложнее. В сущности, спор между системами мира по Птолемею и Копернику касался вопроса, какую из систем отсчета использовать: связанную с Землей или с Солнцем. Последняя, как известно, оказалась гораздо удобнее. Система отсчета, связанная с Землей, неинерциальна в гораздо большей степени, в ней движения планет выглядели сложными и запутанными. Но никто не запрещает пользоваться и системой, связанной с Землей. Надо только соответствующим образом подправить законы динамики.
Возьмем уединенное тело, не подверженное воздействию других тел. Если следить за ним из неинерциальной системы отсчета, то, подобно пассажирам автобуса, оно не будет оставаться в покое или двигаться прямолинейно и равномерно. А раз его скорость меняется, то отлично от нуля ускорение тела. Значит, умножив ускорение на массу, мы можем по второму закону Ньютона найти действующую на тело силу. Такого рода силы не совсем обычны в том смысле, что мы не можем указать тела, со стороны которых они действуют. В остальном они ничем не отличаются от прочих сил, с которыми мы уже знакомы.
Силы, действующие на тела в неинерциальных системах отсчета, и не обусловленные взаимодействием этих тел с другими телами, называются силами инерции.
Иногда говорят о фиктивности таких сил, понимая под этим то, что в инерциальной системе отсчета их не было бы. Р. Фейнман в своих «Фейнмановских лекциях по физике» (Москва, «МИР», 1967, страница 225) называет их «псевдосилами».
Этот аргумент может показаться не вполне убедительным. Что за беда, если в одной системе отсчета тело имеет ускорение (на него действует сила), в другой это ускорение равно нулю (нет сил)? При переходе из одной системы отсчета к другой меняется скорость тела, его энергия. После знакомства с СТО мы знаем, что меняются длины и временные интервалы. Поэтому естественно и на силы взглянуть с этой же точки зрения. Итак, силы инерции вполне реальны, их можно измерить, но наблюдаются они только в неинерциальных системах отсчета. Они не являются следствием взаимодействия данного тела с другими телами, они являются следствием неинерциальности системы отсчета. Для одного и того же тела эти силы различны и имеют разные свойства в разных неинерциальных системах отсчета в зависимости от характера движения неинерциальной системы отсчета относительно инерциальной. Однако, как уже было сказано, их проявления вполне реальны и измеримы.
Видео 8.1. «Поступательная» сила инерции: натюрморт с шампанским
Видео 8.2. «Поступательная» сила инерции: опыт с гирей на тележке
Рассмотрим шарик, подвешенный на нити, точка подвеса которого 0' движется с ускорением a относительно некоторой инерциальной системы отсчета К. Нить подвеса отклоняется от вертикали на некоторый угол 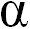 . Угол этот таков, чтобы равнодействующая F силы натяжения нити T и силы тяжести mg привела к движению шарика с ускорением a:
. Угол этот таков, чтобы равнодействующая F силы натяжения нити T и силы тяжести mg привела к движению шарика с ускорением a:
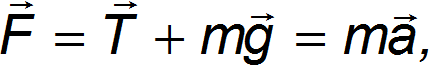
откуда
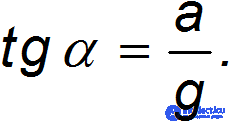
Так выглядит описание явления с точки зрения наблюдателя в инерциальной системе отсчета К (рис. 8.1).
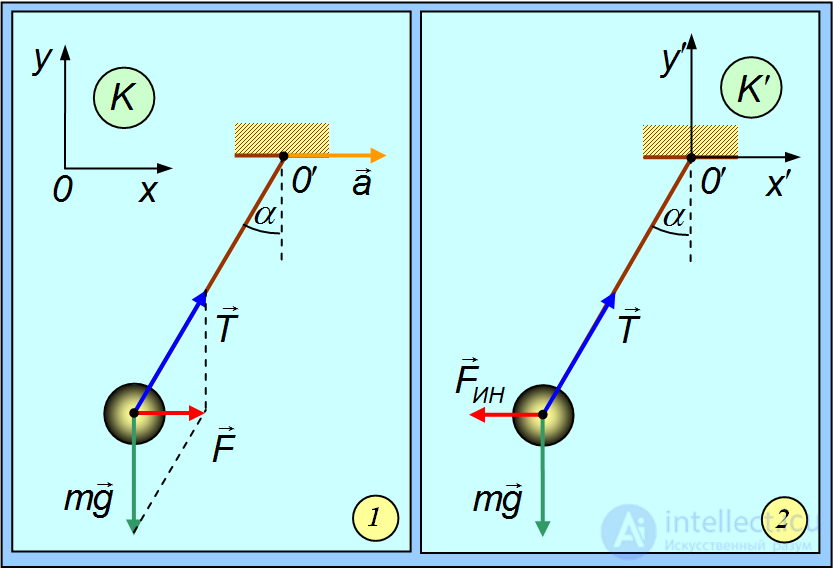
Рис. 8.1. Движение шарика на нити, точка подвеса которого движется с ускорением: 1 — с точки зрения наблюдателя в инерциальной системе отсчета; 2 — с точки зрения наблюдателя в движущейся неинерциальной системе отсчета
Свяжем теперь систему отсчета К' с точкой подвеса 0'. Эта система будет неинерциальной, так как она движется с ускорением a относительно инерциальной системы К. Мы пользуемся нерелятивистской механикой, так что угол отклонения нити, равно как и силы T, mg для обоих наблюдателей одинаковы. Но для наблюдателя К' шарик находится в покое (см. рис. 1–2) С другой стороны, наблюдатель К' видит, что результирующая сил T и mg не равна нулю. Поэтому наблюдатель К' приходит к выводу, что в его системе отсчета действует какая-то сила — сила инерции 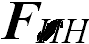 , которой не было в инерциальной системе отсчета К. Выражение для силы инерции получаем из условия равновесия шарика в системе К', то есть из равенства нулю трех сил:
, которой не было в инерциальной системе отсчета К. Выражение для силы инерции получаем из условия равновесия шарика в системе К', то есть из равенства нулю трех сил:
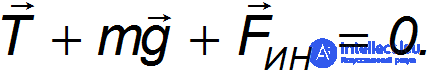
Отсюда
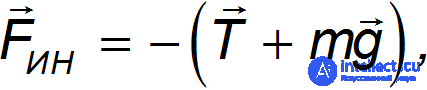
и из уравнения второго закона Ньютона для тела следует выражение для силы инерции при поступательном движении неинерциальной системы отсчета с ускорением a:
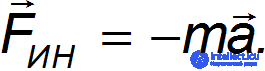
Этот же результат верен в общем случае для произвольного движения материальной точки в движущейся поступательно неинерциальной системе отсчета К'. Пусть скорость ее движения относительно инерциальной системы отсчета К описывается функцией 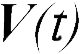 , а оси обеих систем остаются параллельными. Пусть скорость движения материальной точки в системе К меняется по закону
, а оси обеих систем остаются параллельными. Пусть скорость движения материальной точки в системе К меняется по закону 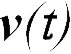 . Значит, в инерциальной системе К согласно второму закону Ньютона на точку действует сила
. Значит, в инерциальной системе К согласно второму закону Ньютона на точку действует сила
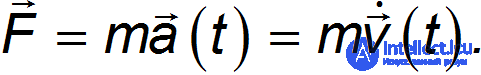
Скорость этой же точки для наблюдателя в системе К' равна
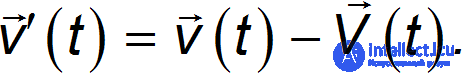
Значит в неинерциальной системе отсчета К' на точку действует сила
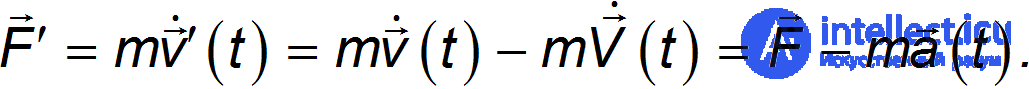
Таким образом, и в этом случае сила инерции определяется формулой
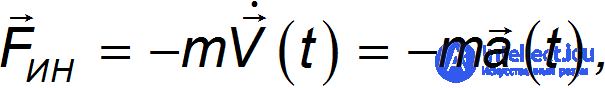
где 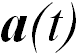 — ускорение поступательного движения неинерциальной системы относительно инерциальной.
— ускорение поступательного движения неинерциальной системы относительно инерциальной.
Видео 8.3. Маятник на тележке ускоренно скатывающейся с наклонной плоскости
Заметим, что благодаря равенству гравитационной и инертной масс, обсуждавшемуся в главе 5.4, наблюдатель в системе К' может утверждать, что в его системе имеется однородное гравитационное поле, заставляющее тела «падать» с ускорением
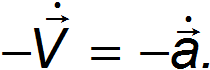
Эйнштейн сформулировал принцип эквивалентности неинерциальных систем и гравитационных полей и построил на этой основе общую теорию относительности (ОТО) или теорию гравитации.
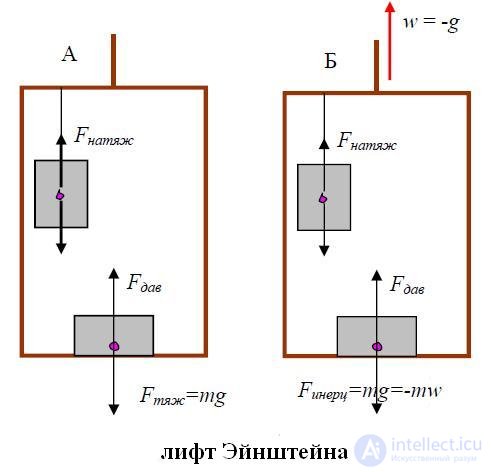
Рис. 8.2. Лифт Эйнштейна
Возникновение силы инерции при поступательном ускоренном движении системы отсчета демонстрируется в опыте, показанном на рис. 8.2.
Представим себе диск, равномерно вращающийся с угловой скоростью  . Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной (рис. 8.3).
. Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной (рис. 8.3).
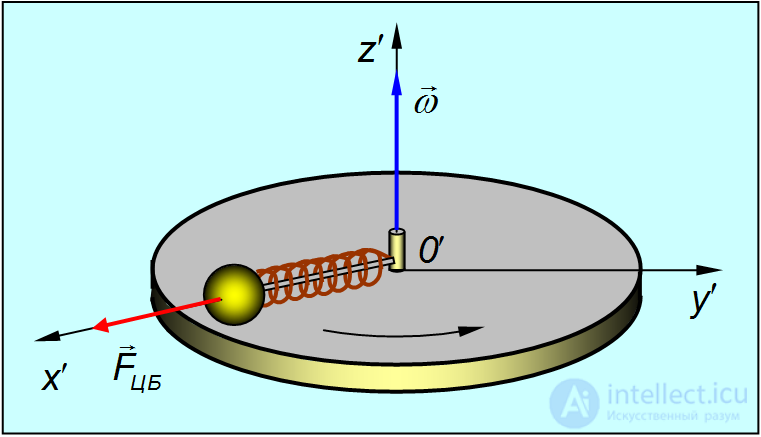
Рис. Об этом говорит сайт https://intellect.icu . 8.3. Центробежная сила инерции в системе отсчета, связанной с вращающимся диском
Шарик покоится относительно диска и занимает на спице такое положение, при котором сила натяжения пружины 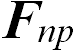 оказывается равной произведению массы шарика
оказывается равной произведению массы шарика 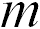 на нормальное (центростремительное) ускорение (при равномерном вращении диска тангенциальное ускорение шарика, очевидным образом, равно нулю)
на нормальное (центростремительное) ускорение (при равномерном вращении диска тангенциальное ускорение шарика, очевидным образом, равно нулю)
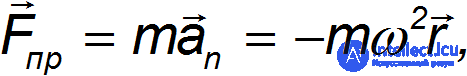
где 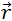 — радиус-вектор, проведенный к шарику из центра диска (см. рис. 8.3). Но так рассуждает наблюдатель, смотрящий на вращение диска из инерциальной системы отсчета. Свяжем с диском вращающуюся неинерциальную систему отсчета К', в которой диск вместе с шариком покоится. Условие равновесия шарика в этой системе имеет вид:
— радиус-вектор, проведенный к шарику из центра диска (см. рис. 8.3). Но так рассуждает наблюдатель, смотрящий на вращение диска из инерциальной системы отсчета. Свяжем с диском вращающуюся неинерциальную систему отсчета К', в которой диск вместе с шариком покоится. Условие равновесия шарика в этой системе имеет вид:
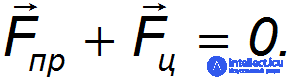
Наблюдатель во вращающейся системе отсчета объясняет равновесие шарика наличием силы инерции
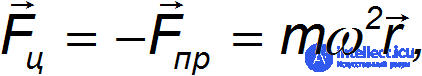
направленной от центра диска 0' по радиус-вектору 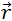 .
.
Сила инерции, действующая на материальную точку в равномерно вращающейся с угловой скоростью ω системе отсчета, называется центробежной силой инерции:
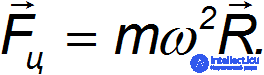
Здесь 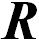 — вектор, проведенный к материальной точке от оси вращения ортогонально последней. Мы ввели его, чтобы отличить от радиус-вектора
— вектор, проведенный к материальной точке от оси вращения ортогонально последней. Мы ввели его, чтобы отличить от радиус-вектора 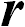 в том случае, когда начало координат лежит на оси вращения, но не в плоскости вращения материальной точки.
в том случае, когда начало координат лежит на оси вращения, но не в плоскости вращения материальной точки.
Видео 8.4. Центробежная сила инерции: подвешенные шарики
При произвольном положении начала отсчета на оси вращения, радиус-вектор некоторой материальной точки всегда можно представить в виде
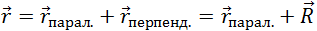
где 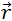 парал.— параллельная оси вращения, более того, лежащая на оси вращения (напомним: начинается вектор
парал.— параллельная оси вращения, более того, лежащая на оси вращения (напомним: начинается вектор 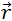 на оси вращения) составляющая радиус вектора
на оси вращения) составляющая радиус вектора 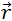 , а
, а 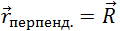 — перпендикулярная к оси вращения его составляющая, начинающаяся на оси вращения, в центре той окружности, по которой движется рассматриваемая точка. С помощью известной формулы
— перпендикулярная к оси вращения его составляющая, начинающаяся на оси вращения, в центре той окружности, по которой движется рассматриваемая точка. С помощью известной формулы
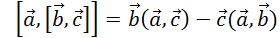
учитывая, что векторное произведение 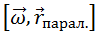 и скалярное произведение
и скалярное произведение 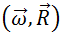 равны нулю всегда, можно показать, что выражение для центробежной силы инерции представляется в виде
равны нулю всегда, можно показать, что выражение для центробежной силы инерции представляется в виде
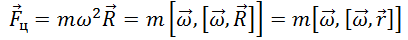
Таким образом, в общем случае, при произвольном выборе начала отсчета на оси вращения, для любого положения материальной точки, действующую на нее центробежную силу инерции, можно записать в виде
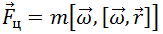
Видео 8.5. «Поразительное» поведение цепи — и здесь не обошлось без центробежной силы инерции. Цепь легкая, почти без трения между звеньями
Видео 8.6. «Поразительное» поведение цепи 2. Цепь тяжелая, с большим трением между звеньями
Пример. Сосуд с жидкостью вращается с угловой скоростью  вокруг вертикальной оси (рис. 8.4). Найдем форму поверхности жидкости.
вокруг вертикальной оси (рис. 8.4). Найдем форму поверхности жидкости.
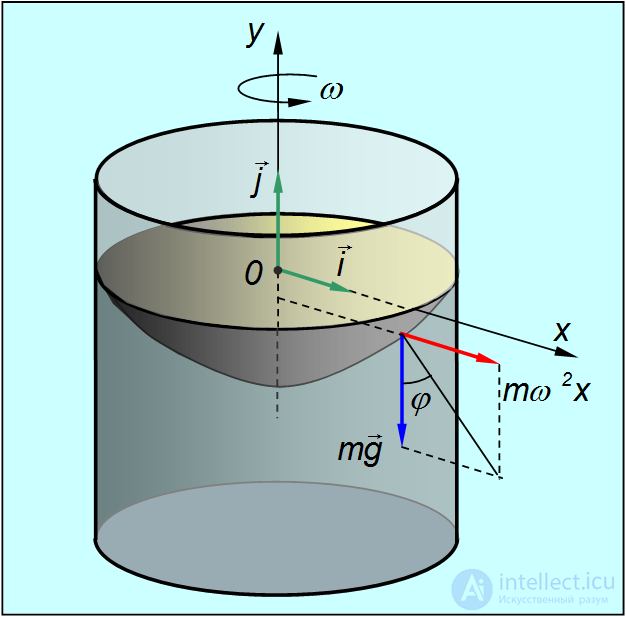
Рис. 8.4. Форма поверхности вращающейся жидкости
Задачу решаем в системе отсчета, вращающейся вместе с жидкостью. В этой системе жидкость неподвижна, но кроме силы тяжести на нее действует центробежная сила инерции. Поверхность жидкости симметрична относительно оси вращения. Рассмотрим сечение этой поверхности какой-нибудь вертикальной плоскостью, содержащей ось вращения, которую мы примем за ось 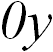 .
.
Возьмем на поверхности элемент жидкости массой 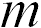 , расположенный в точке с координатой
, расположенный в точке с координатой 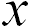 . На него действует сила тяжести
. На него действует сила тяжести 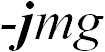 и центробежная сила инерции
и центробежная сила инерции 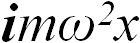 (здесь координата
(здесь координата 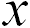 есть расстояние от оси вращения, а
есть расстояние от оси вращения, а 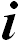 и
и 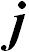 — единичные орты). Результирующая этих сил наклонена к вертикали под углом
— единичные орты). Результирующая этих сил наклонена к вертикали под углом 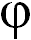 таким, что
таким, что
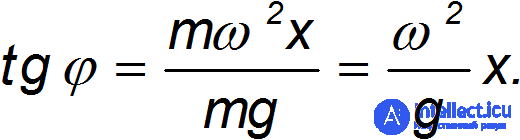
Поверхность жидкости, описываемая функцией 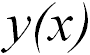 , всегда располагается ортогонально линии действия внешних сил. Как известно, тангенс того же угла можно найти как отношение приращений
, всегда располагается ортогонально линии действия внешних сил. Как известно, тангенс того же угла можно найти как отношение приращений
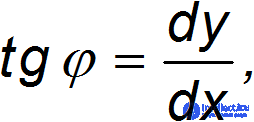
то есть как производную. Получаем уравнение
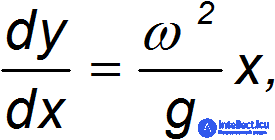
которое легко интегрируется:
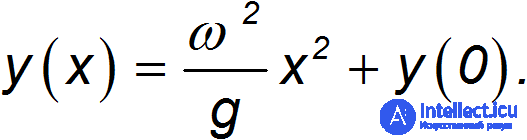
Это уравнение, как известно, описывает параболу. Вращение этой параболы задает параболоид вращения. Таким образом, поверхность вращающейся жидкости принимает форму параболоида вращения. При 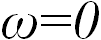 имеем
имеем 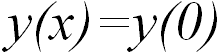 , то есть плоскую горизонтальную поверхность.
, то есть плоскую горизонтальную поверхность.
Видео 8.7. Циркулярная «пила» из бумаги – неожиданное применение центробежной силы инерции
Видео 8.8. сила кориолиса : траектория движения шарика по вращающейся платформе
В предыдущем параграфе было рассмотрено тело, неподвижное во вращающейся системе отсчета. Если во вращающейся системе отсчета тело движется, то, помимо центробежной силы, на него будет действовать еще одна сила инерции, называемая силой Кориолиса или кориолисовой силой инерции.
Пусть шарик массой  движется без трения вдоль радиуса диска (рис. 8.5) с постоянной скоростью
движется без трения вдоль радиуса диска (рис. 8.5) с постоянной скоростью 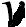 , направленной в некую точку
, направленной в некую точку 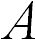 на краю диска.
на краю диска.
Рис. 8.5. Отклонение шарика, движущегося во вращающейся системе отсчета
Если диск не вращается, то шарик движется по радиусу и попадает в точку  . Если же диск привести во вращение с угловой скоростью
. Если же диск привести во вращение с угловой скоростью  , то к моменту достижения шариком края диска на месте точки
, то к моменту достижения шариком края диска на месте точки  окажется другая точка
окажется другая точка 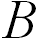 . Если шарик оставляет след, то он прочертит свою траекторию относительно диска — кривую линию
. Если шарик оставляет след, то он прочертит свою траекторию относительно диска — кривую линию 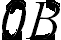 . При этом на шарик не действуют никакие видимые силы, и относительно инерциальной системы он по-прежнему движется с постоянной скоростью
. При этом на шарик не действуют никакие видимые силы, и относительно инерциальной системы он по-прежнему движется с постоянной скоростью 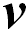 . Скорость же шарика относительно диска
. Скорость же шарика относительно диска 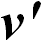 изменяла свое направление. Значит, в системе отсчета, связанной с вращающимся диском, на шарик действовала сила инерции, не параллельная скорости
изменяла свое направление. Значит, в системе отсчета, связанной с вращающимся диском, на шарик действовала сила инерции, не параллельная скорости 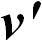 . Стало быть, она не была направлена по радиусу, откуда следует, что эта сила отлична от рассмотренной выше центробежной силы инерции. Ее и называют силой Кориолиса.
. Стало быть, она не была направлена по радиусу, откуда следует, что эта сила отлична от рассмотренной выше центробежной силы инерции. Ее и называют силой Кориолиса.

Рис. 8.6 Движение шарика по гладкой поверхности вращающегося диска. Сверху — с точки зрения внешнего наблюдателя. Снизу — с точки зрения наблюдателя, неподвижного относительно диска
Найдем выражение для силы Кориолиса в частном случае (рис. 8.7), когда частица массой  движется относительно вращающейся системы отсчета К' равномерно по окружности, лежащей в плоскости, перпендикулярной к оси вращения
движется относительно вращающейся системы отсчета К' равномерно по окружности, лежащей в плоскости, перпендикулярной к оси вращения  , с центром на оси вращения.
, с центром на оси вращения.
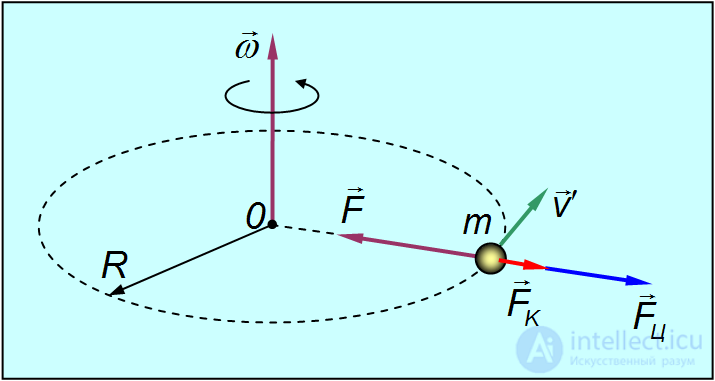
Рис. 8.7. К выводу выражения для силы Кориолиса
Скорость частицы относительно вращающейся системы К' обозначим через 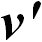 . В неподвижной (инерциальной) системе отсчета К частица также движется по окружности, но ее линейная скорость равна
. В неподвижной (инерциальной) системе отсчета К частица также движется по окружности, но ее линейная скорость равна
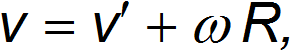
где  — угловая скорость вращающейся системы,
— угловая скорость вращающейся системы, 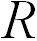 — радиус окружности. Для того, чтобы частица двигалась относительно неподвижной системы отсчета K по окружности со скоростью
— радиус окружности. Для того, чтобы частица двигалась относительно неподвижной системы отсчета K по окружности со скоростью 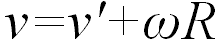 , на нее должна действовать направленная к центру окружности сила
, на нее должна действовать направленная к центру окружности сила 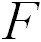 (например, натяжение нити), причем величина этой силы равна
(например, натяжение нити), причем величина этой силы равна
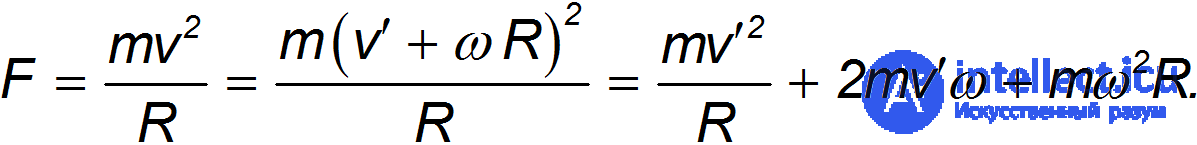
Относительно вращающейся системы отсчета K' в этом случае частица движется с ускорением
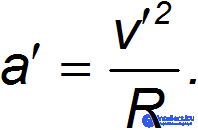
Из полученного выше уравнения второго закона Ньютона для частицы получаем:
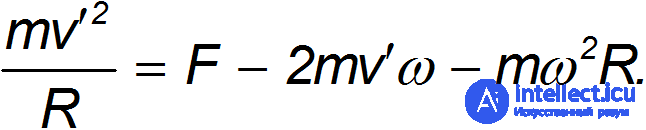
Слева стоит произведение массы на ускорение частицы во вращающейся системе отсчета. Значит, справа должны стоять силы, на нее действующие. Первое слагаемое понятно: это сила натяжения нити, которая одинакова как для инерциальной, так и для неинерциальной систем. С третьим слагаемым мы тоже уже имели дело: это направленная по радиусу (от центра) центробежная сила инерции. Второе слагаемое и есть сила Кориолиса. В данном случае она также направлена от центра, но зависит от скорости частицы. Модуль кориолисовой силы в этом примере равен 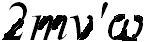 . Ее направление совпадает с движением штопора, ручка которого поворачивается от вектора скорости
. Ее направление совпадает с движением штопора, ручка которого поворачивается от вектора скорости 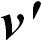 к вектору угловой скорости
к вектору угловой скорости  .
.
Можно показать, что в общем случае сила Кориолиса определяется как
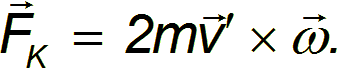
Сила Кориолиса ортогональна вектору скорости. В случае радиального движения, показанного на рис. 8.5, она отклоняла шарик направо, вынуждая его двигаться по траектории 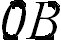 .
.
Возникновение силы Кориолиса при движении тела относительно вращающейся системы отсчета демонстрируется в опыте на рис. 8.6.
Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Приведем некоторые примеры.
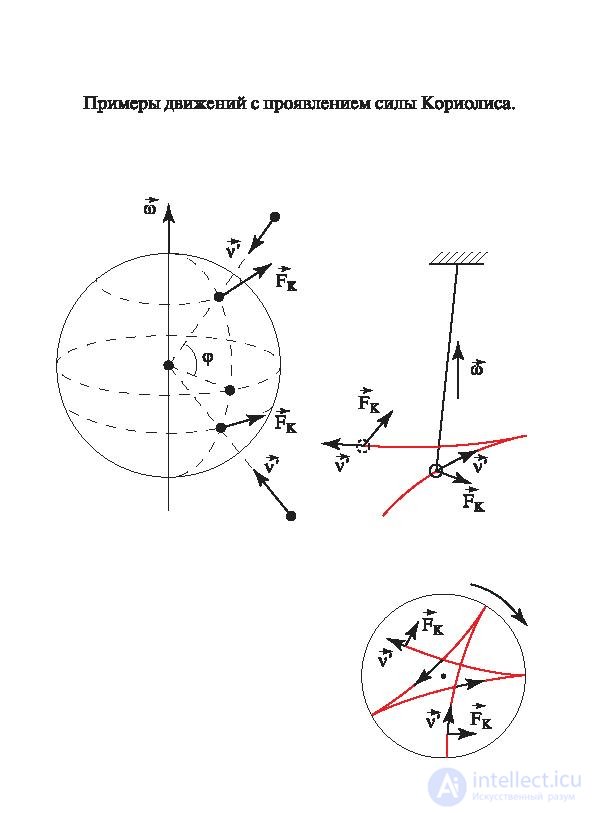
Рис. 8.8. Сила Кориолиса на поверхности Земного шара
В северном полушарии наблюдается более сильное подмывание правых берегов рек, правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, а циклоны вращаются по часовой стрелке. В южном же полушарии все происходит наоборот.
При выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу — в южном (рис. 8.9).
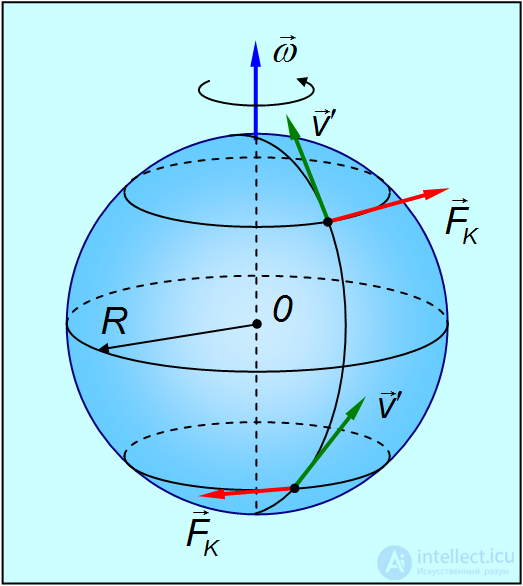
Рис. 8.9. На Земле движущиеся тела отклоняются направо в северном полушарии, и налево в южном
При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к земле, если выстрел произведен на запад, и поднимать его кверху, если выстрел произведен в восточном направлении.
Видео 8.9. Сила Кориолиса: попробуй, попади! Стрельба на вращающейся платформе.
Пример. Поезд массой  = 150 тонн идет в меридиональном направлении на север со скоростью
= 150 тонн идет в меридиональном направлении на север со скоростью 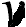 = 72 км/ч. Найдем, чему равна кориолисова сила, прижимающая его в боковом направлении к рельсам, и определим, каков эффект действия центробежной силы. Поезд находится на широте Москвы
= 72 км/ч. Найдем, чему равна кориолисова сила, прижимающая его в боковом направлении к рельсам, и определим, каков эффект действия центробежной силы. Поезд находится на широте Москвы 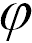 = 56°.
= 56°.
Угол между вектором угловой скорости суточного вращения Земли и касательной к меридиану равен широте места (рис. 8.10).
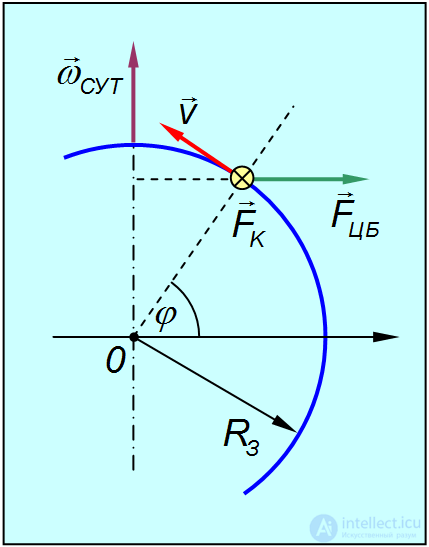
Рис. 8.10. Кориолисова сила направлена от нас перпендикулярно плоскости рисунка
Поэтому кориолисова сила равна
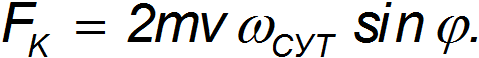
Подставляя числовые данные, находим

Эта сила соответствует весу массы
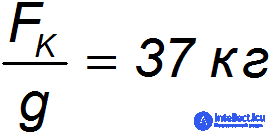
и составляет 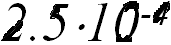 от веса поезда.
от веса поезда.
Расстояние поезда от оси вращения Земли равно 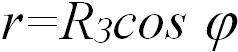 , так что центробежная сила будет
, так что центробежная сила будет
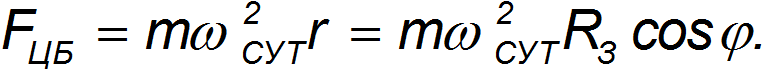
Направлена она по перпендикуляру к оси вращения. Следовательно, ее составляющая
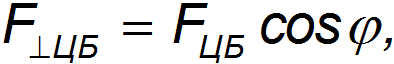
направленная вдоль радиуса Земли, уменьшает вес поезда:
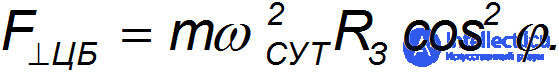
Подставляя числовые данные, получаем
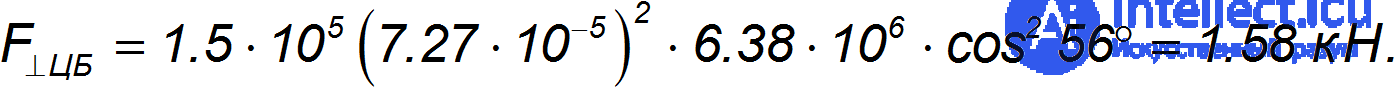
Это соответствует весу массы
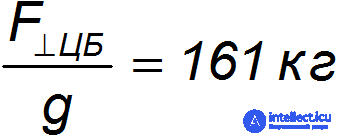
и составляет 1,1·10–3 от веса поезда.
Другая составляющая центробежной силы
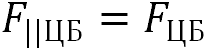
направлена по касательной к меридиану и тормозит поезд. Она равна
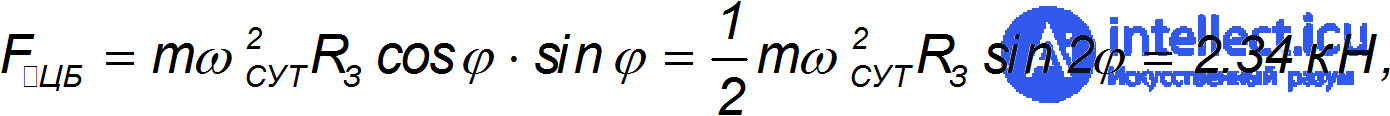
что соответствует весу массы
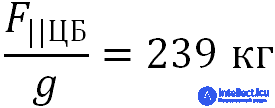
и составляет 1,6·10–3 от веса поезда.
Таким образом, влияние центробежной силы проявляется в десятых долях процента, а проявления кориолисовой силы — на порядок меньше (что связано, разумеется, с небольшой скоростью поезда).
Французский физик Фуко экспериментально доказал вращение Земли вокруг своей оси с помощью 67-метрового маятника, подвешенного к вершине купола парижского Пантеона. Подобный маятник до недавнего времени можно было увидеть в Петербурге в Исаакиевском соборе.

Рис. 8.11. маятник фуко
Колебания маятника Фуко зависят от того, как они были возбуждены. Если маятник отклонить на максимальный угол, а затем отпустить его без начальной скорости, то маятник будет колебаться, как изображено на рис. 10. Скорость движения маятника в положении максимального отклонения будет равна нулю.
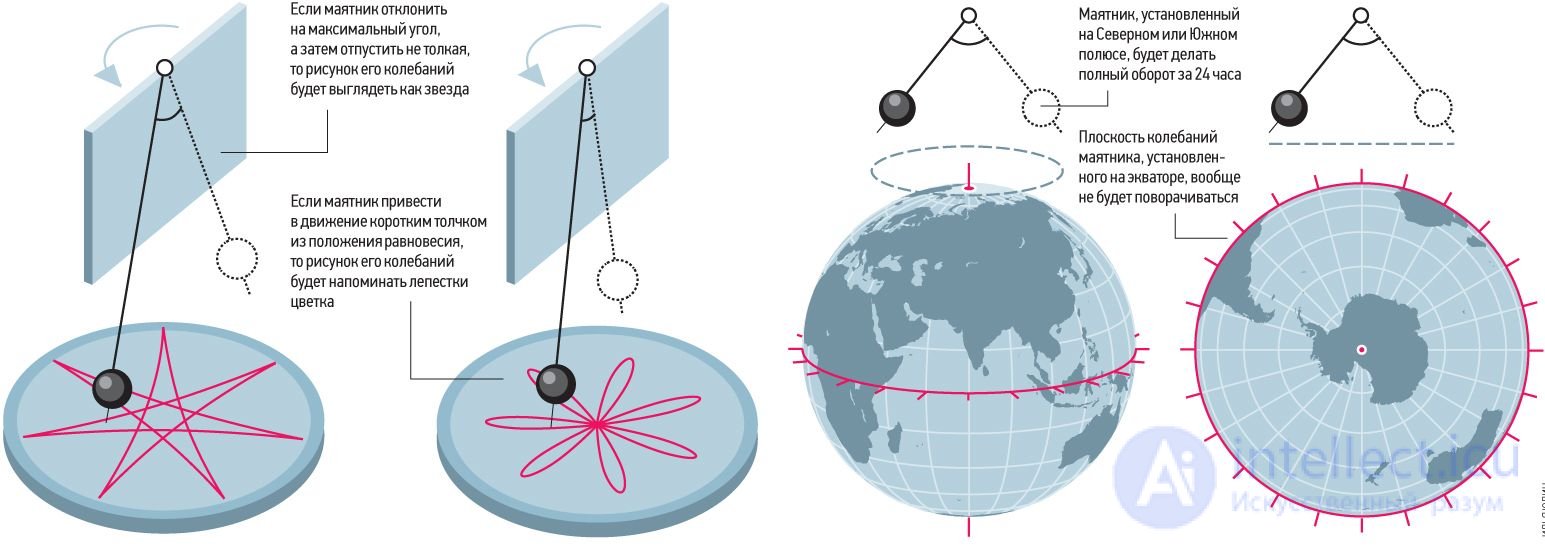
Рис. 8.12. Колебания маятника Фуко при отклонении на максимальный угол и отпускании без начальной скорости
Рис. 8.13. Колебания маятника Фуко при сообщении ему скорости при отклонении на максимальный угол
Несколько иной характер траектории получится, если маятник приводится в движение коротким толчком из положения равновесия. Этому случаю соответствует рис. 8.11. и 8.13. Скорость маятника в положении максимального отклонения соответствует скорости вращения Земли на широте наблюдения.

Исследование, описанное в статье про неинерциальные системы отсчета, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое неинерциальные системы отсчета, силы инерции, сила кориолиса, маятник фуко и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики