Лекция
Привет, сегодня поговорим про нечеткая логика нечеткие множества, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое нечеткая логика нечеткие множества, нечеткие вычисления , настоятельно рекомендую прочитать все из категории Вычислительный интеллект.
Нечеткая логика — это раздел многозначной логики (см. Логики многозначные), который базируется на обобщении классической логики (см. Логика) и теории нечетких множеств, предложенной американским математиком Лютфи (Лотфи) Заде (Lotfi A. Zadeh) для формализации нечетких знаний, характеризуемых лингвистической неопределенностью. Основы теории нечетких множеств были заложены в работе Л. Заде «Fuzzy Sets», опубликованной в 1965 году в журнале «Information and Control» (Zadeh L. A. Fuzzy Sets. — Information and Control, 1965, Vol. 8, № 3, pp. 338–353). Он же дал и название для новой области исследований — «нечеткая логика» (Fuzzy Logic). Предметом нечеткой логики считается исследование рассуждений в условиях нечеткости, размытости, неопределенности, сходных с рассуждениями в обычном смысле. В настоящее время нечеткая логика широко применяется в вычислительных и информационных системах различного назначения, так как она оказалась незаменимой в тех случаях, когда на поставленные вопросы не возможно получить четкие ответы или наперед неизвестны все возможные ситуации.
Под нечетким множеством понимают множество с нечеткими границами, когда переход от принадлежности элементов множеству к непринадлежности их множеству четко не определен. В классической логике элемент x из соответствующей предметной области принадлежит или не принадлежит некоторому множеству М. Характеристическая функция принадлежности элемента множеству принимает лишь два значения: 1, когда x действительно принадлежит М, и 0, когда x не принадлежит множеству М. Например: какая-либо геометрическая фигура либо принадлежит множеству треугольников, либо не принадлежит ему. С нечетким множеством дело обстоит иначе. Здесь элемент x принадлежит множеству A (где A — нечеткое множество) лишь с известной степенью, поэтому функция принадлежности элемента множеству может принимать любые значения в интервале [0, 1], а не только значения 0 или 1.
Согласно Л. Заде, классическое понятие функции принадлежности элемента множеству является недостаточным для рассмотрения ситуаций, которые описываются с помощью нечетко определенных понятий типа «очень истинно», «более-менее истинно», «не очень ложно» и тому подобных. Подобные лингвистические значения представляются нечеткими множествами. Здесь дихотомия рассмотренной функции принадлежности не позволяет любому элементу или принадлежать, или не принадлежать данному множеству. Таким образом, дихотомия функции принадлежности должна быть отвергнута точно так же, как в многозначных логиках отвергается дихотомия функции приписывания истинностных значений (принцип двузначности). Тогда, следуя логике Л. Заде, в основе теории нечетких множеств лежит представление о том, что составляющие множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно, принадлежать данному множеству с различной степенью. При таком подходе высказывание типа «элемент принадлежит данному множеству A» теряет смысл, поскольку следует указать, с какой степенью элемент принадлежит данному множеству. Обычно это множество степеней принадлежности оценивается на бесконечной шкале действительных чисел от 0 до 1, то есть на интервале [0, 1], который используется как универсальное множество для задания лингвистической переменной «истинность». В целом, это позволяет определить промежуточные значения для таких общепринятых выражений, как да|нет, истинно|ложно, черное|белое и тому подобных. Таким образом, выражения нечетко определенных понятий стало возможно формулировать математически. Затем над множеством нечетких [под]множеств определяются простейшие логические операции пересечения «∩», объединения «∪» и дополнения «¯».
В 1973 году Л. Заде вводит понятие такой нечеткой логики, в которой множеством истинностных значений является счетное множество лингвистических названий значений истинности, понимаемой как лингвистическая переменная, в качестве значений которой выступают нечеткие множества, то есть такая переменная, значениями которой являются слова или предложения естественного или искусственного языка. Множество допустимых значений лингвистической переменной называется терм-множеством. В свою очередь, лингвистические значения истинности имеют числовые значения, в качестве которых уже выступают нечеткие множества, то есть понятие истинности само является нечетким, в отличие от классической логики, где истинность может принимать только два значения: «истинно» и «ложно». Понятие лингвистической переменной играет важную роль в нечетком логическом выводе и в принятии решений на основе приближенных рассуждений.
Формально, нечеткая и лингвистическая переменные определяются следующим образом.
Нечеткая переменная характеризуется набором-тройкой 〈 a, X, A〉, где:
Лингвистическая переменная характеризуется набором-пятеркой 〈 b, T, X, G, M〉, где:
Использование символов:
К настоящему времени сложились два основных направления исследований в нечеткой логике.
Первое направление включает нечеткую логику в широком смысле, под которой зачастую понимается все, что связано с нечеткими множествами. Начиная с 1970-х годов теория нечетких множеств приобрела значительную популярность. С 1970 года начал выходить международный журнал «Fuzzy Sets and Systems». С конца 1980-х годов нечеткая логика занимает одно из ведущих положений в информационных технологиях. Поскольку нечеткая логика оказалась весьма пригодной для работы с аппроксимированной информацией, она применяется для управления нелинейными системами и для моделирования сложных систем, где неясность и неопределенность общеприняты. Сегодня нечеткая логика заложена в различные управляющие, информационные, электронные и многие другие системы, включая системы искусственного интеллекта. Эффективное моделирование приближенных рассуждений нашло важное применение для решения сложных задач программирования и вообще в технологии так называемых «мягких вычислений» (Soft Computing). К настоящему времени опубликованная литература, посвященная проблематике нечетких множеств, насчитывает уже свыше 10 тысяч работ.
Второе направление включает нечеткую логику в узком смысле, использующую методы символической логики (см. Логика символическая): семантика, синтаксис, аксиоматизация, дедукция, полнота и другие — как для логики высказываний (см. Об этом говорит сайт https://intellect.icu . Логика высказываний), так и для логики предикатов (см. Логика предикатов). В этом русле нечеткая логика разрабатывается как раздел многозначной логики. Это направление является относительно молодой дисциплиной, исследующей новые логические исчисления с далеко идущими перспективами.
Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.
Прежде чем нечеткий подход к моделированию сложных систем получил признание во всем мире, прошло не одно десятилетие с момента зарождения теории нечетких множеств. И на этом пути развития нечетких систем принято выделять три периода.
Первый период (конец 60-х–начало 70 гг.) характеризуется развитием теоретического аппарата нечетких множеств (Л. Заде, Э. Мамдани, Беллман). Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением). Одновременно стало уделяться внимание вопросам построения экспертных систем, построенных на нечеткой логике, разработке нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике. Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.
Триумфальное шествие нечеткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy Approximation Theorem). В бизнесе и финансах нечеткая логика получила признание после того как в 1988 году экспертная система на основе нечетких правил для прогнозирования финансовых индикаторов единственная предсказала биржевой крах. И количество успешных фаззи-применений в настоящее время исчисляется тысячами.
Характеристикой нечеткого множества выступает функция принадлежности (Membership Function). Обозначим через MFc(x) – степень принадлежности к нечеткому множеству C, представляющей собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C={MFc(x)/x}, MFc(x) [0,1]. Значение MFc(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.
Проиллюстрируем это на простом примере. Формализуем неточное определение "горячий чай". В качестве x (область рассуждений) будет выступать шкала температуры в градусах Цельсия. Очевидно, что она будет изменяется от 0 до 100 градусов. Нечеткое множество для понятия "горячий чай" может выглядеть следующим образом:
C={0/0; 0/10; 0/20; 0,15/30; 0,30/40; 0,60/50; 0,80/60; 0,90/70; 1/80; 1/90; 1/100}.
Так, чай с температурой 60 С принадлежит к множеству "Горячий" со степенью принадлежности 0,80. Для одного человека чай при температуре 60 С может оказаться горячим, для другого – не слишком горячим. Именно в этом и проявляется нечеткость задания соответствующего множества.
Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов, являются пересечение и объединение.
Пересечение двух нечетких множеств (нечеткое "И"): A B: MFAB(x)=min(MFA(x), MFB(x)).
Объединение двух нечетких множеств (нечеткое "ИЛИ"): A B: MFAB(x)=max(MFA(x), MFB(x)).
В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в так называемых треугольных нормах и конормах. Приведенные выше реализации операций пересечения и объединения – наиболее распространенные случаи t-нормы и t-конормы.
Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных.
Нечеткая переменная описывается набором (N,X,A), где N – это название переменной, X – универсальное множество (область рассуждений), A – нечеткое множество на X.
Значениями лингвистической переменной могут быть нечеткие переменные, т.е. лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная. Каждая лингвистическая переменная состоит из:
Рассмотрим такое нечеткое понятие как "Цена акции". Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество, которое будет состоять из трех нечетких переменных: "Низкая", "Умеренная", "Высокая" и зададим область рассуждений в виде X=[100;200] (единиц). Последнее, что осталось сделать – построить функции принадлежности для каждого лингвистического терма из базового терм-множества T.
Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и гауссова функции принадлежности.
Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:
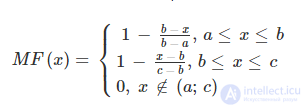
При (b-a)=(c-b) имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a,b,c).
Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):
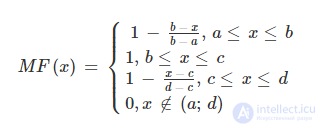
При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
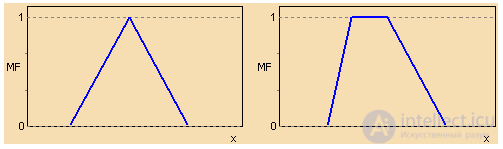
Рисунок 1. Типовые кусочно-линейные функции принадлежности
Функция принадлежности гауссова типа описывается формулой
MF(x)=exp[−(x−cσ)2]MF(x)=exp[−(x−cσ)2]
и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр отвечает за крутизну функции.

Рисунок 2. Гауссова функция принадлежности
Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображаются вместе на одном графике. На рисунке 3 приведен пример описанной выше лингвистической переменной "Цена акции", на рисунке 4 – формализация неточного понятия "Возраст человека". Так, для человека 48 лет степень принадлежности к множеству "Молодой" равна 0, "Средний" – 0,47, "Выше среднего" – 0,20.
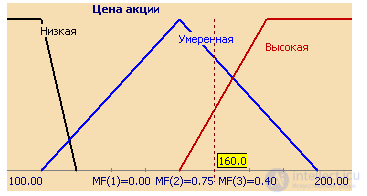
Рисунок 3. Описание лингвистической переменной "Цена акции"
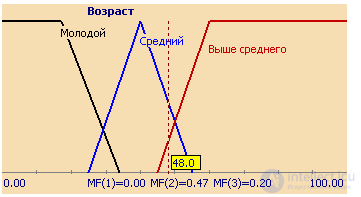
Рисунок 4. Описание лингвистической переменной "Возраст"
Количество термов в лингвистической переменной редко превышает 7.
Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме "Если-то" и функции принадлежности для соответствующих лингвистических термов. При этом должны соблюдаться следующие условия:
В противном случае имеет место неполная база нечетких правил.
Пусть в базе правил имеется m правил вида:
R1: ЕСЛИ x1 это A11 … И … xn это A1n, ТО y это B1
…
Ri: ЕСЛИ x1 это Ai1 … И … xn это Ain, ТО y это Bi
…
Rm: ЕСЛИ x1 это Ai1 … И … xn это Amn, ТО y это Bm,
где xk , k=1..n – входные переменные; y – выходная переменная; Aik – заданные нечеткие множества с функциями принадлежности.
Результатом нечеткого вывода является четкое значение переменной y* на основе заданных четких значений xk , k=1..n.
В общем случае механизм логического вывода включает четыре этапа: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация (см. рисунок 5).
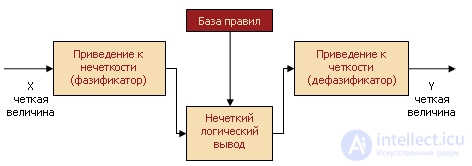
Рисунок 5. Система нечеткого логического вывода
Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото.
Рассмотрим подробнее нечеткий вывод на примере механизма Мамдани (Mamdani). Это наиболее распространенный способ логического вывода в нечетких системах. В нем используется минимаксная композиция нечетких множеств. Данный механизм включает в себя следующую последовательность действий.
Нечеткий вывод. Сначала определяются уровни "отсечения" для левой части каждого из правил:
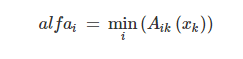
Далее находятся "усеченные" функции принадлежности:
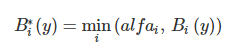
Композиция, или объединение полученных усеченных функций, для чего используется максимальная композиция нечетких множеств:
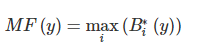
где MF(y) – функция принадлежности итогового нечеткого множества.
Дефазификация, или приведение к четкости. Существует несколько методов дефазификации. Например, метод среднего центра, или центроидный метод:
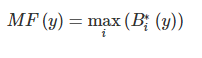
Геометрический смысл такого значения – центр тяжести для кривой MF(y). Рисунок 6 графически показывает процесс нечеткого вывода по Мамдани для двух входных переменных и двух нечетких правил R1 и R2.

Рисунок 6. Схема нечеткого вывода по Мамдани
Гибридизация методов интеллектуальной обработки информации – девиз, под которым прошли 90-е годы у западных и американских исследователей. В результате объединения нескольких технологий искусственного интеллекта появился специальный термин – "мягкие вычисления" (soft computing), который ввел Л. Заде в 1994 году. В настоящее время мягкие вычисления объединяют такие области как: нечеткая логика, искусственные нейронные сети, вероятностные рассуждения и эволюционные алгоритмы. Они дополняют друг друга и используются в различных комбинациях для создания гибридных интеллектуальных систем.
Влияние нечеткой логики оказалось, пожалуй, самым обширным. Подобно тому, как нечеткие множества расширили рамки классической математическую теорию множеств, нечеткая логика "вторглась" практически в большинство методов Data Mining, наделив их новой функциональностью. Ниже приводятся наиболее интересные примеры таких объединений.
Нечеткие нейронные сети (fuzzy-neural networks) осуществляют выводы на основе аппарата нечеткой логики, однако параметры функций принадлежности настраиваются с использованием алгоритмов обучения НС. Поэтому для подбора параметров таких сетей применим метод обратного распространения ошибки, изначально предложенный для обучения многослойного персептрона. Для этого модуль нечеткого управления представляется в форме многослойной сети. Нечеткая нейронная сеть как правило состоит из четырех слоев: слоя фазификации входных переменных, слоя агрегирования значений активации условия, слоя агрегирования нечетких правил и выходного слоя.
Наибольшее распространение в настоящее время получили архитектуры нечеткой НС вида ANFIS и TSK. Доказано, что такие сети являются универсальными аппроксиматорами.
Быстрые алгоритмы обучения и интерпретируемость накопленных знаний – эти факторы сделали сегодня нечеткие нейронные сети одним из самых перспективных и эффективных инструментов мягких вычислений.
Классические нечеткие системы обладают тем недостатком, что для формулирования правил и функций принадлежности необходимо привлекать экспертов той или иной предметной области, что не всегда удается обеспечить. Адаптивные нечеткие системы (adaptive fuzzy systems) решают эту проблему. В таких системах подбор параметров нечеткой системы производится в процессе обучения на экспериментальных данных. Алгоритмы обучения адаптивных нечетких систем относительно трудоемки и сложны по сравнению с алгоритмами обучения нейронных сетей, и, как правило, состоят из двух стадий: 1. Генерация лингвистических правил; 2. Корректировка функций принадлежности. Первая задача относится к задаче переборного типа, вторая – к оптимизации в непрерывных пространствах. При этом возникает определенное противоречие: для генерации нечетких правил необходимы функции принадлежности, а для проведения нечеткого вывода – правила. Кроме того, при автоматической генерации нечетких правил необходимо обеспечить их полноту и непротиворечивость.
Значительная часть методов обучения нечетких систем использует генетические алгоритмы. В англоязычной литературе этому соответствует специальный термин – Genetic Fuzzy Systems.
Значительный вклад в развитие теории и практики нечетких систем с эволюционной адаптацией внесла группа испанских исследователей во главе с Ф. Херрера (F. Herrera).
Нечеткие запросы к базам данных (fuzzy queries) – перспективное направление в современных системах обработки информации. Данный инструмент дает возможность формулировать запросы на естественном языке, например: "Вывести список недорогих предложений о съеме жилья близко к центру города", что невозможно при использовании стандартного механизма запросов. Для этой цели разработана нечеткая реляционная алгебра и специальные расширения языков SQL для нечетких запросов. Большая часть исследований в этой области принадлежит западноевропейским ученым Д. Дюбуа и Г. Праде.
Нечеткие ассоциативные правила (fuzzy associative rules) – инструмент для извлечения из баз данных закономерностей, которые формулируются в виде лингвистических высказываний. Здесь введены специальные понятия нечеткой транзакции, поддержки и достоверности нечеткого ассоциативного правила.
Нечеткие когнитивные карты (fuzzy cognitive maps) были предложены Б. Коско в 1986 г. и используются для моделирования причинных взаимосвязей, выявленных между концептами некоторой области. В отличие от простых когнитивных карт, нечеткие когнитивные карты представляют собой нечеткий ориентированный граф, узлы которого являются нечеткими множествами. Направленные ребра графа не только отражают причинно-следственные связи между концептами, но и определяют степень влияния (вес) связываемых концептов. Активное использование нечетких когнитивных карт в качестве средства моделирования систем обусловлено возможностью наглядного представления анализируемой системы и легкостью интерпретации причинно-следственных связей между концептами. Основные проблемы связаны с процессом построения когнитивной карты, который не поддается формализации. Кроме того, необходимо доказать, что построенная когнитивная карта адекватна реальной моделируемой системе. Для решения данных проблем разработаны алгоритмы автоматического построения когнитивных карт на основе выборки данных.
Нечеткие методы кластеризации, в отличие от четких методов (например, нейронные сети Кохонена), позволяют одному и тому же объекту принадлежать одновременно нескольким кластерам, но с различной степенью. Нечеткая кластеризация во многих ситуациях более "естественна", чем четкая, например, для объектов, расположенных на границе кластеров. Наиболее распространены: алгоритм нечеткой самоорганизации c-means и его обобщение в виде алгоритма Густафсона-Кесселя.
Список можно продолжить и дальше: нечеткие деревья решений, нечеткие сети Петри, нечеткая ассоциативная память, нечеткие самоорганизующиеся карты и другие гибридные методы.
ЛИТЕРАТУРА
К сожалению, в одной статье не просто дать все знания про нечеткая логика нечеткие множества. Но я - старался. Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое нечеткая логика нечеткие множества, нечеткие вычисления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Вычислительный интеллект
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Вычислительный интеллект
Термины: Вычислительный интеллект