Лекция
Привет, Вы узнаете о том , что такое иерархические данные, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое иерархические данные, adjacency list, список смежных вершин, nested set, вложенное множество, materialized path, материализованный путь , настоятельно рекомендую прочитать все из категории MySql (Maria DB).
Большинство программистов в тот или иной момент столкнулись с построением иерархической информации в базе данных SQL и, поняли, что управление иерархическими данными – это явно не предназначение реляционной базы данных. Таблицы реляционных баз данных являются не иерархическими (похожими на XML), а простыми плоскими списками.
иерархические данные имеют отношения родитель-ребенок, которые, естественно, не представлены в таблице реляционной базы данных.
Стандартная реляционная алгебра и реляционное исчисление, а также операции SQL, основанные на них, не могут напрямую выразить все желаемые операции над иерархиями. Вложенная модель множества является решением этой проблемы.
Альтернативным решением является выражение иерархии как отношения родитель-потомок. Селко назвал это списком смежности. Если иерархия может иметь произвольную глубину, то список смежности не допускает выражения операций, как сравнение содержимого иерархий двух элементов или определение того, находится ли элемент где-то в подиерархии другого элемента. Когда иерархия имеет фиксированную или ограниченную глубину, операции возможны, но дорогостоящие, из-за необходимости выполнения на каждом уровне одного реляционного соединения. Это часто называют проблемой спецификации материалов .
Иерархии могут быть легко выражены путем переключения на графовую базу данных. В качестве альтернативы, существует несколько решений для реляционной модели, которые доступны в качестве обходного пути в некоторых системах управления реляционными базами данных:
Когда эти решения недоступны или неосуществимы, необходимо использовать другой подход.
В реляционных базах данных хранение информации в виде древовидных структур является задачей с дополнительными накладными расходами. Такими дополнительными расходами могут быть как, увеличение количества запросов, так и увеличение количества информации, которая служит для организации структуры данных.
Распространенными подходами для организации древовидных структур являются:
|
Adjacency List |
Организация структуры данных заключается в том, что каждый объект хранит информацию о родительском объекте, то есть в строке таблицы имеется дополнительное поле, в котором указывается ID объекта, в который вложен данный объект.
|
| Nested Set вложенное множество |
Вложенные множества хранят информацию не Только о так называемых левом и правом ключе, а также уровне вложенности. Данный вариант организации структуры данных удобен для чтения, но более тяжело поддается модификации. |
| Materialized Path материализованный путь |
Идея этой структуры данных заключается в том, что каждая запись хранит полный путь к корневому элементу дерева. |
Рассмотрение этих структур данных было вызвано необходимостью внедрения на сайт поддержки комментариев(с древовидной структурой) для статей.
Adjacency List несколько неудобное решение для организации комментариев, поскольку могут быть проблемы с нахождением родительских объектов и выстраиванием древовидной структуры, хотя сам по себе подход позволяет довольно быстро удалять и добавлять элементы.
Nested Set довольно громоздкий метод для организации комментариев на небольшом сайте, да если даже посмотреть в сторону крупных ресурсов, то там под статьями не так уж часто бывает по 5000 комментариев. Также меня смутил тот факт, что необходимо будет добавлять скрываемый root элемент, так называемый первый пустой комментарий в статье, от которого будет строится все дерево. Зачем плодить лишние сущности? - Хотя может я и ошибаюсь. Ну и последним аргументом "против" стала необходимость пересчета ключей при добавлении новых комментариев. В общем, несмотря на преимущества данной структуры, в рамках данного сайта и его текущего состояния - этот путь хранения комментариев станет стрельбой из пушки по воробьям.
Materialized Path - Каждый комментарий содержит полный путь. И при этом под статьей может организовываться несколько деревьев комментариев. То есть любой комментарий, который находится на первом уровне, автоматически считается корневым для своего дерева. А при добавлении нового комментария необходимо взять полный путь из будущего родителя и прибавить к нему только лишь ID нового комментария. при выборке деревьев комментариев можно выполнять сортировку по данным массивам, что автоматически позволит располагать все комментарии в хронологическом порядке с сохранением структуры дерева
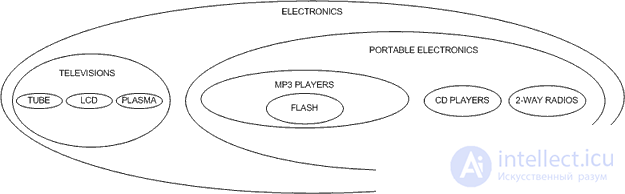
В нашем примере, иерархические данные представляет собой набор элементов, в которой каждый элемент имеет одного родителя и ноль или более детей (за исключением корневого элемента, который не имеет родителей). Иерархические данные можно найти в самых разных приложениях баз данных, включая форумы и темы рассылки, схемы организации бизнеса, управления категориями контента, и категориями продукции. Для нашего примера мы будем использовать следующую иерархию категорий продуктов из вымышленного магазина электроники:

Mysql до 8.0 версии возможно хранение иерархических данных в виде вложенных моржеств , модели списка соседей. Начиная с 8.0 версии MYSQL возможна работа с табличнымми выражениями для обработки и хранения иерархических данных



Эти категории образуют иерархию, подобно примерам, приведенным выше. В этой статье мы рассмотрим две модели для работы с иерархическими данными в MySQL, начиная с традиционной моделью список смежности (Adjacency List Model).
Модель Список смежности (Adjacency List Model)
Как правило, примеры указанные выше, будут храниться в таблице с следующим определением (я включаю в пример все выражения CREATE и INSERT, чтобы мы смогли следить вместе за ходом мысли):
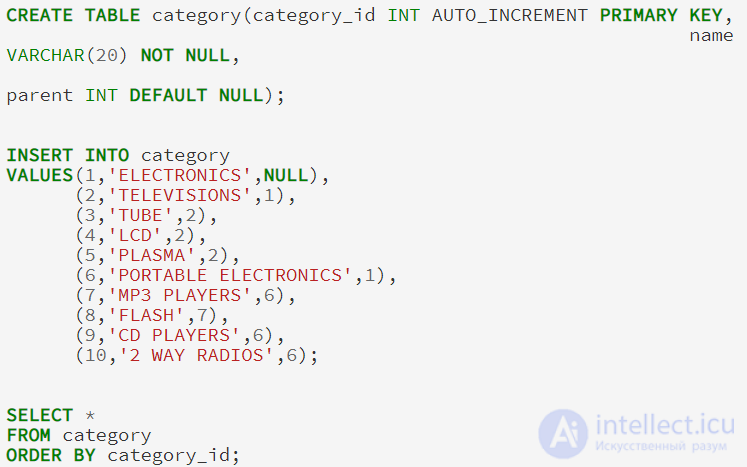
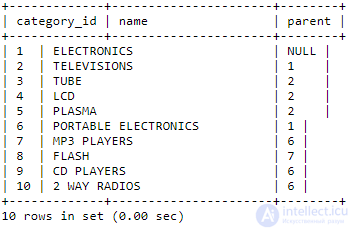
В модели списка смежности, каждый элемент таблицы содержит указатель на его родителя. Самый верхний элемент, в данном случае ELECTRONICS, имеет значение NULL для его родителей. Модель список смежности имеет преимущество, довольно легко можно увидеть, что FLASH является дочерним MP3 PLAYERS, который является дочерним для портативной электроники, который является дочерним электроники. В то время как модель списка смежности довольно легка в реализации, может возникнуть проблема при реализации на SQL.
Получение полного дерева
Первая общая задача при работе с иерархическими данными является отображение всего дерева, как правило, с разной глубиной. Наиболее распространенным способом для этого является в чистом SQL, с помощью объединения таблиц:


Просмотр всех узлов лист
Мы можем найти все конечные узлы в дереве (т.е. без детей) с помощью
LEFT JOIN, запрос:


Получение одного пути
Объединение также позволяет нам увидеть полный путь нашей иерархии:

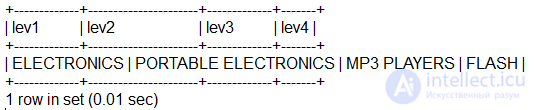
Основным ограничением такого подхода является то, что вам нужно объединение для каждого уровня в иерархии, и производительность будет существенно ухудшаться с каждым добавляемым уровнем, будет расти сложность.
Ограничения Примерного Списка смежности
Работа с моделью список смежности в чистом SQL может быть затруднена в лучшем случае. Перед тем как увидеть полный путь к категории мы должны знать, на каком уровне она находится. Кроме того, особое внимание должно быть уделено удалению узлов из-за возможности сиротства всей ветки (удалить категорию портативной электроники категории и всех ее детей-сирот). Некоторые из этих ограничений могут быть решены с помощью клиентского кода или хранимых процедур. С процедурным языком, мы можем начать с нижней части дерева и повторять вверх возврат полного дерева или одного пути. Мы также можем использовать процедурное программирование для удаления узлов всей ветки без сиротства, продвигая один дочерний элемент и изменяя порядок расположения остальных детей, чтобы указать на нового родителя.
Расширенный список смешности (сеседей) в базах данных
иногда добавляют специяальные поля level path в которых содержиться информация об оровне узла и пути к родителям
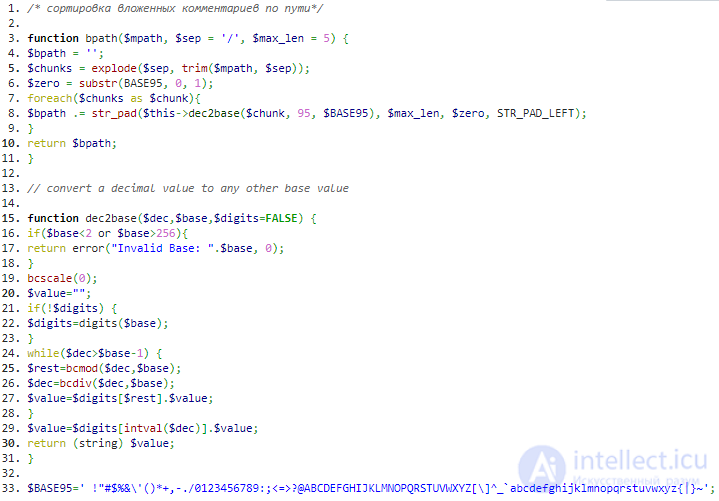
еще одна разновидность хранения списка соседей использование бинарного Materialized Path
Решение проблемы сортировки деревьев с помощью бинарного Materialized Path
использовать не десятичные ID в пути, а кодировать в другую систему счисления, чтобы иметь меньше ограничений
в длине пути. Об этом говорит сайт https://intellect.icu . При этом, разделители в виде точек или других символов не нужны, так как поле будет
использоваться только для сортировки.
можно использовать основание 95, это как раз число печатаемых символов в ASCII.
Если для каждого значения в пути мы будем использовать фиксированную длину, получим следующий верхний порог ID:
1 — 95^1 — 1 = 94
2 — 95^2 — 1 = 9 024
3 — 95^3 — 1 = 857 374
4 — 95^4 — 1 = 81 450 624
5 — 95^5 — 1 = 7 737 809 374
5-ти символов вполне достаточно, чтобы не волноваться о максимальном количестве комментариев.
Максимальный уровень вложенности, при этом, для VARCHAR 255/5 = 51
Теоретически, можно брать не BASE95, а BASE256 (вместе с непечатаемыми символами),
но хранить это все бинарно в BLOB, правда тут я не уверен с производительностью при
сортировке (надо проверить). Тогда уже 3 символами мы могли бы кодировать
16 777 215 вариантов, а 4 — 4 294 967 295.
Модель вложенного множества (англ. Nested set model) — это способ представления вложенных множеств (англ.) (известных как деревья или иерархии) в реляционных базах данных.
Модель вложенного множества состоит в том, чтобы пронумеровать узлы в соответствии с обходом дерева, который дважды посещает каждый узел. При обоих посещениях назначаются номера в порядке посещения. Обход оставляет два числа для каждого узла, которые хранятся в виде двух атрибутов. Запрос становится недорогим: принадлежность к иерархии можно проверить, сравнив эти числа. Обновление узла требует перенумерации дерева и поэтому является дорогостоящим. Улучшения, в которых вместо целых чисел используются рациональные числа, помогут избежать перенумерации и поэтому узлы обновляются быстрее, хоть и намного сложнее .
На чем бы я хотел остановиться в этой статье, так это другой подход, называемый, как правило, модель вложенных множеств (The Nested Set Model). В модели вложенных множеств, мы можем посмотреть на нашу иерархию по-новому, а не как на узлы и линии, а как на вложенные контейнеры. Попробуем нарисовать наши категории электроники следующим образом:
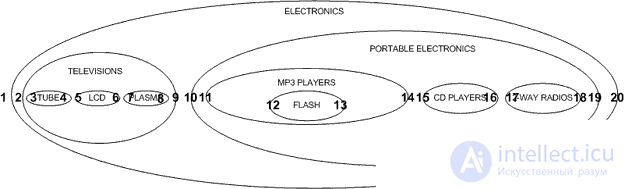
Обратите внимание, что наша иерархия по-прежнему сохраняется, родительские категории сохраняют дочерние. Мы представляем эту форму иерархии в таблице с помощью указателей на левые и правые узлы в наших множествах:

Мы используем lft и rgt, потому что left и right являются зарезервированными словами MySQL
см. http://dev.mysql.com/doc/mysql/en/reserved-words.html полный список зарезервированных слов.
Так как же нам определить левое и правое значения? Мы начинаем нумерацию с левой стороны внешних узлов и продолжать вправо:
Эта конструкция может быть представлена типичным деревом, как на изображении:
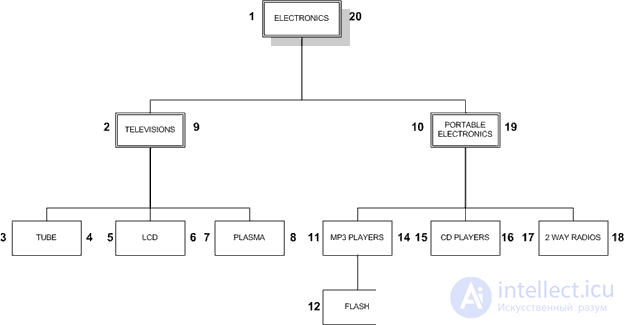
При работе с деревом, мы работаем слева направо, один слой за один другим, спускаясь на детей каждого узла, прежде чем присвоим rgt и перейдем на право. Такой подход называется изменениеалгоритмом прямого обхода дерева (preorder tree traversal algorithm).
Получение полного дерева
Мы можем получить полное дерево с помощью объединения, которое связывает родителей с узлами на основании, что lft значение узла будет всегда появляться между lft своих родителей и значением rgt:

В отличие от нашего предыдущего примера с моделью список смежности, этот запрос будет работать независимо от глубины дерева. Мы не касаемся со значением rgt узла в нашем предикате BETWEEN, так как значение rgt всегда подпадают под те же родители, что и lft значения.
Нахождение всех конечных узлов
Нахождение всех конечных узлов в модели вложенных множеств даже проще, чем LEFT JOIN метод используемый в модели списка смежности. Если вы посмотрите на таблицу nested_category, вы можете заметить, что LFT и RGT значения для конечных узлов являются последовательными числами. Чтобы найти конечных узлов, мы ищем узлы, где rgt = lft+ 1:
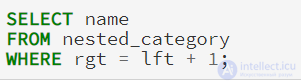

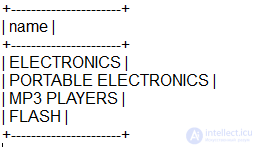
Получение одного путь
При модель вложенных множеств, мы можем получить один путь, не образуя несколько объединений таблиц:
Определение глубины узлов
Мы уже рассмотрели, как показывают все дерево целиком, но что, если мы хотим также показать глубину каждого узла в дереве, чтобы лучше определить, как каждый узел размещается в иерархии? Это может быть сделано путем добавления функции COUNT и предиката (клауза) GROUP BY для наших существующих запросов для отображения всего дерева:


Мы можем использовать значение глубины для формирования отступов с у наших категорий с помощью строковых функций CONCAT и REPEAT


Конечно, в клиентском приложении, вы будете чаще использовать значение глубины непосредственно для отображения иерархии. Веб-разработчики могут повторять цикл по дереву, добавив теги и по мере увеличения размера глубины и уменьшения.
Глубина поддерева (ветки)
Когда нам нужна подробная информация о ветке, мы не можем ограничить узел или родительские таблицы в нашем объединении (self-join), потому что это испортит наши результаты. Вместо этого, мы добавим третье объединение, а также подзапрос, чтобы определить глубину, которая будет новой точкой отсчета для нашей ветки:
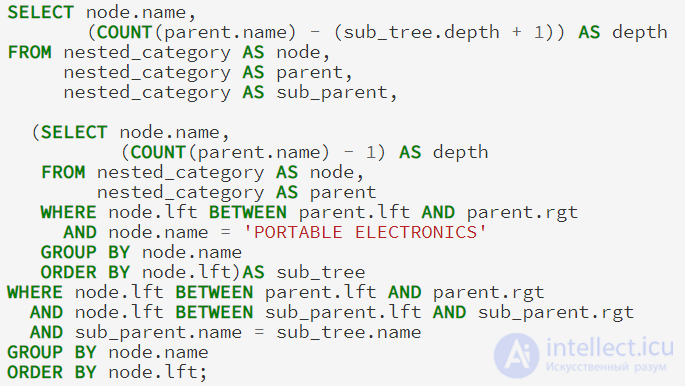
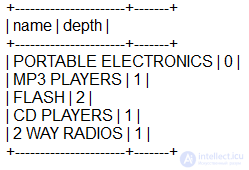
Эта функция может быть использована с любым именем узла, в том числе с корневым узлом .Значения глубины всегда по отношению к имени узла.
Нахождение непосредственных подчиненных узлов
Представьте, что вы показываете категории продуктов электроники на веб-сайте продавца. Когда пользователь щелкает на категории, вы хотите, чтобы отобразились продукты этой категории, а также немедленное были перечислены его подкатегории, но не все дерево категорий под ним. Для этого нам нужно показать, узлы и его непосредственные подузлы, но не ниже по дереву. Например, при показе категории PORTABLE ELECTRONICS, мы хотим показать MP3 PLAYERS, CD PLAYERS и 2 WAY RADIOS, но не FLASH.
Это можно легко сделать путем добавления предложения HAVING в наших предыдущих запросов:
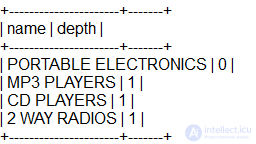
Если вы не хотите, чтобы отображался родительский узел, измените HAVING depth <= 1 на HAVING depth = 1.
Агрегирующие функции во вложенных множествах
Давайте добавим таблицу продуктов, которые мы можем использовать, чтобы продемонстрировать агрегатныe функции:

Теперь давайте выполним запрос, который сможет получить дерево наших категорий, а также количество продуктов по каждой категории:

Это наше типичное целое дерево запроса с добавленными COUNT и GROUP BY, наряду со ссылкой на продукт таблицы и соединением между узлом и продуктами таблицы в предикате WHERE. Как вы видите, есть запись для каждой категории и число подкатегорий содержащихся в родительских категориях.
Добавление новых узлов
Теперь, когда мы узнали, как получить наше дерево, мы должны взглянуть на то, как обновить наше дерево путем добавления новых узлов. Давайте посмотрим на нашу схему модели вложенных множеств снова:
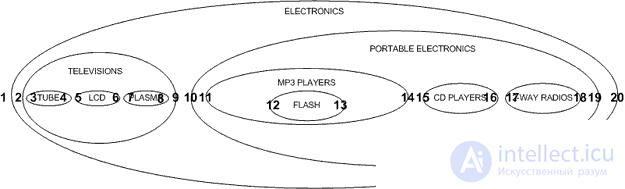
Если мы хотим добавить новый узел между узлами TELEVISIONS и PORTABLE ELECTRONICS, новый узел будет иметь lft и rgt значения 10 и 11, и все его узлы справа будут иметь свои lft и rgt значения увеличена на два. Затем мы добавляем новый узел с соответствующим значениями lft и rgt. Хотя это может быть сделано с помощью хранимых процедур в MySQL 5, я буду считать, что в данный момент большинство читателей используют 4.1, так как это последняя стабильная версия, и я буду изолировать мой запрос с выражением LOCK TABLES:
Мы можем проверить наши вложения с нашими отступом дерева запроса:

Если вместо этого мы хотим добавить узел в качестве дочернего узла, который не имеет существующих детей, мы должны немного изменить наши процедуры. Давайте добавим новый узел FRS ниже узла 2 WAY RADIOS:
Как видите, наш новый узел теперь правильно вложен:

Удаление узлов
Последние основной задачей в работе с вложенными множествами заключается в удалении узлов. Набор ваших действий при удалении узла, зависит от положения узла в иерархии, удаление сделать листьев легче, чем удаление узлов с детьми, потому что мы должны обращаться с сиротами узлов.
При удалении листа узла, в отличие от добавления новых узлов, мы удаляем узел и его ширину от каждого узла правее:
И опять, мы выполняем запрос оформляя отступы в дереве, чтобы подтвердить что наш узел был удален без нарушения иерархии:

Этот подход работает одинаково хорошо при удалении узла и всех его детей:
И опять, мы запрашиваем, чтобы увидеть, успешно ли мы удалили все ветки:

Другой сценарий, который можно использовать при удаление родительского узла, а не детей. В некоторых случаях вы можете просто изменить название заполнителя до замены представлены, например, когда увольняют руководителя. В других случаях, дочерние узлы должны быть подняты до уровня удаленного родителя:
В этом случае мы вычитаем два от всех элементов справа от узла (так как без детей, это будет иметь ширину двух), и один из узлов, которые являются его дети (чтобы закрыть пробел, созданный потерей левой родителей значение). Еще раз, мы можем подтвердить наши элементы были повышены:

Другие сценарии при удалении узлов будут включать содействие одному из детей родители положение и перемещение ребенка узлов под братом родительский узел, но ради пространство этих сценариев не рассматривается в этой статье.
В каталоге магазина одежда может быть классифицирована в соответствии с иерархией, приведенной слева:
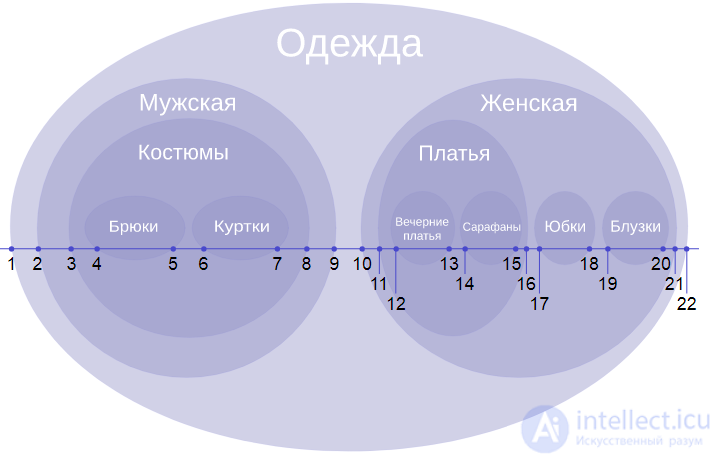
Диаграмма Эйлера категорий одежды
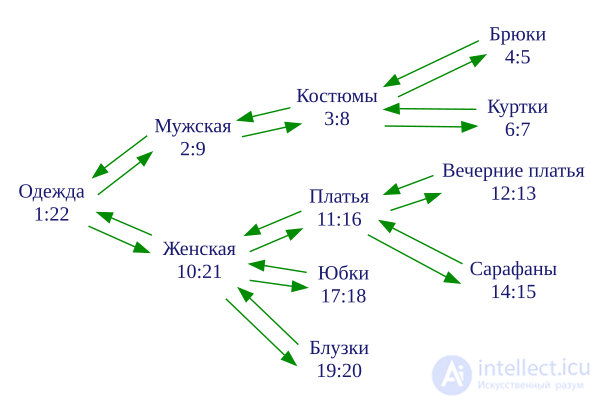
Нумерация, назначаемая обходом дерева
| № п/п | Узел | Левый | Правый |
|---|---|---|---|
| 1 | Одежда | 1 | 22 |
| 2 | Мужская | 2 | 9 |
| 3 | Женская | 10 | 21 |
| 4 | Костюмы | 3 | 8 |
| 5 | Брюки | 4 | 5 |
| 6 | Куртки | 6 | 7 |
| 7 | Платья | 11 | 16 |
| 8 | Юбки | 17 | 18 |
| 9 | Блузки | 19 | 20 |
| 10 | Вечерние платья | 12 | 13 |
| 11 | Сарафаны | 14 | 15 |
Категория «Одежда», занимающая самое высокое положение в иерархии, охватывает все подчиненные категории. Поэтому узлу задаются левый и правый ключ со значениями 1 и 22, причем последнее значение (22) является удвоенной величиной от общего числа представленных узлов (категорий). Следующий иерархический уровень содержит в себе «Мужской» и «Женский» уровни, которые должны быть учтены предыдущим уровнем. Узлу каждого уровня присваиваются значения левого и правого ключей в соответствии с количеством содержащихся в нем подуровней, как показано в данных таблицы.
Можно ожидать, что запросы, использующие вложенное множество, будут быстрее, чем запросы, использующие хранимую процедуру для обхода списка смежности, и поэтому являются более быстрым вариантом для баз данных, в которых отсутствуют встроенные рекурсивные конструкции запросов, таких как MySQL . Однако, можно ожидать, что рекурсивные SQL-запросы будут выполняться сопоставимо для запросов «найти ближайших потомков» и гораздо быстрее для других запросов поиска в глубину, а также являются более быстрым вариантом для баз данных, которые их предоставляют, таких как PostgreSQL , Oracle и Microsoft SQL Server .
Случай использования динамически-бесконечной иерархии дерева баз данных встречается редко. Модель вложенного множества уместна там, где элемент дерева и один или два атрибута являются единственными данными. Модель будет плохим выбором, когда для элементов дерева существуют более сложные реляционные данные. Чтобы учесть произвольную начальную глубину для категории «Транспортные средства» и дочернего элемента «Автомобили» с дочерним элементом «Мерседес», должна быть установлена связь таблицы с помощью внешнего ключа, если только таблица дерева изначально не нормализована. Атрибуты вновь созданного элемента дерева не могут использовать все атрибуты совместно с родительским, дочерним или даже сестринским элементом. Если внешний ключ таблицы установлен для таблицы атрибутов «Растения», то целостность данных дочернего атрибута «Деревья» и его дочернего «Дуба» не предоставляется. Следовательно, в каждом случае для всех атрибутов элемента, вставленного в дерево, должен быть создан внешний ключ таблицы, кроме самых тривиальных вариантов использования.
Если предполагается, что дерево не будет часто меняться, то при первоначальном проектировании системы можно создать правильно нормализованную иерархию таблиц, что приведет к более простым и переносимым SQL-операторам, особенно тем, которые не требуют для изменений в дереве произвольного количества времени выполнения, программно созданных или удаленных таблиц. Для более сложных систем иерархия может быть разработана с помощью реляционных моделей, а не неявной числовой древовидной структуры. Глубина — это просто еще один атрибут, а не основа для всей архитектуры БД. Как сказано в SQL Antipatterns :
Модель вложенного множества это умное решение, может быть, даже слишком умное. Она также не поддерживает ссылочную целостность. Лучше всего используется, когда вам нужно запрашивать дерево чаще, чем его изменять .
Модель не допускает наличие нескольких родительских категорий. Например, «Дуб» может быть дочерним по отношению к «Типу дерева», но также и к «Типу древесины». Для этого необходимо установить дополнительную маркировку или таксономию, что снова приведет к проектировании более сложной структуры, чем простая фиксированная модель.
Вложенные множества очень медленны для вставок, поскольку после вставки требуют обновления значений левого и правого ключа для всех записей в таблице. Это может вызвать большую нагрузку на базу данных, так как многие строки переписываются и индексы перестраиваются. Однако если в таблице можно хранить лес небольших деревьев вместо одного большого дерева, это может значительно снизить расходы, поскольку необходимо обновить только одно маленькое дерево.
Модель вложенных интервалов (англ.) не испытывает такой проблемы, но является более сложной для реализации и не так широко известна. Она по-прежнему страдает от проблемы внешних ключей таблицы. Модель вложенных интервалов хранит положение узлов в виде рациональных чисел, выраженных как коэффициенты (n/d) .
Использование модели вложенного множества имеет некоторые ограничения производительности при выполнении определенных операций обхода дерева. Например, при поиске дочернего узла, заданного родительским узлом, требуется сократить поддерево до определенного уровня, как в следующем примере кода SQL:
SELECT Child.Node, Child.Left, Child.Right
FROM Tree as Parent, Tree as Child
WHERE
Child.Left BETWEEN Parent.Left AND Parent.Right
AND NOT EXISTS ( -- Нет промежуточного узла
SELECT *
FROM Tree as Mid
WHERE Mid.Left BETWEEN Parent.Left AND Parent.Right
AND Child.Left BETWEEN Mid.Left AND Mid.Right
AND Mid.Node NOT IN (Parent.Node, Child.Node)
)
AND Parent.Left = 1 -- Учитывается левый индекс родительского узла
Или, что эквивалентно:
SELECT DISTINCT Child.Node, Child.Left, Child.Right FROM Tree as Child, Tree as Parent WHERE Parent.Left < Child.Left AND Parent.Right > Child.Right -- Объединение дочерних узлов с предками GROUP BY Child.Node, Child.Left, Child.Right HAVING max(Parent.Left) = 1 -- Подмножество тех, у кого данный родительский узел является ближайшим предком
Запрос будет более сложным при поиске потомков в глубину более чем на один уровень. Чтобы преодолеть это ограничение и упростить обход дерева, в модель добавляется дополнительный столбец для хранения глубины узла в дереве.
| Узел | Левый | Правый | Глубина |
|---|---|---|---|
| Одежда | 1 | 22 | 0 |
| Мужская | 2 | 9 | 1 |
| Женская | 10 | 21 | 1 |
| Костюмы | 3 | 8 | 2 |
| Брюки | 4 | 5 | 3 |
| Куртки | 6 | 7 | 3 |
| Платья | 11 | 16 | 2 |
| Юбки | 17 | 18 | 2 |
| Блузки | 19 | 20 | 2 |
| Вечерние платья | 12 | 13 | 3 |
| Сарафаны | 14 | 15 | 3 |
В этой модели поиск дочерних элементов, заданных родительским узлом, может быть выполнен с помощью следующего SQL-запроса:
SELECT Child.Node, Child.Left, Child.Right FROM Tree as Child, Tree as Parent WHERE Child.Depth = Parent.Depth + 1 AND Child.Left > Parent.Left AND Child.Right < Parent.Right AND Parent.Left = 1 -- Учитывается левый индекс родительского узла
Хотя я надеюсь, что информация в данной статье, будет полезна для вас, концепция вложенных множеств в SQL была вокруг в течение более десяти лет, и есть много дополнительной информации, имеющейся в книгах и в интернете. На мой взгляд, наиболее полным источником информации об управлении иерархической информации является книга под названием Деревья Джо Celko и иерархии в SQL для Smarties, написанная очень уважаемым автором в области передовых SQL, Джо Celko. Джо Celko часто приписывают модель вложенных множеств и на сегодняшний день является самым плодовитым автором по этому вопросу. Я нашел книгу Celko, чтобы быть бесценным ресурсом в своих исследованиях и очень рекомендую его. В книге рассматриваются сложные вопросы, которые я не в этой статье, а также предоставляет дополнительные методы для управления иерархическими данными в дополнение к списку смежности и вложенные модели Set.
Анализ данных, представленных в статье про иерархические данные, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое иерархические данные, adjacency list, список смежных вершин, nested set, вложенное множество, materialized path, материализованный путь и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории MySql (Maria DB)
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Базы данных - MySql (Maria DB)
Термины: Базы данных - MySql (Maria DB)