Лекция
Сразу хочу сказать, что здесь никакой воды про гиперкомплексные числа, и только нужная информация. Для того чтобы лучше понимать что такое гиперкомплексные числа, кватернионы , настоятельно рекомендую прочитать все из категории Алгебра.
гиперкомплексные числа — конечномерные алгебры над полем вещественных чисел (то есть числа, над которыми есть пара операций [типа сложения и умножения], также еще «умножение на вещественное число»).
Кватернио́ны (от лат. quaterni, по четыре) — система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел. Обычно обозначаются 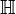 . Предложены Уильямом Гамильтоном в 1843 году.
. Предложены Уильямом Гамильтоном в 1843 году.
Кватернионы удобны для описания изометрий трех- и четырехмерного евклидовых пространств, и поэтому получили широкое распространение в механике. Также их используют в вычислительной математике, например, при создании трехмерной графики.
Анри Пуанкаре писал о кватернионах: «Их появление дало мощный толчок развитию алгебры; исходя от них, наука пошла по пути обобщения понятия числа, придя к концепциям матрицы и линейного оператора, пронизывающим современную математику. Это была революция в арифметике, подобная той, которую сделал Лобачевскийв геометрии» .
Кватернионы были введены Гамильтоном в XVIII веке. Кватернионы являются 4-х мерным расширением множества комплексных чисел, другими словами — это гиперкомплексные числа. То есть кватернион q задается четверкой чисел (x, y, z, w):
w + xi + yj + zk
, где i2 = j2 = k2 = –1.
Его можно также записывать в виде:
[w,v]
, где w называют скаляр, а v = (x, y, z) — вектор.
Кватернионы можно определить как формальную сумму 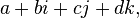 где
где 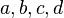 — вещественные числа, а
— вещественные числа, а 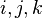 — мнимые единицы со следующим свойством:
— мнимые единицы со следующим свойством: 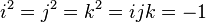 . Таким образом, таблица умножения базисных кватернионов —
. Таким образом, таблица умножения базисных кватернионов — 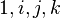 — выглядит так:
— выглядит так:
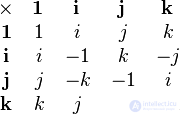
Например, 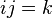 , a
, a  .
.
Кватернион представляет собой пару 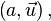 где
где 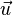 — вектор трехмерного пространства, а
— вектор трехмерного пространства, а 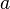 — скаляр, то есть вещественное число.
— скаляр, то есть вещественное число.
Операции сложения определены следующим образом:

Произведение определяется следующим образом:
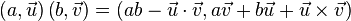
где  обозначает скалярное произведение, а
обозначает скалярное произведение, а 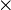 — векторное произведение.
— векторное произведение.
В частности,
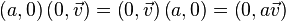
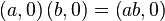
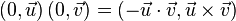
Заметим, что:
Произвольный кватернион  можно представить как пару комплексных чисел в виде
можно представить как пару комплексных чисел в виде
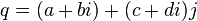
или эквивалентно
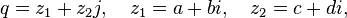
где 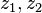 — комплексные числа, поскольку
— комплексные числа, поскольку 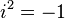 выполняется как для комплексных чисел, так и для кватернионов, а
выполняется как для комплексных чисел, так и для кватернионов, а 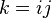 .
.
Кватернионы также можно определить как вещественные матрицы следующего вида с обычными матричными произведением и суммой:
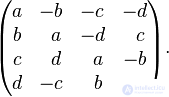
При такой записи:
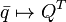 ;
;
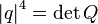 .
.
Альтернативно, кватернионы можно определить как комплексные матрицы следующего вида с обычными матричными произведением и суммой:
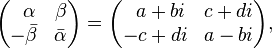
здесь 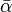 и
и 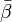 обозначают комплексно-сопряженные числа к
обозначают комплексно-сопряженные числа к 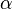 и
и  .
.
Такое представление имеет несколько замечательных свойств:
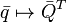 ;
;
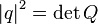 .
.
Для кватерниона
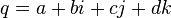
кватернион 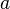 называется скалярной частью
называется скалярной частью 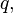 а кватернион
а кватернион 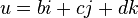 — векторной частью. Если
— векторной частью. Если 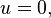 то кватернион называется чисто скалярным, а при
то кватернион называется чисто скалярным, а при 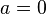 — чисто векторным.
— чисто векторным.
Для кватерниона 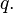 сопряженным называется:
сопряженным называется:
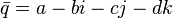
Сопряженное произведение есть произведение сопряженных в обратном порядке:
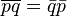
Для кватернионов справедливо равенство
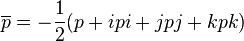
Так же, как и для комплексных чисел,
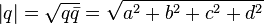
называется модулем 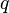 . Если
. Если  то
то 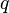 называется единичным кватернионом.
называется единичным кватернионом.
В качестве нормы кватерниона обычно рассматривают его модуль: 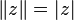 .
.
Таким образом, на множестве кватернионов можно ввести метрику. Кватернионы образуют метрическое пространство, изоморфное 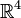 с евклидовой метрикой.
с евклидовой метрикой.
Кватернионы с модулем в качестве нормы образуют банахову алгебру.
Из тождества четырех квадратов вытекает, что 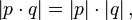 иными словами, кватернионы обладают мультипликативной нормой и образуют ассоциативную алгебру с делением.
иными словами, кватернионы обладают мультипликативной нормой и образуют ассоциативную алгебру с делением.
Кватернион, обратный по умножению к 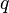 , вычисляется так:
, вычисляется так: 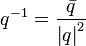 .
.
Четыре базисных кватерниона и четыре противоположных им по знаку образуют по умножению группу кватернионов (порядка 8). Обозначается:
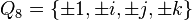 .
.
Множество кватернионов является примером кольца с делением.
Множество кватернионов образует четырехмерную ассоциативную алгебру с делением над полем вещественных (но не комплексных) чисел. Вообще 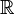 ,
, 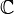 ,
, 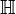 являются единственными конечномерными ассоциативными алгебрами с делением над полем вещественных чисел .
являются единственными конечномерными ассоциативными алгебрами с делением над полем вещественных чисел .
Некоммутативность умножения кватернионов приводит к неожиданным последствиям. Например, количество различных корней полиномиального уравнения над множеством кватернионов может быть больше, чем степень уравнения. В частности, уравнение 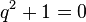 имеет бесконечно много решений — это все единичные чисто векторные кватернионы.
имеет бесконечно много решений — это все единичные чисто векторные кватернионы.

Кватернионы, рассматриваемые как алгебра над 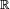 , образуют четырехмерное вещественное векторное пространство. Об этом говорит сайт https://intellect.icu . Любой поворот этого пространства относительно
, образуют четырехмерное вещественное векторное пространство. Об этом говорит сайт https://intellect.icu . Любой поворот этого пространства относительно  может быть записан в виде
может быть записан в виде 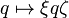 , где
, где 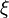 и
и 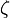 — пара единичных кватернионов, при этом пара
— пара единичных кватернионов, при этом пара 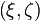 определяется с точностью до знака, то есть один поворот определяют в точности две пары —
определяется с точностью до знака, то есть один поворот определяют в точности две пары — 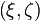 и
и 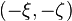 . Из этого следует, что группа Ли
. Из этого следует, что группа Ли 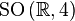 поворотов
поворотов 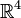 есть факторгруппа
есть факторгруппа 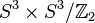 , где
, где 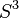 обозначает мультипликативную группу единичных кватернионов.
обозначает мультипликативную группу единичных кватернионов.
Чисто векторные кватернионы образуют трехмерное вещественно векторное пространство. Любой поворот пространства чисто векторных кватернионов относительно  может быть записан в виде
может быть записан в виде 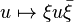 , где
, где 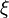 — некоторый единичный кватернион. Соответственно,
— некоторый единичный кватернион. Соответственно, 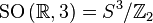 , в частности,
, в частности,  диффеоморфно
диффеоморфно 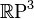 .
.
В качестве нормы кватерниона выберем квадрат его модуля: 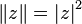 .
.
Целыми по Гурвицу (также engl) принято называть кватернионы 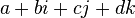 такие, что все
такие, что все 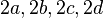 — целые и одинаковой четности.
— целые и одинаковой четности.
Целый кватернион называется
если таким же свойством обладает его норма.
Целый кватернион называется примитивным, если он не делится ни на какое натуральное число, кроме 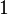 , нацело (иными словами,
, нацело (иными словами, 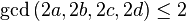 ).
).
Существует 24 целых единичных кватерниона:
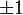 ,
, 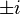 ,
, 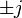 ,
, 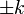 ,
,
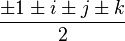 .
.
Они образуют группу по умножению и лежат в вершинах правильного четырехмерного многогранника — кубооктаэдра (не путать с трехмерным многогранником-кубооктаэдром).
Для примитивных кватернионов верен аналог основной теоремы арифметики.
Теорема. Для любого фиксированного порядка множителей в разложении нормы кватерниона 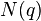 в произведение простых целых положительных чисел
в произведение простых целых положительных чисел 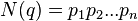 существует разложение кватерниона
существует разложение кватерниона 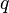 в произведение простых кватернионов
в произведение простых кватернионов 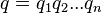 такое, что
такое, что  . Причем данное разложение единственно по модулю домножения на единицы — это значит, что любое другое разложение будет иметь вид
. Причем данное разложение единственно по модулю домножения на единицы — это значит, что любое другое разложение будет иметь вид
 ,
,
где 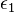 ,
, 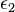 ,
, 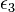 , …
, …  — целые единичные кватернионы.
— целые единичные кватернионы.
Например, примитивный кватернион  имеет норму 60, значит, по модулю домножения на единицы он имеет ровно 12 разложений в произведение простых кватернионов, отвечающих 12 разложениям числа 60 в произведений простых:
имеет норму 60, значит, по модулю домножения на единицы он имеет ровно 12 разложений в произведение простых кватернионов, отвечающих 12 разложениям числа 60 в произведений простых:


Общее число разложений такого кватерниона равно 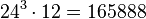
Знак кватерниона вычисляется так:
 .
.
Аргумент кватерниона — это угол поворота четырехмерного вектора, который отсчитывается от вещественной единицы:
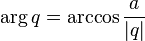 .
.
В дальнейшем используется представление заданного кватерниона 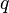 в виде
в виде
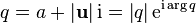
Здесь 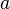 — вещественная часть кватерниона,
— вещественная часть кватерниона, 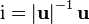 . При этом
. При этом 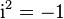 , поэтому проходящая через
, поэтому проходящая через 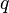 и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид
и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид  для фиксированного единичного вектора
для фиксированного единичного вектора 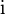 . В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов.
. В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов.
Стандартное определение аналитических функций на ассоциативной нормированной алгебре основано на разложении этих функций в степенные ряды. Рассуждения, доказывающие корректность определения таких функций, полностью аналогичны комплексному случаю и основаны на вычислении радиуса сходимости соответствующих степенных рядов. Учитывая указанное выше «комплексное» представление для заданного кватерниона, соответствующие ряды можно привести к указанной ниже компактной форме. Здесь приведены лишь некоторые наиболее употребительные аналитические функции, аналогично можно вычислить любую аналитическую функцию. Общее правило таково: если 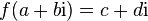 для комплексных чисел, то
для комплексных чисел, то 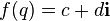 , где кватернион
, где кватернион 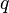 рассматривается в «комплексном» представлении
рассматривается в «комплексном» представлении 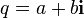 .
.
Степень и логарифм
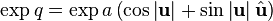
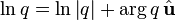
Отметим, что, как обычно в комплексном анализе, логарифм оказывается определен лишь с точностью до 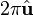 .
.
Тригонометрические функции
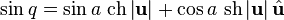
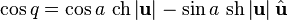
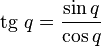
Существуют разные способы определения регулярных функций кватернионного переменного. Самый явный — рассмотрение кватернионно дифференцируемых функций, при этом можно рассматривать праводифференцируемые и леводифференцируемые функции, не совпадающие в силу некоммутативности умножения кватернионов. Очевидно, что их теория полностью аналогична. Определим кватернионно леводифференцируемую функцию  как имеющую предел
как имеющую предел

Оказывается, что все такие функции имеют в некоторой окрестности точки 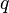 вид
вид
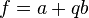
где 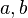 — постоянные кватернионы. Другой способ основан на использовании операторов
— постоянные кватернионы. Другой способ основан на использовании операторов
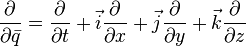
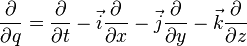
и рассмотрении таких кватернионных функций  , для которых
, для которых
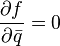
что полностью аналогично использованию операторов 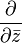 и
и 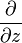 в комплексном случае. При этом получаются аналоги интегральной теоремы Коши, теории вычетов,гармонических функций и рядов Лорана для кватернионных функций .
в комплексном случае. При этом получаются аналоги интегральной теоремы Коши, теории вычетов,гармонических функций и рядов Лорана для кватернионных функций .
Производная Гато функции кватернионного переменного определена согласно формуле
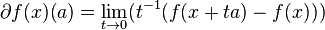
Производная Гато является аддитивным отображением приращения аргумента и может быть представлена в виде

Здесь предполагается суммирование по индексу  . Число слагаемых зависит от выбора функции
. Число слагаемых зависит от выбора функции  . Выражения
. Выражения 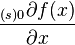 и
и 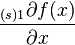 называются компонентами производной.
называются компонентами производной.
Так по-другому называется общепринятое умножение кватернионов ( ).
).
Отличается от общепринятого тем, что вместо первого сомножителя берется сопряженный к нему: 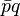 . Оно также некоммутативно.
. Оно также некоммутативно.
Аналогично одноименной операции для векторов:
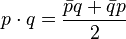 .
.
Эту операцию можно использовать для выделения одного из коэффициентов, например, 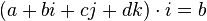 .
.
Определение модуля кватерниона можно видоизменить:
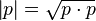 .
.
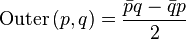 .
.
Используется не очень часто, тем не менее рассматривается в дополнение к скалярному произведению.
Аналогично одноименной операции для векторов. Результатом является тоже вектор:
 .
.

Памятная табличка на мосту Брум Бридж в Дублине: «Здесь на прогулке, 16 октября 1843 года, во вспышке гения, сэр Уильям Роуэн Гамильтон открыл формулу перемножения кватернионов»
Система кватернионов была впервые опубликована Гамильтоном в 1843 году. Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях Гаусса, относящихся к 1819—1820 годам.
Бурное и чрезвычайно плодотворное развитие комплексного анализа в XIX веке стимулировало у математиков интерес к следующей задаче: найти новый вид чисел, аналогичный по свойствам комплексным, но содержащий не одну, а две мнимые единицы. Предполагалось, что такая модель будет полезна при решении пространственных задач математической физики. Однако работа в этом направлении оказалась безуспешной.
Новый вид чисел был обнаружен ирландским математиком Уильямом Гамильтоном в 1843 году, и он содержал не две, как ожидалось, а три мнимые единицы. Гамильтон назвал эти числа кватернионами. Позднее Фробениус строго доказал (1877)теорему, согласно которой расширить комплексное поле до поля или тела с двумя мнимыми единицами невозможно.
Несмотря на необычные свойства новых чисел (их некоммутативность), эта модель довольно быстро принесла практическую пользу. Максвелл использовал компактную кватернионную запись для формулировки своих уравнений электромагнитного поля.[10]Позднее на основе алгебры кватернионов был создан трехмерный векторный анализ (Гиббс, Хевисайд).
В XX веке были сделаны несколько попыток использовать кватернионные модели в квантовой механике[11] и теории относительности[12]. Реальное применение кватернионы нашли в современной компьютерной графике и программировании игр[13], а также в вычислительной механике[14][15], в инерциальной навигации и теории управления[16][17]. С 2003 года издается журнал «Гиперкомплексные числа в геометрии и физике»[18].
Во многих областях применения были найдены более общие и практичные средства, чем кватернионы. Например, в наши дни для исследования движений в пространстве чаще всего применяется матричное исчисление[19]. Однако там, где важно задавать трехмерный поворот при помощи минимального числа скалярных параметров, использование параметров Родрига — Гамильтона (то есть четырех компонент кватерниона поворота) весьма часто оказывается предпочтительным: такое описание никогда не вырождается, а при описании поворотов тремя параметрами (например, углами Эйлера) всегда существуют критические значения этих параметров, когда описание вырождается[14][15].
Как алгебра над 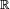 , кватернионы образуют вещественное векторное пространство
, кватернионы образуют вещественное векторное пространство  , снабженное тензором третьего ранга
, снабженное тензором третьего ранга 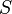 типа (1,2), иногда называемогоструктурным тензором. Как всякий тензор такого типа,
типа (1,2), иногда называемогоструктурным тензором. Как всякий тензор такого типа, 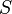 отображает каждую 1-форму
отображает каждую 1-форму 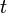 на
на  и пару векторов
и пару векторов  из
из  в вещественное число
в вещественное число 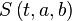 . Для любой фиксированной 1-формы
. Для любой фиксированной 1-формы 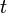
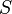 превращается в ковариантный тензор второго ранга, который, в случае его симметрии, становится скалярным произведением на
превращается в ковариантный тензор второго ранга, который, в случае его симметрии, становится скалярным произведением на  . Поскольку каждое вещественное векторное пространство является также вещественным линейным многообразием, такое скалярное произведение порождает тензорное поле, которое, при условии его невырожденности, становится (псевдо- или собственно-)евклидовой метрикой на
. Поскольку каждое вещественное векторное пространство является также вещественным линейным многообразием, такое скалярное произведение порождает тензорное поле, которое, при условии его невырожденности, становится (псевдо- или собственно-)евклидовой метрикой на  . В случае кватернионов это скалярное произведение индефинитно, его сигнатура не зависит от 1-формы
. В случае кватернионов это скалярное произведение индефинитно, его сигнатура не зависит от 1-формы 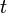 , а соответствующая псевдоевклидова метрика есть метрика Минковского[20]. Эта метрика автоматически продолжается на группу Ли ненулевых кватернионов вдоль ее левоинвариантных векторных полей, образуя так называемую закрытую ФЛРУ (Фридман — Леметр — Робертсон — Уолкер) метрику[21] — важное решение уравнений Эйнштейна. Эти результаты проясняют некоторые аспекты проблемы совместимости квантовой механики и общей теории относительности в рамках теории квантовой гравитации[22].
, а соответствующая псевдоевклидова метрика есть метрика Минковского[20]. Эта метрика автоматически продолжается на группу Ли ненулевых кватернионов вдоль ее левоинвариантных векторных полей, образуя так называемую закрытую ФЛРУ (Фридман — Леметр — Робертсон — Уолкер) метрику[21] — важное решение уравнений Эйнштейна. Эти результаты проясняют некоторые аспекты проблемы совместимости квантовой механики и общей теории относительности в рамках теории квантовой гравитации[22].
Существует несколько путей представления вращения объектов. Многие программисты используют для этого матрицы вращения или углы Эйлера. Каждое из этих решений работает замечательно, до тех пор, пока вы не пытаетесь осуществить гладкую интерполяцию между двумя разными положениями объекта. Например, представьте себе объект, который просто свободно вращается в пространстве. Если хранить вращение, как матрицу или в виде углов Эйлера, то гладкая интерполяция окажется довольно дорогостоящей по вычислениям и будет не столь гладкой, как при интерполяции кватернионами. Хотя и можно попытаться наиболее близко расставить временные ключи на стадии создания анимации, однако это влечет за собой хранение большего количества данных для данного вращения и не совсем тривиально ясно, какой выбирать шаг. Понятно, что и в этом случае без интерполяции не обойтись, никогда не известно какой FPS будет у игрока.
Многие игры от третьего лица используют кватернионы для анимации движения камеры. Все игры от третьего лица располагают камеру на некотором расстоянии от персонажа. Так как камера имеет другое движение, отличающееся от движения персонажа, например, при повороте персонажа - камера движется по дуге, то иногда бывает, что это движение выглядит не натурально, скачками. Это одна из проблем, которую можно решить при помощи кватернионов. Кватернионы также удобно использовать в летных симуляторах, таких как ИЛ-2 Штурмовик. Вместо манипулирования тремя углами (roll, pitch и yaw), представляя вращение вокруг осей x, y и z соответственно, намного проще использовать один кватернион. Да и вообще много игр и приложений трехмерной графики сохраняют ориентацию объектов в кватернионах. Например, легче добавить угловую скорость к кватерниону, чем к матрице.
Рассмотрим два кватерниона: q[w,v] и q'[w',v']. Для них справедливо следующее:
q+q' = [w+w',v+v']
qq' = [ww' – v·v', vxv' + wv' + w'v]
, где x - векторное произведение, а · — скалярное.
norm(q) = sqrt(w2+x2+y2+z2) (размер)
q*=[w, –v] (сопряжение)
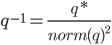
norm(q)=1 => q–1=q*
Кватернионы расширяют концепцию вращения в трехмерном пространстве до вращения в четырехмерном. Вращение можно задать единичным кватернионом (norm(q) = 1). Чтобы кватернион привести к единичному виду, или другими словами нормализовать, необходимо вычислить его размер norm(q) и все четыре члена кватерниона разделить на величину полученного размера.
Пространство кватернионов представляет собой 4-х мерное пространство. Множество всех единичных векторов — есть 4-х мерная сфера с радиусом 1. Кватернионы можно рассматривать, как добавление дополнительного угла поворота к сферическим координатам, (сферические координаты - долгота, широта, угол поворота).
Если вращение задано некоторым кватернионом q, то вектор v после вращения будет иметь вид v':
V'=q V q–1
, где V = [o,v], V'=[0,v']
Рассмотрим вращение на угол Q вокруг оси, заданной направляющим вектором v. Это вращение можно задать кватернионом:
q=[cos(Q/2),sin(Q/2)v]
При необходимости нужно не забыть нормализовать полученный кватернион.
struct Quaternion{
float x,y,z; // Вектор
float w; // Скаляр
};
//Преобразование сферических кординат в кватернион
void SphericalToQuaternion(Quaternion * q, float latitude, float longitude,
float angle)
{
float sin_a = sin( angle / 2 );
float cos_a = cos( angle / 2 );
float sin_lat = sin( latitude );
float cos_lat = cos( latitude );
float sin_long = sin( longitude );
float cos_long = cos( longitude );
q->x = sin_a * cos_lat * sin_long;
q->y = sin_a * sin_lat;
q->z = sin_a * sin_lat * cos_long;
q->w = cos_a;
}
Вращение задается yaw, pitch и roll. Тогда кватернион вычисляется следующим образом:
qroll = [cos (y/2), (sin(y/2), 0, 0)]
qpitch = [cos (q/2), (0, sin(q/2), 0)]
qyaw = [cos (f/2), (0, 0, sin(f/2))]
q = qyaw qpitch qroll
Для задания вращения достаточно матрицы размером 3x3. Однако, поскольку многие 3D API используют для трансформации матрицы размером 4x4, мы тоже будем рассматривать такую размерность матрицы. При этом, чтобы дополнительные данные не влияли на смысл матрицы, дополнительные строка и столбец выставляются в ноль, за исключением их пересечения, которое выставляется в 1. Ниже приведен код преобразования матрицы поворота в кватернион. Ясно, что эта матрица не должна нести в себе другую информацию кроме вращения, например — масштабирование.
// Преобразование матрицы в кватернион
void MatrixToQuaternion(Quaternion * quat, float m )
{
float tr, s, q ;
int i, j, k;
int nxt = {1, 2, 0};
tr = m + m + m ;
if (tr > 0.0)
{
s = sqrt (tr + 1.0);
quat->w = s / 2.0;
s = 0.5 / s;
quat->x = (m - m ) * s;
quat->y = (m - m ) * s;
quat->z = (m - m ) * s;
}
else
{
i = 0;
if (m > m ) i = 1;
if (m > m[i][i]) i = 2;
j = nxt[i];
k = nxt[j];
s = sqrt ((m[i][i] - (m[j][j] + m[k][k])) + 1.0);
q[i] = s * 0.5;
if (s != 0.0) s = 0.5 / s;
q = (m[j][k] - m[k][j]) * s;
q[j] = (m[i][j] + m[j][i]) * s;
q[k] = (m[i][k] + m[k][i]) * s;
quat->x = q ;
quat->y = q ;
quat->z = q ;
quat->w = q ;
}
}
Преобразование единичного кватерниона в матрицу поворота можно записать в виде:
TRot = [ 1-2y2-2z2 2xy-2wz 2xz+2wy
2xy+2wz 1-2x2-2z2 2yz-2wx
2xz-2wy 2yz+2wx 1-2x2-2y2 ]
// Преобразование кватерниона в матрицу
void QuaternionToMatrix(float m , const Quaternion * quat)
{
float wx, wy, wz, xx, yy, yz, xy, xz, zz, x2, y2, z2;
x2 = quat->x + quat->x;
y2 = quat->y + quat->y;
z2 = quat->z + quat->z;
xx = quat->x * x2; xy = quat->x * y2; xz = quat->x * z2;
yy = quat->y * y2; yz = quat->y * z2; zz = quat->z * z2;
wx = quat->w * x2; wy = quat->w * y2; wz = quat->w * z2;
m =1.0f-(yy+zz); m =xy-wz; m =xz+wy;
m =xy+wz; m =1.0f-(xx+zz); m =yz-wx;
m =xz-wy; m =yz+wx; m =1.0f-(xx+yy);
m = m = m = 0;
m = m = m = 0;
m = 1;
}
При работе с иерархией объектов и инверсной кинематикой возникает композитное задание вращения. В этом случае использование кватернионов предпочтительнее, чем матриц. То есть, если вращение задано двумя матрицами R1 и R2, то чтобы вычислить матрицу поворота нужно перемножить эти матрицы: R = R1 x R2. Аналогично, если вращение задано двумя кватернионами q1 и q2, то результирующий кватернион поворота будет q = q1 x q2. Ясно, что вычисление произведения кватернионов происходит быстрее, чем матриц. Причем произведение кватернионов можно оптимизировать:
void MulQuaternions(Quaternion *res,
const Quaternion *q1, const Quaternion *q2)
{
float A, B, C, D, E, F, G, H;
A = (q1->w + q1->x) * (q2->w + q2->x);
B = (q1->z - q1->y) * (q2->y - q2->z);
C = (q1->x - q1->w) * (q2->y + q2->z);
D = (q1->y + q1->z) * (q2->x - q2->w);
E = (q1->x + q1->z) * (q2->x + q2->y);
F = (q1->x - q1->z) * (q2->x - q2->y);
G = (q1->w + q1->y) * (q2->w - q2->z);
H = (q1->w - q1->y) * (q2->w + q2->z);
res->w = B + (-E - F + G + H) * 0.5;
res->x = A - ( E + F + G + H) * 0.5;
res->y =-C + ( E - F + G - H) * 0.5;
res->z =-D + ( E - F - G + H) * 0.5;
}
Одним из наиболее полезных свойств кватернионов является достижение гладкой анимации при интерполяции. Рассмотрим интерполяцию между двумя кватернионами, которые задают вращение. При этом интерполяция происходит вдоль кратчайшей дуги. Этого можно достичь при помощи сферической линейной интерполяции (SLERP - Spherical Linear intERPolation):
SLERP(t) = (p sin((1–t)a) – q sin(ta)) / sin(a)
где q и p - кватернионы.
t - изменяется от 0 до 1,
a - угол между q и p, cos(a) = (q,p)/(|q|*|p|) = (q,p).
При очень маленьких a, чтобы избежать деления на ноль, пользуйтесь обычной линейной интерполяцией. Реализация:
void Slerp(Quaternion * res
Quaternion * q, Quaternion * p, float t)
{
float p1 ;
double omega, cosom, sinom, scale0, scale1;
// косинус угла
cosom = q->x*p->x + q->y*p->y + q->z*p->z + q->w*p->w;
if ( cosom <0.0 )
{
cosom = -cosom;
p1 = - p->x; p1 = - p->y;
p1 = - p->z; p1 = - p->w;
}
else
{
p1 = p->x; p1 = p->y;
p1 = p->z; p1 = p->w;
}
if ( (1.0 - cosom) > DELTA )
{
// стандартный случай (slerp)
omega = acos(cosom);
sinom = sin(omega);
scale0 = sin((1.0 - t) * omega) / sinom;
scale1 = sin(t * omega) / sinom;
}
else
{
// если маленький угол - линейная интерполяция
scale0 = 1.0 - t;
scale1 = t;
}
res->x = scale0 * q->x + scale1 * p1 ;
res->y = scale0 * q->y + scale1 * p1 ;
res->z = scale0 * q->z + scale1 * p1 ;
res->w = scale0 * q->w + scale1 * p1 ;
}
Вместе с DirectX SDK поставляется утилитная библиотека Direct3DX utility library. В ней немного места уделено и кватернионам. Кватернион задается структурой:
typedef struct D3DXQUATERNION {
FLOAT x,y,z,w;
} D3DXQUATERNION;
Есть набор функций для работы со стандартными возможностями кватернионов:
Перемножение двух кватернионов:
D3DXQuaternionMultiply()
Получить размер:
D3DXQuaternionLength()
Нормализация:
D3DXQuaternionNormalize()
Преобразование улов Эйлера в кватернион:
D3DXQuaternionRotationYawPitchRoll()
Преобразование матрицы вращения в кватернион и обратно:
D3DXQuaternionRotationMatrix()
D3DXMatrixRotationQuaternion()
Сферическая линейная интерполяция:
D3DXQuaternionSlerp()
И т.д. Полное описание всех функций смотрите в DirectX SDK.
В Max SDK кватернионы описываются классом С++:
class Quat{...};
Класс наполнен необходимыми методами и операторами. Конструкции языка С++ позволяют перегружать операторы, например, для кватернионов можно записать сумму в более читаемом виде:
q = q1+q2;
Кроме методов класса Quat, в классе для матриц Matrix3 есть метод преобразования из кватерниона:
void SetRotate(const Quat& q);
Кватернион, задающий вращение, можно получить для любого объекта сцены. Трансформация хранится в объектах класса INode. Сначала, нужно получить контроллер вращения из контроллера трансформации, затем воспользоваться методом GetValue() для этого контроллера:
void GetQuat(Quat * pQuat, const pNode * pNode)
{
Control * pTransf = pNode->GetTMController();
if(pTransf)
{
Control * pCtrl = pTransf->GetRotationController();
if(pCtrl)
pCtrl->GetValue(0, pQuat, NEVER, CTRL_ABSOLUTE);
}
}
Во время экспорта будьте внимательны с координатными системами. Ваша координатная система может не совпадать с координатной системой выбранной в 3D Studio MAX. Например, ось z здесь направлена вверх, а многие другие API, включая DirectX и OpenGL, направляют вверх ось y. По этой причине в полученных кватернионах параметр y может не соответствовать вашему y. Например, при экспорте в координатную систему DirectX можно пользоваться следующим преобразованием, обратите внимание на знаки и на компоненты y и z:
dx_quat.x = -max_quat.x; dx_quat.y = -max_quat.z; dx_quat.z = -max_quat.y; dx_quat.w = max_quat.w;
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про гиперкомплексные числа Надеюсь, что теперь ты понял что такое гиперкомплексные числа, кватернионы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгебра
Комментарии
Оставить комментарий
Алгебра
Термины: Алгебра