Лекция
Сразу хочу сказать, что здесь никакой воды про функция, и только нужная информация. Для того чтобы лучше понимать что такое функция, математическая функция , настоятельно рекомендую прочитать все из категории введение в математику. основы.
функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементамимножеств. Другими словами, функция — это правило, по которому каждому элементу одного множества (называемогообластью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной 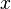 однозначно определяет значение выражения
однозначно определяет значение выражения 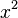 , а значение месяцаоднозначно определяет значение следующего за ним месяца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдает определенные выходные данные.
, а значение месяцаоднозначно определяет значение следующего за ним месяца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдает определенные выходные данные.
Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.
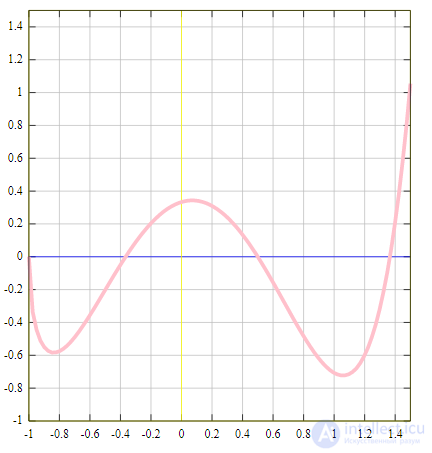
График функции
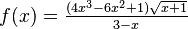 .
.
Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем (1692 год). В свою очередь, Иоганн Бернулли в письме к тому же Лейбницу употребил этот термин в смысле, более близком к современному .
Первоначально, понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, данное Эйлером (1751 год), затем — у Лакруа (1806 год) — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским (1834 год) и Дирихле (1837 год) .
К концу XIX века понятие функции переросло рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввел логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.
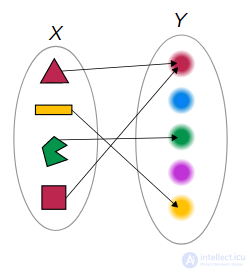
Функция, сопоставляющая каждой из четырех фигур ее цвет.
Наиболее строгим определением функции является теоретико-множественное определение (на основе понятия бинарного отношения). Часто вместо определения функции дается ее интуитивное описание; то есть понятие функции переводится на обычный язык, используя слова «закон», «правило» или «соответствие».
Функция  (отображение, операция, оператор) — это закон или правило, согласно которому каждому элементу
(отображение, операция, оператор) — это закон или правило, согласно которому каждому элементу 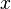 из множества
из множества 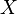 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 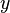 из множества
из множества 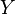 .
.
При этом говорят, что функция  задана на множестве
задана на множестве 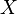 , или что
, или что  отображает
отображает 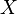 в
в 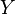 .
.
Если элементу 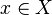 сопоставлен элемент
сопоставлен элемент  , то говорят, что элемент
, то говорят, что элемент 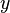 находится в функциональной зависимости
находится в функциональной зависимости  от элемента
от элемента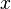 . При этом переменная
. При этом переменная 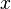 называется аргументом функции
называется аргументом функции  или независимой переменной, множество
или независимой переменной, множество 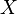 называется областью задания или областью определения функции, а элемент
называется областью задания или областью определения функции, а элемент 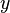 , соответствующий конкретному элементу
, соответствующий конкретному элементу 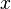 — частным значением функции
— частным значением функции  в точке
в точке 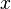 . Множество
. Множество 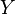 всех возможных частных значений функции
всех возможных частных значений функции  называется ее областью значений или областью изменения.
называется ее областью значений или областью изменения.
Функция 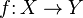 есть множество упорядоченных пар
есть множество упорядоченных пар 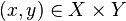 ), которое удовлетворяет следующему условию: для любого
), которое удовлетворяет следующему условию: для любого 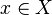 существует единственный элемент
существует единственный элемент  такой, что
такой, что 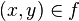 .
.
Таким образом, функция — это упорядоченная тройка (или кортеж) объектов 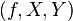 , где
, где
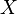 называется о́бластью определе́ния;
называется о́бластью определе́ния;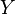 называется о́бластью значе́ний;
называется о́бластью значе́ний; или, что то же самое, график функции.
или, что то же самое, график функции.Если задана функция  , которая определена на множестве
, которая определена на множестве 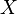 и принимает значения в множестве
и принимает значения в множестве 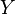 , то есть, функция
, то есть, функция  отображает множество
отображает множество 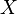 в
в 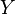 , то
, то
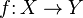 или
или 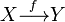 .
. (множество
(множество  ) обозначается
) обозначается 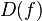 , или
, или  ;
; (множество
(множество 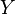 ) обозначается
) обозначается  (
(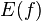 ), или
), или 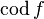 (
(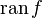 ).
).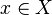 и элементом
и элементом  наиболее часто обозначается как
наиболее часто обозначается как
 ,
,
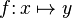 или
или
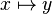 ;
;
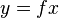 ,
, 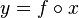 или
или 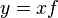 ,
,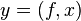 или
или 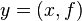 ;
;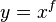 , которое можно встретить в общей алгебре.
, которое можно встретить в общей алгебре. в лямбда-исчислении Черча.
в лямбда-исчислении Черча.Понятие функции одной переменной легко обобщается на случай двух и большего числа аргументов.
В случае функции двух переменных будем рассматривать множество упорядоченных пар (x,y), где числовые значения x и y принадлежат множествам x∈X, y∈Y. Если задан закон, согласно которому каждой паре (x,y) соответствует единственное числовое значение z, то говорят, что задана функция двух переменных
. Обычно такая функция обозначается в виде z=z(x,y), z=f(x,y), z=F(x,y) и т.д.
В практике встречаются, однако, функции, зависящие от трех или большего числа переменных. Например, объем V прямоугольного параллелепипеда зависит от трех величин — длины а и ширины b его основания и высоты h параллелепипеда: 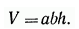
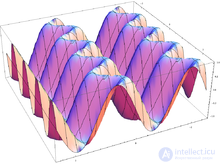
График функции двух переменных: 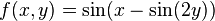
Дадим определение функции трех переменных.
Определение. Переменная и называется функцией трех переменных х, у и z, если:
1) задано множество Q троек численных значений х, у и z;
2) задан закон, по которому каждой тройке чисел (х, у,z) из этого множества соответствует единственное значение u.
Переменные х, у и z называются при этом аргументами функции и или независимыми переменными.
Множество  которое образуют все тройки (х, у,z) численных значений аргументов х, у и z, называется областью определения или областью задания функции трех переменных.
которое образуют все тройки (х, у,z) численных значений аргументов х, у и z, называется областью определения или областью задания функции трех переменных.
Обозначаются функции трех переменных так же, как и функции одной или двух переменных: 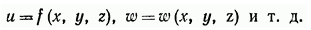
Функцию трех переменных 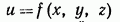 можно рассматривать как функцию точки
можно рассматривать как функцию точки 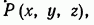 , имеющей координаты х, у,z в пространственной системе координат
, имеющей координаты х, у,z в пространственной системе координат 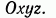 .
.
Пользуясь геометрической терминологией, аналогичной той, которую мы приняли для функции двух переменных, скажем, что область определения функции 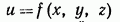 есть некоторое множество точек в пространстве.
есть некоторое множество точек в пространстве.
Способы задания функций трех переменных 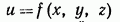 могут быть самыми различными, но важнейшим в нашем курсе будет аналитический способ задания, когда функция задается с помощью аналитического выражения (формулы). При этом часто область определения функции не указывается. В последнем случае областью определения (областью задания) функции принято считать множество всех тех точек
могут быть самыми различными, но важнейшим в нашем курсе будет аналитический способ задания, когда функция задается с помощью аналитического выражения (формулы). При этом часто область определения функции не указывается. В последнем случае областью определения (областью задания) функции принято считать множество всех тех точек 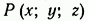 пространства, для которых это выражение имеет смысл и дает действительное значение функции u.
пространства, для которых это выражение имеет смысл и дает действительное значение функции u.
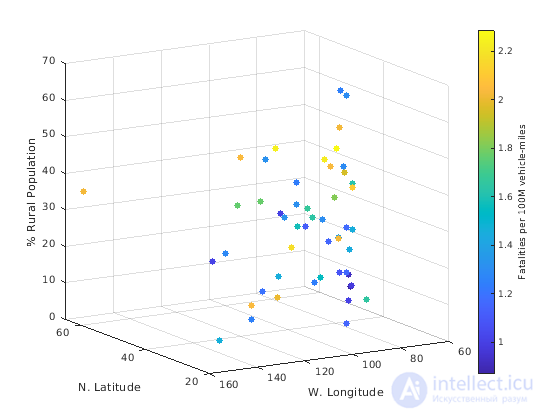
Визуализация функции трех переменных
Для многих видов четырехмерных данных можно использовать цвет, чтобы представлять четвертую размерность. Это работает хорошо, если у вас есть функция трех переменных.
Например, представляйте магистральные смертельные случаи в Соединенных Штатах как функция долготы, широты, и если местоположение является сельским или городским. X, y, и z значения в графике представляют эти три переменные. Цвет представляет количество магистральных смертельных случаев.
Аналогичным образом определяется функция n переменных.
Определение функции легко обобщить на случай функции многих аргументов.
Если множество 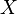 представляет собой декартово произведение множеств
представляет собой декартово произведение множеств 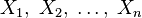 , тогда отображение
, тогда отображение 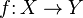 оказывается
оказывается 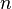 -местным отображением, при этом элементы упорядоченного набора
-местным отображением, при этом элементы упорядоченного набора 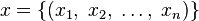 называются аргументами (данной
называются аргументами (данной 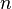 -местной функции), каждый из которых пробегает свое множество:
-местной функции), каждый из которых пробегает свое множество:
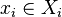 где
где 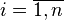 .
.
В этом случае 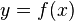 означает, что
означает, что 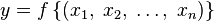 .
.
Функция как математический объект представляет собой бинарное отношение, удовлетворяющее определенным условиям. Функцию можно задать непосредственно как множество упорядоченных пар, например: 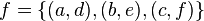 есть функция
есть функция 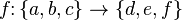 . Однако, этот способ совершенно непригоден для функций на бесконечных множествах (каковыми являются привычные вещественные функции: степенная, линейная, показательная, логарифмическая и т. п.).
. Однако, этот способ совершенно непригоден для функций на бесконечных множествах (каковыми являются привычные вещественные функции: степенная, линейная, показательная, логарифмическая и т. п.).
Для задания функции пользуются выражением: 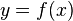 . При этом,
. При этом, 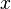 есть переменная, пробегающая область определения функции, а
есть переменная, пробегающая область определения функции, а 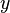 — область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы. Это могут быть числа, векторы, матрицы, яблоки, цвета радуги. Поясним на примере:
— область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы. Это могут быть числа, векторы, матрицы, яблоки, цвета радуги. Поясним на примере:
Пусть имеется множество  яблоко, самолет, груша, стул
яблоко, самолет, груша, стул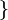 и множество
и множество 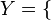 человек, паровоз, квадрат
человек, паровоз, квадрат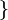 . Зададим функцию f следующим образом:
. Зададим функцию f следующим образом: 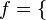 (яблоко, человек), (самолет, паровоз), (груша, квадрат), (стул, человек)
(яблоко, человек), (самолет, паровоз), (груша, квадрат), (стул, человек)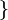 . Если ввести переменную x, пробегающую множество
. Если ввести переменную x, пробегающую множество 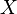 и переменную y, пробегающую множество
и переменную y, пробегающую множество 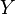 , указанную функцию можно задать аналитически, как:
, указанную функцию можно задать аналитически, как: 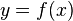 .
.
Аналогично можно задавать числовые функции. Например: 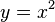 , где х пробегает множество вещественных чисел, задает некоторую функцию f. Важно понимать, что само выражение
, где х пробегает множество вещественных чисел, задает некоторую функцию f. Важно понимать, что само выражение 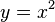 не является функцией. Функция, как объект, представляет собой множество (упорядоченных пар). А данное выражение, как объект, есть равенство двух переменных. Оно задает функцию, но не является ею.
не является функцией. Функция, как объект, представляет собой множество (упорядоченных пар). А данное выражение, как объект, есть равенство двух переменных. Оно задает функцию, но не является ею.
Однако, во многих разделах математики, можно обозначать через f(x) как саму функцию, так и аналитическое выражение, ее задающее. Это синтаксическое соглашение является крайне удобным и оправданным.
Числовые функции можно также задавать с помощью графика. Пусть 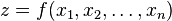 — вещественная функция n переменных.
— вещественная функция n переменных.
Рассмотрим некоторое (n+1)-мерное линейное пространство над полем вещественных чисел (так как функция вещественная). Выберем в этом пространстве любой базис (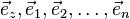 ). Об этом говорит сайт https://intellect.icu . Каждой точке функции сопоставим вектор:
). Об этом говорит сайт https://intellect.icu . Каждой точке функции сопоставим вектор: 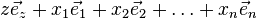 . Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
. Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
Если в качестве линейного пространства взять евклидово пространство свободных геометрических векторов (направленных отрезков), а число аргументов функции f не превосходит 2, указанное множество точек можно изобразить наглядно в виде чертежа (графика). Если сверх того исходный базис взять ортонормированным, получим «школьное» определение графика функции.
Для функций 3 аргументов и более такое представление не применимо ввиду отсутствия у человека геометрической интуиции многомерных пространств.
Однако, и для таких функций можно придумать наглядное полугеометрическое представление (например каждому значению четвертой координаты точки сопоставить некоторый цвет на графике).
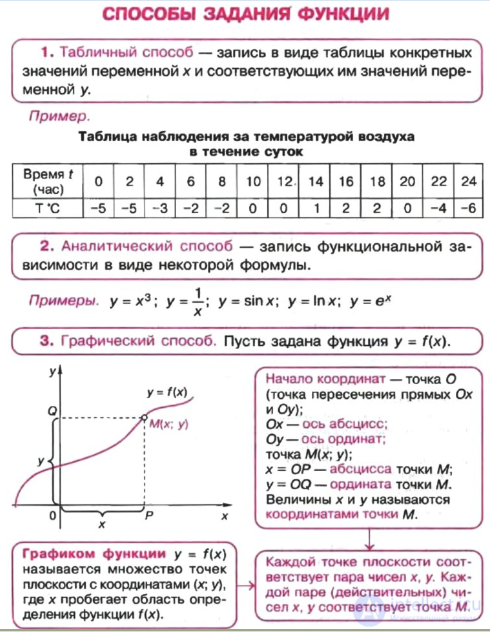
Например, если измерять температуру воздуха каждый час в течении суток, то каждому часу (t) будет соответствовать определенная температура (T). Такое соответствие можно записать в виде таблицы:
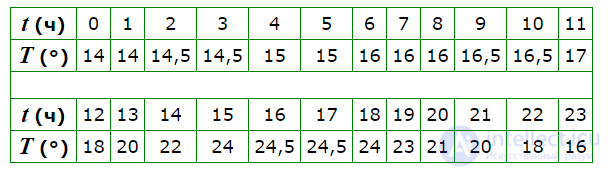
Следовательно, T функция от t – T(t), определенная с помощью множества целых чисел от 0 до 24 и заданная таблицей. Соответствие между величинами двух переменных задается в данном случае не формулой, а таблицей.
Пусть дано отображение 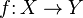 и
и 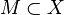 .
.
Отображение 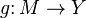 , которое принимает на
, которое принимает на 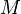 те же значения, что и функция
те же значения, что и функция  , называется суже́нием (или, иначе ограничением) функции
, называется суже́нием (или, иначе ограничением) функции  на множество
на множество 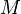 .
.
Сужение функции  на множество
на множество 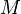 обозначается как
обозначается как 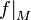 .
.
Если функция 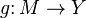 такова, что она является сужением для некоторой функции
такова, что она является сужением для некоторой функции 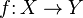 , то функция
, то функция  , в свою очередь, называется продолжением функции
, в свою очередь, называется продолжением функции 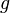 на множество
на множество 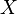 .
.
Элемент 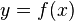 , который сопоставлен элементу
, который сопоставлен элементу 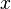 , называется образом элемента (точки)
, называется образом элемента (точки) 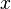 (при отображении
(при отображении  ).
).
Если взять целое подмножество 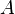 области определения функции
области определения функции  , то можно рассмотреть совокупность образов всех элементов множества
, то можно рассмотреть совокупность образов всех элементов множества 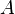 , а именно подмножество области значений (функции
, а именно подмножество области значений (функции  ) вида
) вида
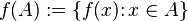 ,
,
которое, называется образом множества 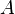 (при отображении
(при отображении  ). Это множество иногда обозначается как
). Это множество иногда обозначается как  или
или 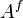 .
.
Наоборот, взяв некоторое подмножество 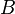 области значений функции
области значений функции  , можно рассмотреть совокупность тех элементов области определения (функции
, можно рассмотреть совокупность тех элементов области определения (функции  ), чьи образы попадают в множество
), чьи образы попадают в множество 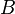 , а именно — множество вида
, а именно — множество вида
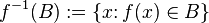 ,
,
которое называется (полным) прообразом множества 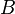 (при отображении
(при отображении  ).
).
В том частном случае, когда множество 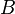 состоит из одного элемента, скажем,
состоит из одного элемента, скажем, 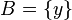 , множество
, множество  имеет более простое обозначение
имеет более простое обозначение 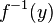 .
.
Отображения, у которых совпадают область определения и область значений, называются отображениями заданного множества в себя или преобразованиями.
В частности, преобразование 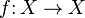 , которое сопоставляет каждой точке
, которое сопоставляет каждой точке 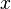 множества
множества 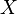 ее саму или, что тоже самое,
ее саму или, что тоже самое,
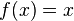 для каждого
для каждого 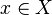 ,
,
называется тождественным.
Это отображение имеет специальное обозначение: 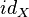 или, проще,
или, проще, 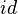 (если из контекста понятно, какое множество имеется в виду). Такое обозначение обязано своим происхождением англ. слову identity («идентичность, тождественность»).
(если из контекста понятно, какое множество имеется в виду). Такое обозначение обязано своим происхождением англ. слову identity («идентичность, тождественность»).
Другое обозначение тождественного преобразования — 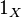 . Такое отображение является унарной операцией, заданной на множестве
. Такое отображение является унарной операцией, заданной на множестве 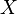 . Поэтому, нередко, тождественное преобразование называют единичным.
. Поэтому, нередко, тождественное преобразование называют единичным.
Пусть 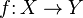 и
и 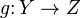 — два заданных отображения таких, что область значений первого отображения является подмножеством области определения второго отображения. Тогда для всякого
— два заданных отображения таких, что область значений первого отображения является подмножеством области определения второго отображения. Тогда для всякого 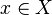 однозначно определяется элемент
однозначно определяется элемент  такой, что
такой, что 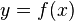 , но для этого самого
, но для этого самого 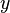 однозначно определяется элемент
однозначно определяется элемент  такой, что
такой, что 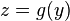 . То есть, для всякого
. То есть, для всякого 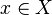 однозначно определяется элемент
однозначно определяется элемент  такой, что
такой, что 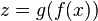 . Другими словами, определено отображение
. Другими словами, определено отображение 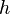 такое, что
такое, что
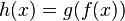 для всякого
для всякого 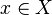 .
.
Это отображение называется композицией отображений  и
и 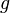 и обозначается
и обозначается
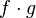 или
или 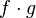 ,
, (именно в таком порядке!), что является наиболее употребительным.
(именно в таком порядке!), что является наиболее употребительным.Если отображение 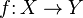 является взаимно однозначным или биективным (см. ниже), то определено отображение
является взаимно однозначным или биективным (см. ниже), то определено отображение  , у которого
, у которого
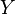 ) совпадает с областью значений отображения
) совпадает с областью значений отображения  ;
;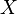 ) совпадает с областью определения отображения
) совпадает с областью определения отображения  ;
;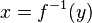 тогда и только тогда, когда
тогда и только тогда, когда 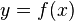 .
.Такое отображение называется обратным по отношению к отображению  .
.
Отображение, у которого определено обратное, называется обратимым.
В терминах композиции функции, свойство обратимости заключается в одновременном выполнении двух условий: 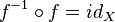 и
и 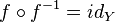 .
.
Пусть задана функция 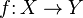 , где
, где 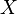 и
и 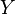 — данные множества, причем
— данные множества, причем 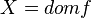 . Каждая такая функция может обладать некоторыми свойствами, описание которых приведено ниже.
. Каждая такая функция может обладать некоторыми свойствами, описание которых приведено ниже.
Взятие образа
Положим, 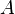 и
и 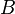 — подмножества области определения. Взятие образа (или, что то же самое, применение оператора
— подмножества области определения. Взятие образа (или, что то же самое, применение оператора  ) обладает следующими свойствами:
) обладает следующими свойствами:
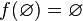 ;
;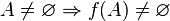 ;
;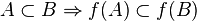 .
.Далее
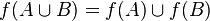 ;
; .
.Последние два свойства, вообще говоря, допускают обобщение на любое количество множеств, большее двух (как оно здесь сформулировано).
Взятие прообраза
Положим, 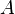 и
и 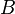 — подмножества множества
— подмножества множества 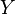 .
.
По аналогии с взятием образа, взятие прообраза (переход к прообразу) обладает также следующими двумя очевидными свойствами:
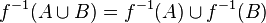 ;
;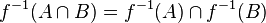 .
.Данные свойства, также, допускают обобщение на любое количество множеств, большее двух (как оно здесь сформулировано).
В случае, если отображение обратимо (см. ниже), прообраз каждой точки области значений одноточечный, поэтому для обратимых отображений выполняется следующее усиленное свойство для пересечений:
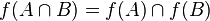 .
.Сюръективность
Функция  называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция
называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция  сюръективна, если образ множества
сюръективна, если образ множества 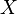 при отображении совпадает с множеством
при отображении совпадает с множеством 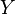 :
: 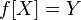 .
.
Такое отображение называется еще отображением на.
Если условие сюръективности нарушается, то такое отображение называют отображением в.
Инъективность
Функция  называется инъективной (или, коротко, инъекция), если разным элементам множества
называется инъективной (или, коротко, инъекция), если разным элементам множества 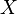 сопоставлены разные элементы множества
сопоставлены разные элементы множества 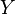 . Более формально, функция
. Более формально, функция  инъективна, если для любых двух элементов
инъективна, если для любых двух элементов 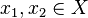 таких, что
таких, что 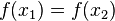 , непременно выполняется
, непременно выполняется 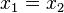 .
.
Другими словами, сюръекция — это когда «у каждого образа есть прообраз», а инъекция — это когда «разные — в разные». То есть при инъекции не бывает так, чтобы два или больше разных элементов 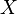 отображались в один и тот же элемент
отображались в один и тот же элемент 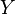 . А при сюръекции не бывает так, чтобы какой-то элемент
. А при сюръекции не бывает так, чтобы какой-то элемент 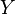 не имел прообраза.
не имел прообраза.
Биективность
Если функция является и сюръективной, и инъективной, то такую функцию называют биективной или взаимно однозначной.
Возрастание и убывание
Монотонная функция
Пусть дана функция 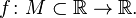 Тогда
Тогда
 называется возраста́ющей на
называется возраста́ющей на 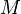 , если
, если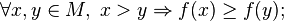
 называется стро́го возраста́ющей на
называется стро́го возраста́ющей на 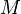 , если
, если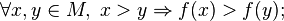
 называется убыва́ющей на
называется убыва́ющей на 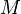 , если
, если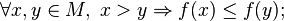
 называется стро́го убыва́ющей на
называется стро́го убыва́ющей на 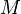 , если
, если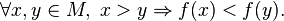
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Периодичность
Функция 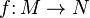 называется периодической с пери́одом
называется периодической с пери́одом  , если справедливо
, если справедливо
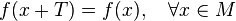 .
.
Если это равенство не выполнено ни для какого 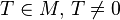 , то функция
, то функция  называется апериоди́ческой.
называется апериоди́ческой.
Четность
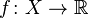 называется нечетной, если справедливо равенство
называется нечетной, если справедливо равенство
 называется четной, если справедливо равенство
называется четной, если справедливо равенство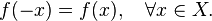
Экстремумы функции
Пусть дана функция 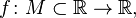 и
и 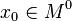 — внутренняя точка области определения
— внутренняя точка области определения 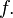 Тогда
Тогда
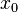 называется точкой абсолютного (глобального) максимума, если
называется точкой абсолютного (глобального) максимума, если
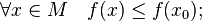
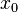 называется точкой абсолютного минимума, если
называется точкой абсолютного минимума, если

В зависимости от того, какова природа области определения и области значений, различают случаи, когда эти области — это:
В первом случае рассматриваются отображения в самом общем виде и решаются наиболее общие вопросы. Таким общим вопросом, например, является вопрос о сравнении множеств по мощности: если между двумя множествами существует взаимно однозначное отображение (биекция), то два данных множества называютэквивалентными или равномощными. Это позволяет провести классификацию множеств в виде единой шкалы, начальный фрагмент выглядит следующим образом:
В соответствии с этим, имеет смысл рассматривать следующие примеры отображений:
Во втором случае, основной объект рассмотрения — заданная на множестве структура и то, что происходит с этой структурой при отображении: если существует взаимно однозначное отображение одной структуры в другую, что при отображении сохраняются свойства заданной структуры, то говорят, что между двумя структурами установлен изоморфизм. Таким образом, изоморфные структуры, заданные в различных множествах, невозможно различить, поэтому в математике принято говорить, что данная структура рассматривается «с точностью до изоморфизма».
Существует великое разнообразие структур, которые могут быть заданы на множествах. Сюда относится:
Природа множеств определяет и свойства соответствующих функций, поскольку эти свойства формулируются в терминах структур, заданных на множествах. Например, свойство непрерывности требует задания топологической структуры.
Частично определенная функция  из множества
из множества 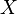 в множество
в множество 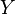 есть функция
есть функция 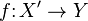 с областью определения
с областью определения 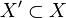 .
.
Некоторые авторы понимают под функцией частично определенную функцию. Это имеет свои преимущества, например возможна запись 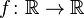 , где
, где 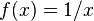 в этом случае
в этом случае  .
.
В силу определения функции, заданному значению аргумента соответствует ровно одно значение функции. Несмотря на это, нередко можно услышать про т. н.«многозначные» функции. В действительности, это не более чем удобное обозначение функции, область значений которой сама является семейством множеств.
Пусть 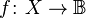 , где
, где  — семейство подмножеств множества
— семейство подмножеств множества 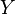 . Тогда
. Тогда 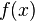 будет множеством для всякого
будет множеством для всякого 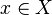 .
.
Функция однозначна, если каждому значению аргумента соответствует единственное значение функции. Функция многозначна, если хотя бы одному значению аргумента соответствует два или более значений функции .
функция Дирихле Необычной является уже сама функция Дирихле, о которой говорилось выше. Ведь на самом маленьком отрезке оси абсцисс бесконечно много и рациональных чисел и иррациональных чисел. Но функция Дирихле для рациональных чисел равна единице, а для иррациональных - нулю. Поэтому когда x пробегает ось абсцисс, то значение функции все время прыгает от 0 к 1 и обратно. Построить график этой функции совершенно невозможно, потому что эта функция во всех точках разрывна.
Но и среди непрерывных функций есть функции с неожиданными свойствами. Например, может ли непрерывная функция иметь на конечном отрезке бесконечно много максимумов и минимумов? На первый взгляд это совершенно невозможно. Ведь функция должна успеть опуститься из точки максимума в точку минимума, потом опять подняться в точку максимума и т. д. Как же ей сделать все это на конечном отрезке? Тем не менее оказалось, что такие странные функции существуют, причем построить их совсем нетрудно.
Построим такую функцию на отрезке [0, 1]. Для этого разделим отрезок пополам и построим на левой половине равносторонний треугольник. Теперь разделим оставшуюся правую половину снова на две равные части и на части [1/2, 3/4] построим второй равносторонний треугольник. Выполним описанную операцию бесконечно много раз. У нас получится "горная цепь", состоящая из бесконечного числа вершин, постепенно опускающаяся к точке 1 (рис. 12). Примем полученную ломаную за график функции f(x). Тогда функция будет определена в каждой точке отрезка [0, 1], за исключением крайней правой точки 1. В этой точке положим f(1) = 0.
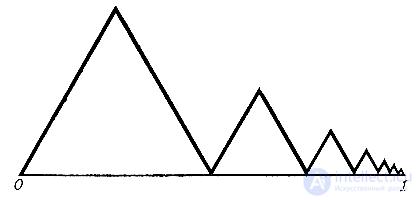
Рис. 12
Так как при приближении к точке 1 высоты вершин стремятся к нулю, полученная нами функция непрерывна во всех точках отрезка [0, 1]. А число максимумов и минимумов на этом отрезке бесконечно велико!
Математику XVIII в., чтобы построить такую странную функцию, понадобилось бы долго комбинировать различные функции, прежде чем он догадался бы, что функция
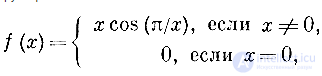
имеет бесконечно много максимумов и минимумов на отрезке [0, 1].
Но функции с бесконечным числом максимумов и минимумов были лишь началом неприятностей, ожидавших математиков. Джинн только начал выходить из бутылки.
"Мокрые точки". У функции, которую мы построили в предыдущем пункте, есть лишь одна точка, около которой бесконечно много максимумов и минимумов, а именно точка 1. Сейчас мы построим другую функцию, у которой таких точек будет куда больше.
Предположим, что на отрезок [0, 1] оси абсцисс падает сверху дождь. Для защиты от дождя поступим следующим образом. Разделим отрезок [0, 1] на три равные части и возведем над средней частью палатку в форме равностороннего треугольника. Она защитит от дождя все точки средней части (кроме концов этой части, то есть точек 1/3 и 2/3). Теперь каждую из оставшихся двух частей снова разделим на три равные части и защитим средние части палатками той же формы (но втрое меньшего размера).
У нас получится линия, изображенная на рис. 13. На третьем шаге процесса мы построим еще четыре палатки, потом еще восемь и т. д.
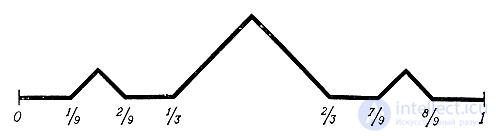
Рис. 13
Возникает вопрос: все ли точки отрезка защищены получившейся пилообразной линией или остались точки, которые дождь намочит? Некоторые из таких "мокрых" точек указать легко - ими являются концы защищаемых отрезков (то есть такие, как 1/3, 2/3, 1/9, 2/9, 7/9, 8/9 и т. д.). Все эти точки остаются без защиты при возведении соответствующей палатки, а последующие палатки их тоже не защищают. Легко видеть, что таких концов будет бесконечное, но счетное множество.
Оказывается, что кроме этого счетного множества "мокрых" точек найдется еще целый континуум таких точек. Чтобы описать их, удобно прибегнуть к троичной системе счисления, в которой все числа записываются с помощью всего лишь трех цифр: 0, 1 и 2. В этой системе счисления число "семь" записывается в виде 21, а дробь 1/4 - в виде 0,02020202... (чтобы убедиться в этом, надо вспомнить правило суммирования геометрической прогрессии).
Теперь мы уже можем точно сказать, какие точки останутся "мокрыми" после того, как все защитные палатки будут построены. Первая палатка защищает точки, лежащие между 1/3 и 2/3. Но это те самые точки, которые в троичной системе имеют запись вида
0,1... ,
где точками обозначена любая комбинация цифр 0, 1 и 2 (точно так же, как в десятичной системе счисления между точками 1/10 и 2/10 лежат все точки, десятичная запись которых начинается с цифры 1, то есть имеет вид 0,1...). После первого шага "мокрыми" останутся точки, троичная запись которых имеет вид
0,0...
или вид
0,2...
Точно так же доказывается, что после возведения двух палаток на втором шаге мокрыми остаются лишь точки, троичная запись которых начинается с одной из следующих четырех комбинаций:

Итак, шаг за шагом защищаются от дождя точки, в троичную запись которых входят единицы. В конце концов останутся "мокрыми" лишь точки, которые можно записать в троичной системе счисления, не используя 1.
А теперь уже ясно, почему множество "мокрых" точек имеет мощность континуума. Ведь это множество можно поставить во взаимно однозначное соответствие с множеством бесконечных телеграмм. Для этого нужно лишь каждой точке вида
0,20220200...
поставить в соответствие бесконечную телеграмму, заменив 0 на точку, а 2 - на тире. При этом разным числам будут соответствовать разные телеграммы. Мы знаем, что множество бесконечных телеграмм имеет мощность континуума. Поэтому и множество "мокрых" точек имеет ту же мощность.
Множество точек, которые мы назвали "мокрыми", впервые построил Кантор, и его называют канторовым множеством. Из построения палаток видно, что около каждой точки канторова множества есть бесконечно много максимумов и минимумов пилообразной линии.
Чертова лестница. С тем же самым канторовым множеством связана еще одна интересная функция. Она строится следующим образом. Снова разделим отрезок [0, 1] на три равные части и положим, что во всех точках средней части наша функция равна 1/2. Потом левую и правую трети снова разделим на три равные части и положим, что от 1/9 до 2/9 функция равна 1/4, а от 7/9 до 8/9 она равна 3/4. Теперь у нас остались четыре отрезка, на которых функция еще не определена:
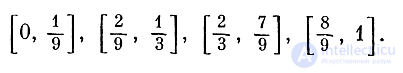
Разделим каждый из них на три равные части и на каждой из средних частей положим функцию равной соответственно
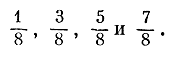
Продолжая этот процесс, мы получим функцию, которая определена во всех "сухих" точках, то есть во всех точках, не принадлежащих канторову множеству. Ее легко определить и в точках этого множества так, чтобы она стала после этого непрерывной и неубывающей. График получившейся функции приближенно изображен на рис. 14. Он имеет вид лестницы с бесконечным числом ступенек (на графике изображены не все ступени).
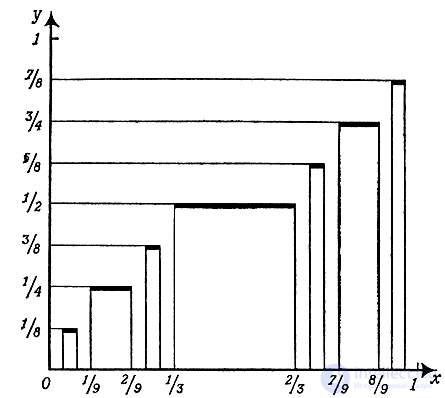
Рис. 14
Впрочем, после того как мы познакомились с линиями, имеющими бесконечно много максимумов и минимумов, лестницей с бесконечным числом ступенек вряд ли кого удивишь. Но удивительно другое. Подсчитаем общую длину всех ступенек нашей лестницы. Первая ступень имеет длину 1/3, две вторые - по 1/9, следующие четыре ступени имеют длину по 1/27 и т. д. Таким образом, сумма длин всех ступеней выражается бесконечной геометрической прогрессией
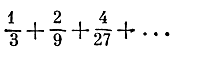
Сумма этой прогрессии равна 1:
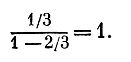
Таким образом, общая длина всех ступеней равна 1.
Но на этих ступеньках функция совсем не поднимается вверх, весь ее подъем сосредоточен в точках канторова множества. А на долю этого множества осталось очень "мало" точек: хотя его мощность и равна континууму, но длина равна нулю! (Длина всего отрезка [0, 1] равна 1, и общая длина ступенек тоже равна 1, так что на долю канторова множества остается лишь нулевая длина.) Таким образом, наша функция умудряется подняться вверх на 1, хотя растет только на множестве нулевой длины и не делает нигде скачков! Не правда ли, удивительно?
Колючая линия. На протяжении многих столетий математики имели дело лишь с линиями, почти в каждой точке которых можно было провести касательную. Если и встречались исключения, то только в нескольких точках. В этих точках линия как бы ломалась, и потому их называли точками излома. Линия, изображенная на рис. 15, а, имеет две точки излома, а линия, изображенная на рис" 15, б,- десять точек излома.
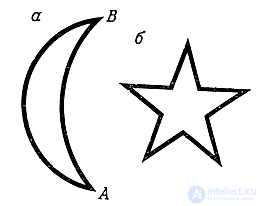
Рис. 15
Но линии, которые мы только что построили, имеют уже бесконечно много точек излома, например линия на рис. 13 ломается во всех точках канторова множества, а кроме того, в вершинах всех треугольников. Однако даже линия на рис. 13 имеет изломы на сравнительно "маленьком" множестве точек, длина которого равна нулю.
В течение долгого времени никто из математиков не верил, что может существовать непрерывная линия, целиком состоящая из зубцов, изломов и колючек. Велико было изумление, когда удалось пои строить такую линию, более того, функцию, график которой был такой колючей изгородью. Первым сделал это Больцано. Но его работа осталась неопубликованной, и впервые такой пример опубликовал Вейерштрасс. Однако пример Вейерштрасса очень трудно изложить - он основан на теории тригонометрических рядов. Пример же Больцано напоминает линии, которые мы строили раньше.
Вот этот пример с небольшими изменениями. Разделим отрезок [0, 1] на четыре равные части и над двумя средними частями построим равнобедренный прямоугольный треугольник (рис. 16, а). Получившаяся линия является графиком некоторой функции, которую обозначим через y = f1(x).
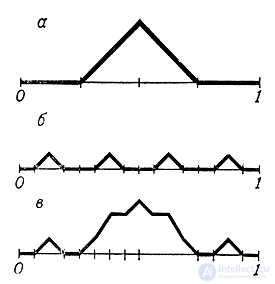
Рис. 16
Разделим теперь каждую из четырех частей еще на четыре равные части и в соответствии с этим построим еще четыре равнобедренных прямоугольных треугольника (рис. 16, б). Мы получим график второй функции y = f2(x). Если сложить эти две функции, то график суммы y = f1(x) + f2(x) будет иметь вид, изображенный на рис. 16, в. Видно, что получившаяся линия имеет уже больше изломов и эти изломы гуще расположены. На следующем шаге мы снова разделим каждую часть еще на четыре части, построим 16 равнобедренных прямоугольных треугольников и прибавим соответствующую функцию y = f3(x) к функции y = f1(x) + f2(x).
Продолжая этот процесс, мы будем получать все более и более изломанные линии. В пределе получится линия, у которой излом в каждой точке и ни в одной точке к ней нельзя провести касательную.

Рис. 17
Похожий пример линии, нигде не имеющей касательной, построил голландский ученый Ван-дер-Варден*. Он взял равносторонний треугольник,разделил каждую его сторону на три равные части и на средних частях построил новые равносторонние треугольники, смотрящие наружу. У него получилась звезда. Теперь каждую из двенадцати сторон этой звезды он разделил еще на три части и снова на каждой из средних частей построил правильный треугольник. Получилась еще более колючая линия, изображенная на рис. 17. После бесконечного числа делений и построений правильных треугольников получилась линия, в каждой точке которой есть излом, колючка.
* (Ван-дер-Варден Бартел (р. 1903) - голландский математик, работал в области алгебры, статистики, истории математики.)
Математики построили много непрерывных функций, графики которых не имели касательной ни в одной точке, и начали изучать их свойства. Эти свойства совсем не походили на свойства "добропорядочных" гладких функций, с которыми они до тех пор имели дело. Поэтому математики, воспитанные в классических традициях, с изумлением смотрели на новые функции. Более того, виднейший представитель классического математического анализа Шарль Эрмит* так писал своему другу, голландскому математику Стилтьесу**. "Я с ужасом отворачиваюсь от этой достойной сожаления язвы непрерывных функций, не имеющих производной ни в одной точке" (то есть, как мы их называли, всюду колючих линий).
* (Эрмит Шарль (1822-1901) - французский математик, автор многочисленных исследований по математическому анализу, алгебре, теории чисел.)
** (Стилтьес Томас (1856-1894) - голландский математик, автор ряда работ по математическому анализу.)
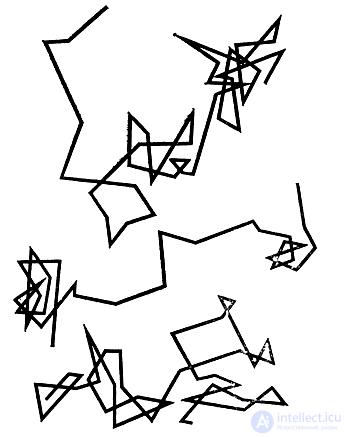
Рис. 18
В физике встречаются линии, очень напоминающие колючие линии Ван-дер-Вардена и других. Это - траектории частиц, совершающих под ударами молекул броуновское движение. Французский ученый Ж. Перрен* сделал; зарисовки движения таких частиц. Он наблюдал их положения через каждые полминуты и соединял полученные точки прямолинейными отрезками. В результате у него получились запутанные ломаные, вроде изображенных на рис. 18. Но не следует думать, что в действительности между отдельными наблюдениями частица двигалась по прямой. Если бы Перрен наблюдал ее не через полминуты, а через полсекунды, то каждый прямолинейный отрезок пришлось бы заменить ломаной, столь же сложной, как и ломаные на рис. 18. И чем меньше были бы промежутки между наблюдениями, тем сложнее и "колючее" становилась бы ломаная. Американский математик Н. Винер** показал, что движение броуновской частицы, настолько малой, что ее инерцией можно пренебречь, совершается по линии, нигде не имеющей касательной.
* (Перрен Жан (1870-1942) - французский физик и физико-химик, экспериментально изучал броуновское движение.)
** (Винер Норберт (1894-1964) - американский ученый, "отец кибернетики". Ряд его работ посвящен функциональному анализу и изучению бесконечномерных пространств.)
Замкнутая линия бесконечной длины. С линиями бесконечной длины мы встречаемся часто - бесконечную длину имеют прямая линия, парабола, гипербола и т. д. Все эти линии уходят в бесконечность, а потому и неудивительно, что их длина бесконечна. Впрочем, нетрудно построить и линию, целиком лежащую в конечной части плоскости, но имеющую бесконечную длину. Для этого надо взять окружность и намотать на нее спираль с бесконечным числом оборотов. Так как число оборотов бесконечно, а длина каждого витка больше длины окружности, то длина всей спирали бесконечна.
Но может ли существовать замкнутая линия бесконечной длины? Обычные замкнутые линии: окружность, эллипс, кардиоида - имеют конечную длину. Длина же колючей линии Ван-дер-Вардена бесконечна.
В самом деле, легко подсчитать, что после n-го шага получается линия, имеющая периметр 3*(4/3n). Но при возрастании n это выражение стремится к бесконечности. Отсюда и вытекает, что длина линии Ван-дер-Вардена бесконечна.
Математический ковер. Рассказывают, что Екатерина II однажды спросила какого-то генерала, в чем разница между мортирой и гаубицей. Растерявшийся генерал ответил: "А видишь ли, государыня-матушка, мортира-то она особь статья, а гаубица - особь статья". Примерно столь же содержательный ответ можно получить, если спросить далекого от математики человека, в чем разница между линией, поверхностью и телом. Более того, он удивится, как можно спрашивать о столь очевидных вещах. Ведь всякому ясно, что линия, поверхность и тело - совсем разные вещи, и никто не назовет окружность поверхностью или сферу линией.
Но один остроумный шахматный гроссмейстер сказал, что разница между мастером и начинающим шахматистом состоит в том, что начинающему все ясно в позиции, где для мастера все полно тайны. Так же обстоит дело и с нашим вопросом. Конечно, относительно таких геометрических фигур, как квадрат или окружность, ни у кого не возникает сомнений, линии они или поверхности. Но в ходе развития науки после открытий Кантора появилось много самых причудливых геометрических фигур, относительно которых не только школьник, но и умудренный знаниями профессор математики не сразу ответит, что это такое - линия, поверхность или тело.
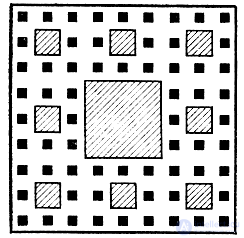
Рис. 19
Вот некоторые из этих фигур. Возьмем квадрат со стороной 1, разделим его на 9 равных квадратиков и выкинем среднюю часть (оставив ее стороны). После этого разделим каждый из оставшихся квадратов снова на 9 равных квадратиков и снова удалим центральные квадратики. Еще один такой шаг приведет к фигуре, изображенной на рис. 19, где заштрихованы все выброшенные квадратики. Ясно, что эта фигура еще является поверхностью. Но мы не остановимся и будем бесконечно много раз делить квадратики на 9 равных частей, после чего выбрасывать среднюю часть. В конце концов у нас получится геометрическая фигура, которую называют ковром Серпинского по имени придумавшего ее польского ученого.
Эта фигура похожа на ткань, сотканную сумасшедшим ткачом. Вдоль и поперек идут нити основы и утка, сплетаясь в очень симметричные и красивые узоры. Но сама получившаяся ткань весьма дырява - ни одного целого куска в ней нет, каждый самый маленький квадратик подвергался вырезанию центральной части. И совсем неясно, чем является этот ковер - линией или поверхностью? Ведь, с одной стороны, он не содержит ни одной целой части, а потому вряд ли является поверхностью, а с другой - образующие его нити сплелись в настолько сложный узор, что вряд ли кто-нибудь без колебаний назовет ковер Серпинского линией. Во всяком случае, нарисовать эту "линию" было бы невозможно.
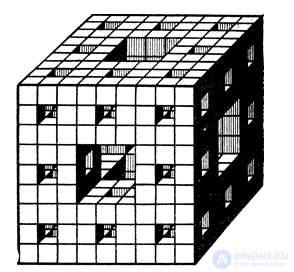
Рис. 20
А ковер Серпинского - не самая сложная из геометрических фигур. Вместо квадрата мы разделим кубик на 27 равных кубиков и выбросим центральный кубик вместе о шестью прилегающими к нему кубиками. После этого разделим каждый оставшийся кубик еще на 27 частей и продолжим операцию выбрасывания (на рис. 20 изображено тело, остающееся после двух выбрасываний). Проделаем эту операцию бесконечно много раз. Чем является оставшаяся после всех выбрасываний геометрическая фигура - линией, поверхностью или телом?
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про функция Надеюсь, что теперь ты понял что такое функция, математическая функция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории введение в математику. основы
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
введение в математику. основы
Термины: введение в математику. основы