Число - основное понятие математики

Сразу хочу сказать, что здесь никакой воды про число, и только нужная информация. Для того чтобы лучше понимать что такое число, натуральные числа, рациональные числа, действительные числа, вещественные числа, комплексные числа , настоятельно рекомендую прочитать все из категории введение в математику. основы.

число — основное понятие математики , используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций. Возникнув еще в первобытном обществе из потребностей счета, понятие числа с развитием науки значительно расширилось.

Основные классы чисел

натуральные числа , получаемые при естественном счете; множество натуральных чисел обозначается 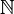. То есть 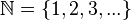(иногда к множеству натуральных чисел также относят ноль, то есть 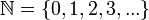). Натуральные числа замкнуты относительно сложения и умножения (но не вычитания илиделения). Сложение и умножение натуральных чисел коммутативны и ассоциативны, а умножение натуральных чисел дистрибутивно относительно сложения и вычитания.

Важным подмножеством натуральных чисел являются простые числа 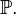Простое число — это натуральное число, имеющее ровно два различных натуральныхделителя: единицу и самого себя. Все остальные натуральные числа, кроме единицы, называются составными. Ряд простых чисел начинается так: 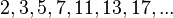Любое натуральное число, большее единицы, представимо в виде произведения степеней простых чисел, причем единственным способом с точностью до порядка следования сомножителей. Например, 121968=2⁴·3²·7·11².

Целые числа, получаемые объединением натуральных чисел с множеством отрицательных чисел и нулем, обозначаются 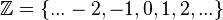. Целые числа замкнуты относительно сложения, вычитания и умножения (но не деления).

рациональные числа — числа, представимые в виде дроби m/n (n≠0), где m — целое число, а n — натуральное число. Рациональные числа замкнуты уже относительно всех четырех арифметических действий: сложения, вычитания, умножения и деления (кроме деления на ноль). Для обозначения рациональных чисел используется знак 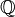(от англ. quotient).

Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных дляматематического анализа) операций предельного перехода. Множество вещественных чисел обозначается 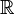. Его можно рассматривать как пополнение поля рациональных чисел 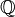при помощи нормы, являющейся обычной абсолютной величиной. Кроме рациональных чисел, 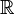включает множество иррациональных чисел 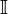, не представимых в виде отношения целых.

комплексные числа 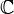, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде 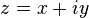, где i — т. н. мнимая единица, для которой выполняется равенство . Комплексные числа используются при решении задач электротехники, гидродинамики, картографии, квантовой механики,теории колебаний, теории хаоса, теории упругости и многих других. Комплексные числа подразделяются на алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим. Более общими (но все еще счетными) классами чисел, чем алгебраические, являются периоды, вычислимые и арифметические числа (где каждый последующий класс шире, чем предыдущий).

Для перечисленных множеств чисел справедливо следующее выражение: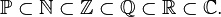

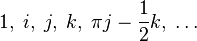Натуральные числа Целые числа Рациональные числа вещественные числа Комплексные числа
	Кватернионы

Обобщения чисел

Кватернионы представляющие собой разновидность гиперкомплексных чисел. Об этом говорит сайт https://intellect.icu . Множество кватернионов обозначается 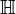. Кватернионы в отличие от комплексных чисел не коммутативны относительно умножения.

В свою очередь октавы 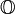, являющиеся расширением кватернионов, уже теряют свойство ассоциативности.

В отличие от октав, седенионы 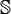не обладают свойством альтернативности, но сохраняют свойство степенной ассоциативности.

Для этих множеств обобщенных чисел справедливо следующее выражение: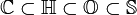

p-адические числа можно рассматривать как элементы поля, являющегося пополнением поля рациональных чисел 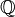при помощи т. н. p-адического нормирования, аналогично тому, как поле действительных чисел 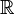определяется как его пополнение при помощи обычной абсолютной величины.

Аде́ли определяются как бесконечные последовательности {a_∞,a₂,a₃,…a_p…}, где a_∞ — любое действительное число, а a_p — p-адическое, причем все a_p, кроме, может быть, конечного их числа, являются целыми p-адическими. Складываются и умножаются адели покомпонентно и образуют кольцо. Поле рациональных чисел вкладывается в это кольцо обычным образом r→{r, r,…r,…}. Обратимые элементы этого кольца образуют группу и называются иде́лями.

Практически важным обобщением числовой системы является интервальная арифметика.

Представление чисел в памяти компьютера

подробнее см. Прямой код, Дополнительный код (представление числа), Число с плавающей запятой

Для представления натурального числа в памяти компьютера, оно обычно переводится в двоичную систему счисления. Для представления отрицательных чисел часто используется дополнительный код числа, который получается путем прибавления единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.

Представление чисел в памяти компьютера имеет ограничения, связанные с ограниченностью объема памяти, выделяемого под числа. Даже натуральные числа представляют собой математическую идеализацию, ряд натуральных чисел бесконечен. На объем же памяти ЭВМ накладываются физические ограничения. В связи с этим в ЭВМ мы имеем дело не с числами в математическом смысле, а с некоторыми их представлениями, или приближениями. Для представления чисел отводится некоторое определенное число ячеек (обычно двоичных, бит — от BInary digiT) памяти. В случае, если в результате выполнения операции полученное число должно занять больше разрядов, чем отводится в ЭВМ, происходит так называемое переполнение, и должна быть зафиксирована ошибка. действительные числа обычно представляются в виде чисел с плавающей запятой. При этом лишь некоторые из действительных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближенными значениями. В наиболее распространенном формате число с плавающей запятой представляется в виде последовательности битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и еще один бит используется для указания знака числа.

История развития понятия

Понятие числа возникло в глубокой древности из практической потребности людей и развивалось в процессе развития человечества. Область человеческой деятельности расширялась и соответственно, возрастала потребность в количественном описании и исследовании. Сначала понятие числа определялось теми потребностями счета и измерения, которые возникали в практической деятельности человека, все более усложняясь. Позже число становится основным понятием математики, и потребности этой науки определяют дальнейшее развитие этого понятия.

Доисторические времена

Считать предметы человек умел еще в глубокой древности, тогда и возникло понятие натурального числа. На первых ступенях развития понятие отвлеченного числа отсутствовало. В те времена человек мог оценивать количества однородных предметов, называемых одним словом, например "три человека", "три топора". При этом использовались разные слова "один" "два", "три" для понятий "один человек", "два человека", "три человека" и "один топор", "два топора", "три топора". Это показывает анализ языков первобытных народностей. Такие именованные числовые ряды были очень короткими и завершались неиндивидуализированным понятием "много". Разные слова для большого количества предметов разного рода существуют и сейчас, такие, как "толпа", "стадо", "куча". Примитивный счет предметов заключался «в сопоставлении предметов данной конкретной совокупности с предметами некоторой определенной совокупности, играющей как бы роль эталона» , которым у большинства народов являлись пальцы ("счет на пальцах"). Это подтверждается лингвистическим анализом названий первых чисел. На этой ступени понятие числа становится не зависящим от качества считаемых объектов.

Появление письменности

Возможности воспроизведения чисел значительно увеличились с появлением письменности. Первое время числа обозначались черточками на материале, служащем для записи, например папирус, глиняные таблички, позже стали применяться другие знаки для больших чисел, о чем ясно свидетельствуют вавилонские клинописные обозначения и сохранившиеся до наших дней "римские цифры". Когда в Индии появилась позиционная система счисления, позволяющая записать любое натуральное число при помощи десяти знаков (цифр), это стало большим достижением человека.

Осознание бесконечности натурального ряда явилось следующим важным шагом в развитии понятия натурального числа. Об этом есть упоминания в трудах Евклида иАрхимеда и других памятниках античной математики 3 века до н. э. В "Началах" Евклид устанавливает безграничную продолжаемость ряда простых чисел. Здесь же Евклид определяет число, как “множество, составленное из единиц” . Архимед в книге "Псаммит" описывает принципы для обозначения сколь угодно больших чисел.

Появление арифметики

Со временем начинают применяться действия над числами, сначала сложение и вычитание, позже умножение и деление. В результате длительного развития сложилось представление об отвлеченном характере этих действий, о независимости количественного результата действия от рассматриваемых предметов, о том, что, например, два предмета и три предмета составляют пять предметов независимо от характера этих предметов. Когда стали разрабатывать правила действий, изучать их свойства и создавать методы решения задач, тогда начинает развиться арифметика — наука о числах. Потребность в изучении свойств чисел как таковых проявляется в самом процессе развития арифметики, становятся понятными сложные закономерности и их взаимосвязи, обусловленные наличием действий, выделяются классы четных и нечетных чисел, простых и составных чисел и так далее. Тогда появляется раздел математики, который сейчас называется теория чисел. Когда было замечено, что натуральные числа могут характеризовать не только количество предметов, но и еще могут характеризовать порядок предметов, расположенных в ряд, возникает понятие порядкового числа. Вопрос об обосновании понятия натурального числа, столь привычного и простого, долгое время в науке не ставился. Только к середине 19 века под влиянием развития математического анализа и аксиоматического метода в математике, назрела необходимость обоснования понятия количественного натурального числа. Введение в употребление дробных чисел было вызвано потребностью производить измерения и стало исторически первым расширением понятия числа.

Введение отрицательных чисел

В Средние века были введены отрицательные числа, с помощью которых стало легче учитывать долг или убыток. Необходимость введения отрицательных чисел была связана с развитием алгебры как науки, дающей общие способы решения арифметических задач, независимо от их конкретного содержания и исходных числовых данных. Необходимость введения в алгебру отрицательного числа возникает уже при решении задач, сводящихся к линейным уравнениям с одним неизвестным. Отрицательные числа систематически применялись при решении задач еще в 6—11 веках в Индии и истолковывались примерно так же, как это делается в настоящее время.

После того, как Декарт разработал аналитическую геометрию, позволившую рассматривать корни уравнения как координаты точек пересечения некоторой кривой с осью абсцисс, что окончательно стерло принципиальное различие между положительными и отрицательными корнями уравнения, отрицательные числа окончательно вошли в употребление в европейской науке.

Введение действительных чисел

Еще в Древней Греции в геометрии было совершено принципиально важное открытие: не всякие точно заданные отрезки соизмеримы, другими словами, не у каждого отрезка длина может быть выражена рациональным числом, например сторона квадрата и его диагональ. В "Началах" Евклида была изложена теория отношений отрезков, учитывающая возможность их несоизмеримости. В Древней Греции умели сравнивать такие отношения по величине, производить над ними арифметические действия в геометрической форме. Хотя греки обращались с такими отношениями, как с числами, они не осознали, что отношение длин несоизмеримых отрезков может рассматриваться как число. Это было сделано в период зарождения современной математики в 17 веке при разработке методов изучения непрерывных процессов и методов приближенных вычислений. И. Ньютон во "Всеобщей арифметике" дает определение понятия действительного числа: "Под числом мы понимаем не столько множество единиц, сколько отвлеченное отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу". Позже, в 70 годах 19 века, понятие действительного числа было уточнено на основе анализа понятия непрерывности Р. Дедекиндом, Г. Кантором и К. Вейерштрассом.

Введение комплексных чисел

С развитием алгебры возникла необходимость введения комплексных чисел, хотя недоверие к закономерности пользования ими долго сохранялось и отразилось в сохранившемся до сих пор термине "мнимое" . Уже у итальянских математиков 16 века (Дж. Кардано, Р. Бомбелли), в связи с открытием алгебраического решения уравнений третьей и четвертой степеней, возникла идея комплексного числа. Дело в том, что даже решение квадратного уравнения, в том случае, если уравнение не имеет действительных корней, приводит к действию извлечения квадратного корня из отрицательного числа. Казалось, что задача, приводящаяся к решению такого квадратного уравнения, не имеет решения. С открытием алгебраического решения уравнений третьей степени обнаружилось, что в том случае, когда все три корня уравнения являются действительными, по ходу вычисления оказывается необходимо выполнить действие извлечения квадратного корня из отрицательных чисел. После установления в конце 18 века геометрического истолкования комплексных чисел в виде точек на плоскости и установления несомненной пользы от введения комплексных чисел в теории алгебраических уравнений, в особенности после знаменитых работ Л. Эйлера и К. Гаусса, комплексные числа были признаны математиками и начали играть существенную роль не только в алгебре, но и в математическом анализе. Значение комплексных чисел особенно возросло в 19 веке в связи с развитием теории функций комплексного переменного.

Число в философии

Философское понимание числа заложили пифагорейцы. Аристотель свидетельствует, что пифагорейцы считали числа «причиной и началом» вещей, а отношения чисел основой всех отношений в мире. Числа придают миру упорядоченность и делают его космосом. Такое отношение к числу было принято Платоном, а позже неоплатониками. Платон при помощи чисел различает подлинное бытие (то, что существует и мыслится само по себе), и неподлинное бытие, (то, что существует лишь благодаря другому и познается только в отношении). Срединное положение между ними занимает число. Оно придает меру и определенность вещам и делает их причастными бытию. Благодаря числу вещи могут быть подвергнуты пересчету и поэтому они могут быть мыслимы, а не только ощущаемы. Неоплатоники, особенно Ямвлих и Прокл, почитали числа столь высоко, что даже не считали их сущими — устроение мира исходит от числа, хотя и не непосредственно. Числа сверхсущны, пребывают выше Ума, и недоступны знанию. Неоплатоники различают божественные числа (прямую эманацию Единого) и математические числа (составленные из единиц). Последние являются несовершенными подобиями первых. Аристотель, наоборот, приводит целый ряд аргументов, показывающих, что утверждение о самостоятельном существовании чисел приводит к нелепостям. Арифметика выделяет в этих реально сущих вещах только один аспект и рассматривает их с точки зрения их количества. Числа и их свойства являются результатом такого рассмотрения. Кант считал, что явление познано тогда, когда оно сконструировано в соответствии с априорными понятиями — формальными условиями опыта. Число — одно из таких условий. Число задает конкретный принцип или схему конструирования. Любой объект является исчислимым и измеряемым, потому что он сконструирован по схеме числа (или величины). Поэтому всякое явление может рассматриваться математикой. Разум воспринимает природу подчиненной числовым закономерностям именно потому, что сам строит ее в соответствии с числовыми закономерностями. Так объясняется возможность применения математики в изучении природы. Математические определения, разработанные в 19 веке, были серьезно пересмотрены в начале 20 века. Это было вызвано не столько математическими, сколько философскими проблемами. Определения, которые были даны Пеано, Дедекиндом или Кантором, и которые используются в математике и в настоящее время, нужно было обосновать с помощью фундаментальных принципов, коренящихся в самой природе знания. Различают три таких философско-математических подхода: логицизм, интуиционизм и формализм. Философскую базу логицизма разработал Рассел. Он полагал, что истинность математических аксиом неочевидна. Истинность обнаруживается сведением к наиболее простым фактам. Отражением таких фактов Рассел считал аксиомы логики, которые он положил в основу определения числа. Важнейшим понятием у него является понятие класса. Натуральное число η есть класс всех классов, содержащих η элементов. Дробь — это уже не класс, а отношение классов. Интуицист Брауэр имел противоположную точку зрения: логику он считал лишь абстракцией от математики, рассматривал натуральный ряд чисел как базовую интуицию, лежащую в основании всякой мыслительной деятельности. Гильберт, главный представитель формальной школы, видел обоснование математики в построении непротиворечивой аксиоматической базы, в пределах которой можно бы было формально обосновать любое математическое понятие. В разработанной им аксиоматической теории действительных чисел представление о числе лишается всякой глубины и сводится лишь к графическому символу, подставляемому по определенным правилам в формулы теории.

Вау!! 😲 Ты еще не читал? Это зря!

• Системы наименования чисел
• Обратное число
• Псевдослучайное число
• Алгебраические числа
• Нумерология
• Арифметика

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про число Надеюсь, что теперь ты понял что такое число, натуральные числа, рациональные числа, действительные числа, вещественные числа, комплексные числа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории введение в математику. основы