Привет, сегодня поговорим про бпф по основанию с прореживанием по времени, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
бпф по основанию с прореживанием по времени , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
Содержание
Введение
Разбиение исходной последовательности прореживанием по времени
Процедура объединения. Граф «Бабочка»
Граф алгоритма БПФ с прореживанием по времени. Двоично-инверсная перестановка
Поворотные коэффициенты
Вычислительная эффективность алгоритма БПФ с прореживанием по времени
Выводы
Введение
Ранее были приведены выражения для ДПФ и схема процедуры разбиения-объединения. Они потребуются нам для дальнейшего изложения, поэтому приведем их без пояснений.
Выражение для ДПФ имеет вид:
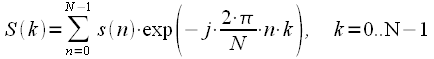 |
(1) |
Процедура разбиения-объединения представлена на рисунке 1.
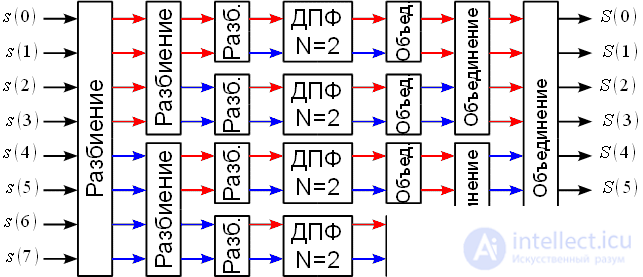
Рисунок 1: Разбиение и объединение последовательностей при N = 8
Разбиение исходной последовательности прореживанием по времени
Для начала комплексную экспоненту в выражении (1) обозначим как:
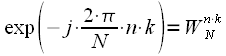 |
(2) |
Тогда выражение (1) принимает вид:
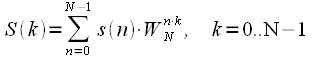 |
(3) |
Прореживание по времени заключается в разбиении исходной последовательности отсчетов
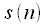
,
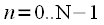
на две последовательности длительности
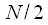

и

,
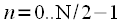
, таких что
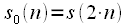
, а
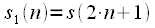
,
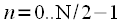
. Другими словами, последовательность

содержит отсчеты последовательности
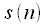
с четными индексами, а

- с нечетными. Прореживание по времени для N = 8 наглядно представлено на рисунке 2.
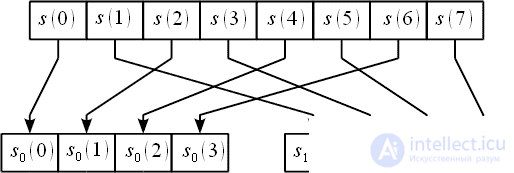
Рисунок 2: Прореживание по времени для N=8
Рассмотрим ДПФ сигнала прореженного по времени:
 |
(4) |
Если рассмотреть только первую половину спектра
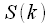
,
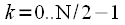
, а также учесть что
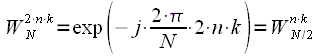 , , |
(5) |
тогда (4) можно записать:
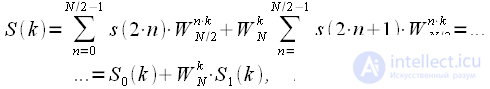 |
(6) |
где
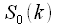
и
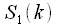
,
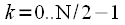
–
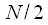
точечные ДПФ последовательностей «четной»

и «нечетной»

,
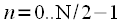
:
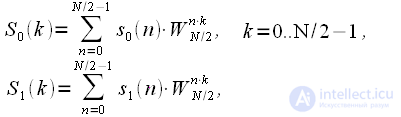 |
(7) |
И что же мы получили? Прореживание по времени можно считать алгоритмом разбиения последовательности на две половинной длительности. Первая половина объединенного спектра есть сумма спектра «четной» последовательности и спектра «нечетной» последовательности, умноженного на коэффициенты
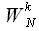
, которые носят названия поворотных коэффициентов.
Процедура объединения. Граф «Бабочка»
Теперь рассмотрим вторую половину спектра

,
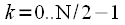
:
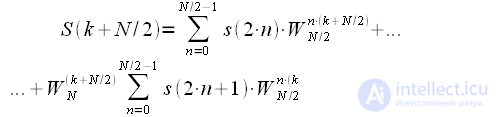 |
(8) |
Рассмотрим подробнее множитель
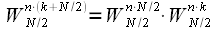 . . |
(9) |
Учтем что
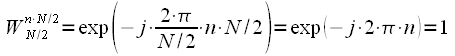 , , |
(10) |
тогда выражение (10) справедливо для любого целого
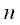
, тогда (9) можно записать с учетом (10):
 . . |
(11) |
Рассмотрим теперь поворотный коэффициент в (8):
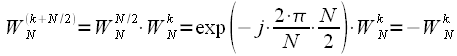 . . |
(12) |
Тогда выражение (8) с учетом (11) и (12) принимает вид:
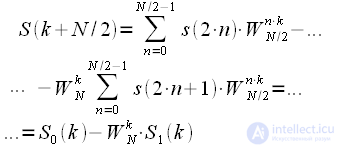 |
(13) |
Таким образом окончательно можно записать:
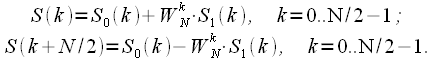 |
(14) |
Выражение (14) представляет собой алгоритм объединения при прореживании по времени. Об этом говорит сайт https://intellect.icu . Данную процедуру объединения можно представить в виде графа (рисунок 3), который называется «Бабочка».
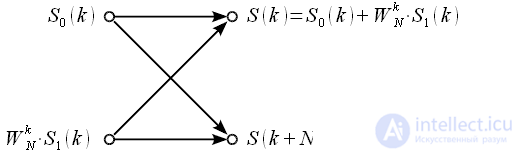
Рисунок 3: Процедура объединения на основе графа « Бабочка »
Граф алгоритма БПФ с прореживанием по времени. Двоично-инверсная перестановка
Представим в виде графа алгоритм БПФ с прореживанием по времени основанный на разбиении — объединении при
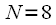
(рисунок 1).
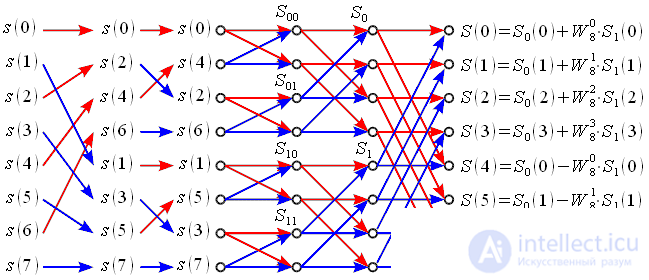
Рисунок 4: Граф алгоритма БПФ с прореживанием по времени при N=8
На первом этапе отсчеты входного сигнала переставляются местами и исходная последовательность делится на «четную» и «нечетную последовательности» (обозначены красными и синими стрелками). Потом «четная» и «нечетная» последовательности в свою очередь делятся на «четную» и «нечетную» последовательности. При
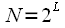
такое деление можно делать
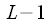
раз. В нашем случае
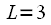
. Данная процедура называется двоично-инверсной перестановкой, так можно выполнить перенумерацию отсчетов переписав номер отсчета в двоичной системе в обратном направлении. Например
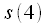
имеет индекс в десятичной системе счисления
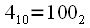
, если же
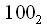
переписать справа налево то получим

, то есть
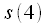
после разбиения на четные нечетные перед первой операцией «Бабочка» встанет на место
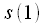
, которая в свою очередь встанет на место
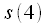
. По аналогичному правилу поменяются местами все отсчеты, при этом некоторые останутся на месте, в частности
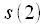
, так как если
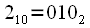
переписать справа налево то все равно останется
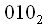
, аналогично
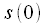
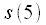
и
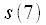
. Очень важно понять, что данный метод перенумерации должен применяться при записи числа в двоичной системе состоящей из
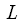
разрядов. В приведенном примере использовалось 3 разряда двоичного числа, но если же
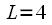
(
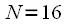
), то необходимо записать число при использовании 4 разрядов. В этом случае
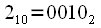
и после переписывания получим
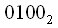
, то есть при
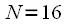
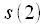
не останется на месте, а поменяется местами с
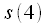
.
Можно сказать что напрямую двоично-инверсная перестановка удобна когда заранее количество отсчетов входного сигнала фиксировано, однако в универсальных алгоритмах БПФ на различные размеры
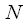
, двоично-инверсная перестановка не эффективна, проще и быстрее поменять отсчеты местами.
После двоично-инверсной перестановки получаем четыре 2-точечных ДПФ:
 |
(15) |
На основе четырех 2-точечных ДПФ формируются два 4-точечных ДПФ:
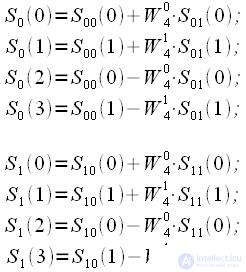 |
(16) |
И на последнем уровне формируется полный спектр входного сигнала.
Поворотные коэффициенты
Рассмотрим подробнее поворотные коэффициенты
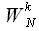
.
На первом уровне (выражение (15)) требуется всего один поворотный коэффициент

, это означает что на первом уровне расчета спектра операции умножения не требуются (умножения на
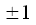
называются тривиальными, так как при умножении на
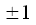
множитель остается неизменным или меняет свой знак на противоположный).
На втором уровне имеем два поворотных коэффициента:
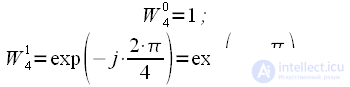 |
(17) |
Умножение на мнимую единицу также можно считать тривиальным, так как реальные и мнимые части комплексного числа просто меняются местами и изменяют свой знак.
На третьем уровне имеем уже 4 поворотных коэффициента:
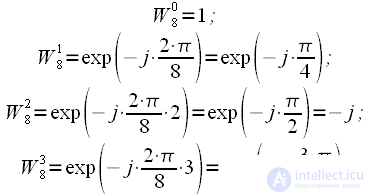 |
(18) |
Графически поворотные коэффициенты можно представить как векторы на комплексной плоскости:

Рисунок 5: Поворотные коэффициенты алгоритма БПФ с прореживанием по времени при N=8
Можно заметить что на всех уровнях объединения количество поворотных коэффициентов удваивается, причем все поворотные коэффициенты предыдущего уровня объединения присутствуют и на следующем уровне. Таким образом для того чтобы перейти на следующий уровень необходимо между поворотными коэффициентами текущего уровня вставить поворотные коэффициенты следующего. Графически для перехода на следующий уровень при N =16 необходимо дополнить рисунок 5 как это показано на рисунке 6. Серые вектора показывают поворотные коэффициенты которые будут присутствовать на последнем уровне при
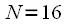
, которых нет при
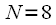
.
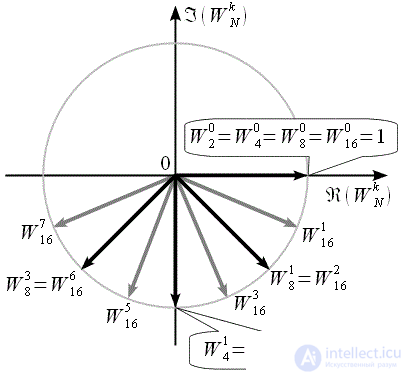
Рисунок 6: Поворотные коэффициенты алгоритма БПФ с прореживанием по времени при N=16
Необходимо также отметить, что все поворотные коэффициенты за исключением нулевого
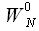
находятся в нижней полуплоскости комплексной плоскости.
Вычислительная эффективность алгоритма БПФ с прореживанием по времени
Алгоритм с прореживанием по времени на каждом уровне требует
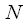
комплексных умножений и сложений. При
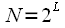
количество уровней разложения — объединения равно
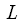
, таким образом общее количество операций умножения и сложения равно
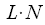
.
Рассмотрим во сколько раз алгоритм БПФ с прореживанием по времени эффективнее ДПФ. Для этого рассмотрим коэффициент ускорения
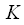
отношение количества комплексных умножение и сложений при использовании ДПФ и БПФ, при этом учтем что

:
 раз. раз. |
(19) |
В таблице ниже приведено требуемое количество операций

для алгоритма ДПФ при различном
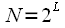
и при использовании БПФ с прореживанием по времени.
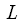 |
4 |
6 |
8 |
10 |
12 |
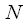 |
16 |
64 |
256 |
1024 |
4096 |
 ДПФ ДПФ |
256 |
4096 |
65536 |
1048576 |
16777216 |
 БПФ БПФ |
64 |
384 |
2048 |
10240 |
49152 |
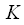 , раз , раз |
4 |
10,7 |
32 |
102,4 |
341 |
Из таблицы хорошо видно, что использование БПФ приводит к существенному уменьшению требуемого количества вычислительных операций. Так например при
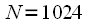
БПФ требует в 100 раз меньше операций чем ДПФ, а при
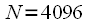
в 341 раз! Первое опубликование данных результатов произвело эффект разорвавшийся бомбы, всколыхнув всю научную общественность. При этом очень важно, что выигрыш по производительности тем больше, чем больше размер выборки
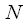
. Так например при
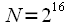
выигрыш составит

раз.
Выводы
Таким образом, для получения эффективного алгоритма БПФ по основанию 2 с прореживанием по времени, при
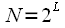
необходимо:
-
Осуществить двоично-инверсную перестановку отсчетов входного сигнала, тем самым обеспечив разбиение последовательности.
-
Используя поворотные коэффициенты сделать N/2 операций «Бабочка» согласно выражению (14) для получения первого объединения
-
Повторить операцию «Бабочка» согласно выражению (14) для объединения на следующий уровень еще
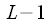
раз, также используя поворотные коэффициенты.
На выходе получим ДПФ входной последовательности.
Надеюсь, эта статья про бпф по основанию с прореживанием по времени, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое бпф по основанию с прореживанием по времени
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Цифровая обработка сигналов
Из статьи мы узнали кратко, но содержательно про бпф по основанию с прореживанием по времени
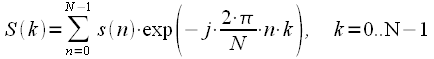

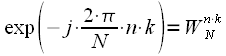
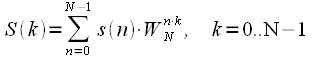
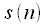 ,
, 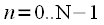 на две последовательности длительности
на две последовательности длительности 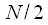
 и
и  ,
, 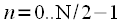 , таких что
, таких что 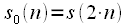 , а
, а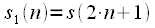 ,
, 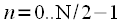 . Другими словами, последовательность
. Другими словами, последовательность  содержит отсчеты последовательности
содержит отсчеты последовательности 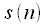 с четными индексами, а
с четными индексами, а  - с нечетными. Прореживание по времени для N = 8 наглядно представлено на рисунке 2.
- с нечетными. Прореживание по времени для N = 8 наглядно представлено на рисунке 2.

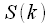 ,
, 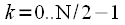 , а также учесть что
, а также учесть что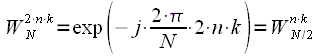 ,
,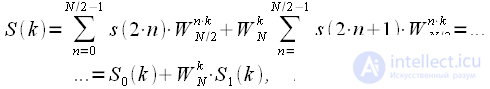
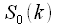 и
и 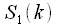 ,
, 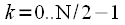 –
– 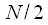 точечные ДПФ последовательностей «четной»
точечные ДПФ последовательностей «четной»  и «нечетной»
и «нечетной»  ,
, 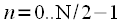 :
: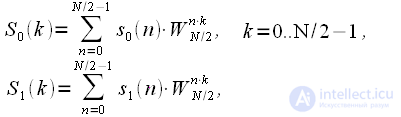
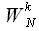 , которые носят названия поворотных коэффициентов.
, которые носят названия поворотных коэффициентов. ,
, 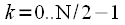 :
: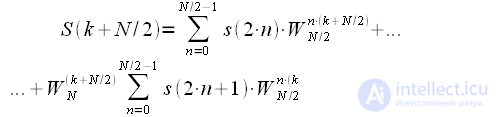
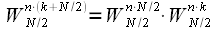 .
.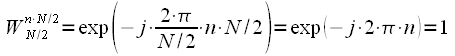 ,
,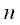 , тогда (9) можно записать с учетом (10):
, тогда (9) можно записать с учетом (10): .
.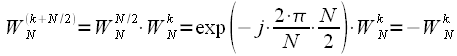 .
.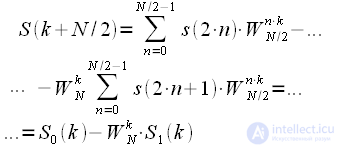
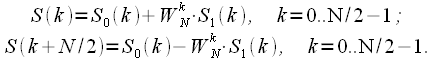

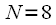 (рисунок 1).
(рисунок 1).
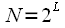 такое деление можно делать
такое деление можно делать 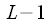 раз. В нашем случае
раз. В нашем случае 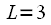 . Данная процедура называется двоично-инверсной перестановкой, так можно выполнить перенумерацию отсчетов переписав номер отсчета в двоичной системе в обратном направлении. Например
. Данная процедура называется двоично-инверсной перестановкой, так можно выполнить перенумерацию отсчетов переписав номер отсчета в двоичной системе в обратном направлении. Например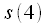 имеет индекс в десятичной системе счисления
имеет индекс в десятичной системе счисления 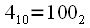 , если же
, если же 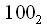 переписать справа налево то получим
переписать справа налево то получим  , то есть
, то есть 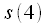 после разбиения на четные нечетные перед первой операцией «Бабочка» встанет на место
после разбиения на четные нечетные перед первой операцией «Бабочка» встанет на место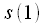 , которая в свою очередь встанет на место
, которая в свою очередь встанет на место 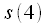 . По аналогичному правилу поменяются местами все отсчеты, при этом некоторые останутся на месте, в частности
. По аналогичному правилу поменяются местами все отсчеты, при этом некоторые останутся на месте, в частности 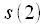 , так как если
, так как если 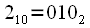 переписать справа налево то все равно останется
переписать справа налево то все равно останется 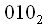 , аналогично
, аналогично 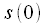
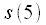 и
и 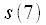 . Очень важно понять, что данный метод перенумерации должен применяться при записи числа в двоичной системе состоящей из
. Очень важно понять, что данный метод перенумерации должен применяться при записи числа в двоичной системе состоящей из 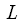 разрядов. В приведенном примере использовалось 3 разряда двоичного числа, но если же
разрядов. В приведенном примере использовалось 3 разряда двоичного числа, но если же 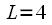 (
(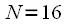 ), то необходимо записать число при использовании 4 разрядов. В этом случае
), то необходимо записать число при использовании 4 разрядов. В этом случае 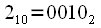 и после переписывания получим
и после переписывания получим 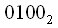 , то есть при
, то есть при 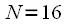
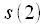 не останется на месте, а поменяется местами с
не останется на месте, а поменяется местами с 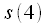 .
.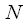 , двоично-инверсная перестановка не эффективна, проще и быстрее поменять отсчеты местами.
, двоично-инверсная перестановка не эффективна, проще и быстрее поменять отсчеты местами.
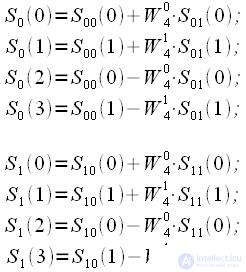
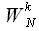 .
. , это означает что на первом уровне расчета спектра операции умножения не требуются (умножения на
, это означает что на первом уровне расчета спектра операции умножения не требуются (умножения на 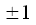 называются тривиальными, так как при умножении на
называются тривиальными, так как при умножении на 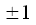 множитель остается неизменным или меняет свой знак на противоположный).
множитель остается неизменным или меняет свой знак на противоположный).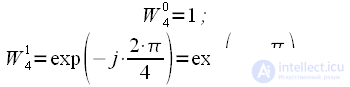
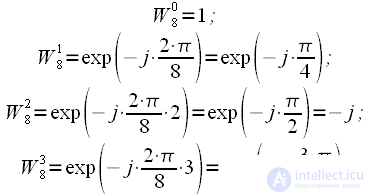

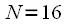 , которых нет при
, которых нет при 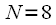 .
.
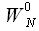 находятся в нижней полуплоскости комплексной плоскости.
находятся в нижней полуплоскости комплексной плоскости.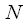 комплексных умножений и сложений. При
комплексных умножений и сложений. При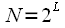 количество уровней разложения — объединения равно
количество уровней разложения — объединения равно 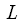 , таким образом общее количество операций умножения и сложения равно
, таким образом общее количество операций умножения и сложения равно 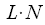 .
.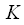 отношение количества комплексных умножение и сложений при использовании ДПФ и БПФ, при этом учтем что
отношение количества комплексных умножение и сложений при использовании ДПФ и БПФ, при этом учтем что  :
: раз.
раз. для алгоритма ДПФ при различном
для алгоритма ДПФ при различном 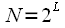 и при использовании БПФ с прореживанием по времени.
и при использовании БПФ с прореживанием по времени.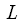
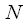
 ДПФ
ДПФ БПФ
БПФ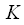 , раз
, раз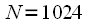 БПФ требует в 100 раз меньше операций чем ДПФ, а при
БПФ требует в 100 раз меньше операций чем ДПФ, а при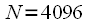 в 341 раз! Первое опубликование данных результатов произвело эффект разорвавшийся бомбы, всколыхнув всю научную общественность. При этом очень важно, что выигрыш по производительности тем больше, чем больше размер выборки
в 341 раз! Первое опубликование данных результатов произвело эффект разорвавшийся бомбы, всколыхнув всю научную общественность. При этом очень важно, что выигрыш по производительности тем больше, чем больше размер выборки 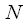 . Так например при
. Так например при 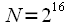 выигрыш составит
выигрыш составит  раз.
раз.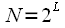 необходимо:
необходимо: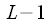 раз, также используя поворотные коэффициенты.
раз, также используя поворотные коэффициенты.
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов