Лекция
Привет, сегодня поговорим про кратчайший путь, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое кратчайший путь, алгоритмы поиска кратчайшего пути, поиск пути , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
поиск пути (англ. Pathfinding) — термин в информатике и искусственном интеллекте, который означает определение компьютерной программой наилучшего, оптимального маршрута между двумя точками.
Задача о поиске кратчайшего пути это — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов ребер, составляющих путь.
Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для ее решения[⇨].
У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.
Значимость данной задачи определяется ее различными практическими применениями[⇨]. Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между точкой отправления и точкой назначения. В качестве вершин выступают перекрестки, а дороги являются ребрами, которые лежат между ними. Если сумма длин дорог между перекрестками минимальна, тогда найденный путь самый короткий.
В задаче о кратчайшем пути (shortest-paths problem) задается взвешенный ориентированный граф G = (V, Е) с весовой функцией w : Е —> R, отображающей ребра на их веса, значения которых выражаются действительными числами. Вес (weight) пути р = (Vo, Vi,..., Vk) равен суммарному весу входящих в него ребер.
Вес кратчайшего пути (shortest-path weight) из вершины и в вершину v определяется соотношением
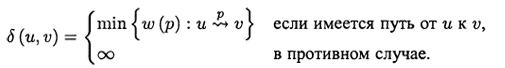
Тогда по определению
кратчайший путь (shortest path) из вершины и в вершину v — это любой путь, вес которого удовлетворяет соотношению w (р) = delta(u, v).
Вес каждого из ребер можно интерпретировать не как расстояние, а как другую метрику. Часто они используются для представления временных интервалов, стоимости, штрафов, убытков или любой другой величины, которая линейно накапливается по мере продвижения вдоль ребер графа и которую нужно свести к минимуму.
Алгоритм позволяет решить многие другие задачи, в том числе те, что перечислены ниже.
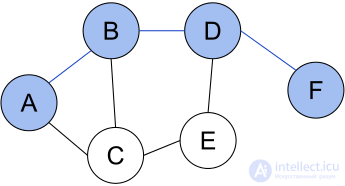
Рис 1 Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.

Рис 2 Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.
Поиск пути в контексте компьютерных игр касается пути, на котором движущийся объект ищет путь вокруг препятствий. Наиболее часто задача поиска пути возникает в стратегиях реального времени, в которых игрок дает задание игровым юнитам (единицам) двигаться через игровой уровень, который содержит препятствия. Кроме стратегий, задача поиска пути, так или иначе, в той или иной мере встречается в большинстве современных игровых жанров. Так как игры становятся все сложнее, то поиск пути также эволюционирует и развивается вместе с ними.
Стратегии реального времени обычно содержат большие территории с открытым ландшафтом, в которых поиск пути обычно является простой задачей. Однако в большинстве случаев по карте перемещается не один юнит, а несколько, что создает потребность в различных и намного более сложных алгоритмах поиска пути для избежания пробок в узких областях игрового ландшафта. В стратегиях игровой уровень делится на тайлы (англ. tiles), которые действуют как узлы (англ. nodes) в алгоритме поиска пути .
В жанре 3D-шутеров используются намного более ограниченные пространства, которые не так легко разделить на узлы. Здесь взамен узлов используются так называемые waypoints (дословно с англ. — «точки пути»). Waypoints — это нерегулярные и вручную установленные узлы, которые содержат информацию о том, к каким другим узлам возможно добраться от данного.
Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.
Граф представляет собой совокупность непустого множества вершин и ребер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин , таких что
смежна с
для
. Такой путь
называется путем длиной
из вершины
в
(
указывает на номер вершины пути и не имеет никакого отношения к нумерации вершин на графе).
Пусть — ребро соединяющее две вершины:
и
. Дана весовая функция
, которая отображает ребра на их веса, значения которых выражаются действительными числами, и неориентированный граф
. Об этом говорит сайт https://intellect.icu . Тогда кратчайшим путем из вершины
в вершину
будет называться путь
(где
и
), который имеет минимальное значение суммы
Если все ребра в графе имеют единичный вес, то задача сводится к определению наименьшего количества обходимых ребер.
Существуют различные постановки задачи о кратчайшем пути:
В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объем затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).
Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи . Примеры таких задач:
По своей сути алгоритм поиска пути ищет на графе, начиная с одной (стартовой) точки и исследуя смежные узлы до тех пор, пока не будет достигнут узел назначения (конечный узел). Кроме того, в алгоритмах поиска пути в большинстве случаев заложена также цель найти самый короткий путь. Некоторые методы поиска на графе, такие как поиск в ширину, могут найти путь, если дано достаточно времени. Другие методы, которые «исследуют» граф, могут достичь точки назначения намного быстрее. Здесь можно привести аналогию с человеком, идущим через комнату. Человек может перед началом пути заранее исследовать все характеристики и препятствия в пространстве, вычислить оптимальный маршрут и только тогда начать непосредственное движение. В другом случае человек может сразу пойти в приблизительном или предполагаемом направлении цели и потом, уже во время пути, делать корректировки своего движения для избегания столкновений с препятствиями.
К самым известным и популярным алгоритмам поиска пути относятся такие алгоритмы
В связи с тем, что существует множество различных постановок данной задачи, есть наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:
1) Задача о кратчайшем пути в заданный пункт назначения (single-destination shortest-paths problem). Требуется найти кратчайший путь в заданную вершину назначения (destination vertex) t, который начинается в каждой из вершин v. Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине.
2) Задача о кратчайшем пути между заданной парой вершин (single-pair shortest-paths problem). Требуется найти кратчайший путь из заданной вершины u в заданную вершину v. Если решена задача о заданной исходной вершине u, то эта задача тоже решается.
3) Задача о кратчайшем пути между всеми парами вершин (all-pairs shortest-paths problem). Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.
В работе (Черкасский и др., 1993) представлено еще несколько алгоритмов для решения этой задачи.
В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.
| Алгоритм | Сложность | Автор |
|---|---|---|
| Поиск в ширину | O(E) |
| Алгоритм | Сложность | Автор |
|---|---|---|
| - | O(V2EL) | Форд 1956 |
| Алгоритм Беллмана — Форда | O(VE) | Беллман 1958 , Мур 1957 |
| - | O(V2 log V) | Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960 |
| Алгоритм Дейкстры со списком. | O(V2) | Leyzorek et al. 1957 , Дейкстра 1959 |
| Алгоритм Дейкстры с модифицированной двоичной кучей | O((E + V) log V) | - |
| . . . | . . . | . . . |
| Алгоритм Дейкстры с использованием фибоначчиевой кучи | O(E + V log V) | Фридман&Тарьян 1984 , Фридман&Тарьян 1987 |
| - | O(E log log L) | Джонсон 1982, Карлссон&Поблете 1983 |
| Алгоритм Габова | O(E logE/V L) | Габов 1983, Габов 1985 |
| - | O(E + V√log L) | Ахуджа et al. 1990 |
| Алгоритм | Сложность | Автор |
|---|---|---|
| Алгоритм Беллмана — Форда | O(VE) | Беллман , Мур |
Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году , который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V4).
Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V3), и Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V2 log V).
Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций .
Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере[17].
Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применен для поиска решения с минимальным количеством ходов.
Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.
Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса ребер могут соответствовать протяженности данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях[18].
Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах. Подобные алгоритмы состоят из двух этапов:
Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды[19].
Другие подходы (техники), которые применяются в данной сфере:
Существуют задачи, которые похожи на задачу поиска кратчайшего пути на графе.
Пусть дан направленный граф (V, A), где V — множество вершин и A — множество ребер, с начальной вершиной обхода s, конечной t и весами wij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы xij.
Тогда задача ставится следующим образом: найти минимум функции , где
, при условии что для всех i и j выполняется следующее неравенство:
На этом все! Теперь вы знаете все про кратчайший путь, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое кратчайший путь, алгоритмы поиска кратчайшего пути, поиск пути и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов