Лекция
Привет, сегодня поговорим про целочисленное программирование, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое целочисленное программирование, метод отсекающих плоскостей, метод гомори, метод ветвей и границ , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
Общая постановка задачи целочисленного программирования отличается от общей задачи ЛП лишь наличием дополнительного ограничения. Этим ограничением является требование целочисленности: значения всех или части переменных модели в оптимальном решении являются целыми неотрицательными числами, то есть принадлежат множеству N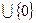 . Если это требование распространяется на все переменные, то задачу ЦП называют полностью целочисленной задачей. Если оно относится лишь к части переменных, задача называется частично целочисленной. Задача ЛП, отличающаяся от задачи ЦП лишь отсутствие требований целочисленности, называют задачей с ослабленными ограничениями, соответствующей данной задаче ЦП.
. Если это требование распространяется на все переменные, то задачу ЦП называют полностью целочисленной задачей. Если оно относится лишь к части переменных, задача называется частично целочисленной. Задача ЛП, отличающаяся от задачи ЦП лишь отсутствие требований целочисленности, называют задачей с ослабленными ограничениями, соответствующей данной задаче ЦП.
Задача целочисленного программирования — это задача математической оптимизации или выполнимости, в которой некоторые или все переменные должны быть целыми числами . Часто термин адресуется к целочисленному линейному программированию (ЦЛП), в котором целевая функция и ограничения (за исключением требования целочисленности) линейны.
Целочисленное программирование является NP-трудной задачей. Специальный случай, 0-1 целочисленное линейное программирование, в которой переменные принимают значения 0 или 1, является одной из 21 NP-полных задач Карпа.
Задача целочисленного линейного программирования в каноническом виде выражается как
| максимизировать | |
| при условиях | |
| и |
а в стандартном виде
| максимизировать | |
| при условиях | |
| и |
где — векторы, а
— матрица, все элементы которых являются целыми числами. Заметьте, что, как и в случае линейного программирования, ЦЛП-задача, не находящаяся в стандартном виде, может быть приведена к стандартному виду путем исключения неравенств введением дополнительных и искусственных переменных и заменой переменных, на которые не наложено ограничение неотрицательности, двумя переменными.
Рисунок справа показывает следующую задачу.
Допустимые целые точки показаны красным и красные пунктирные линии показывают выпуклую оболочку этих точек, которая является наименьшим многоугольником, содержащим все эти точки. Синие линии вместе с координатными осями определяют многоугольник линейного ослабления, который задается неравенствами без требования целочисленности. Цель оптимизации — сдвинуть черную пунктирную линию так, чтобы она была как можно выше, но касалась многоугольника. Оптимальные решения целочисленной задачи — точки и
, на которых целевая функция принимает значение 2. Единственное решение ослабленной (линейной) задачи — точка
, в которой целевая функция принимает значение 2.8. Заметим, что если мы округлим решение задачи линейного программирования до ближайших целых, решение будет недопустимо для ЦЛП.
Следующее рассуждение является сведением задачи минимизации вершинного покрытия к задаче целочисленного программирования, что доказывает NP-трудность.
Пусть — неориентированный граф. Определим задачу линейного программирования следующим образом:
Если наложить требование, чтобы принимали значения 0 или 1, любое допустимое решение для целочисленного программирования является подмножество вершин. Из первого ограничения следует, что по меньшей мере один конец каждого ребра включена в подмножество. Таким образом, решение дает покрытие вершин. Кроме того, если задано вершинное покрытие C,
можно присвоить значение 1 для любого
и 0 для любого
, что дает нам допустимое решение задачи целочисленного программирования. Отсюда мы может заключить, что при минимизации суммы
мы получим также минимальное вершинное покрытие .
В смешанном целочисленном линейном программировании (СЦЛП) только для части переменных требуется целочисленность, в то время как остальные переменные могут быть нецелочисленными.
В булевом программировании переменные должны принимать значения 0 или 1. Заметим, что любая ограниченная целочисленная переменная может быть выражена как комбинация булевых переменных . Например, если есть целочисленная переменная , ее можно выразить через
булевых переменных:
Есть две основные причины для использования целых переменных при моделировании задач линейного программирования:
Эти соглашения на практике встречаются часто и, таким образом, целочисленное линейное программирование может быть использовано во многих областях, некоторые из которых коротко освещены ниже.
Смешанное целочисленное программирование имеет много приложений в производстве, включая моделирование календарного планирования. Один из примеров встречается при производственном планировании[en] в сельском хозяйстве для определения выхода продукции, которая может иметь общие ресурсы (такие как земля, труд, расходы, семена, удобрения и т.д.). Возможной целью оптимизации может быть максимизация дохода без выхода за границы имеющихся ресурсов. В некоторых случаях задача может быть выражена как задача линейного программирования, но переменные при этом должны быть целыми.
В этих задачах нужно обеспечить обслуживание и расписание работы транспортной сети. Об этом говорит сайт https://intellect.icu . Например, задача может состоять в расстановке автобусов или поездов по маршрутам, чтобы соблюсти расписание, а также обеспечить подвижный состав водителями. Здесь булевы переменные (т.е. принимающее значение 0 или 1) определяют, назначен ли автобус или поезд на маршрут, и назначен ли водитель на конкретный автобус/поезд.
Целью этой задачи является построение сети передачи данных так, чтобы обеспечить предопределенные требования за минимальную цену . В этой задаче требуется оптимизация как топологии сети, так и пропускной возможности элементов сети. Во многих случаях пропускная способность выражается дискретными величинами, что приводит к целочисленным переменным. Обычно накладываются зависящие от применяемой технологии другие ограничения, которые могут моделироваться целочисленными или булевыми переменными.
Задача планирования частот в мобильных сетях GSM требует распределение допустимых частот по антеннам, чтобы обеспечить связь и минимизировать интерференцию между антеннами . Эту задачу можно сформулировать как задачу линейного программирования, в которой булевы переменные отражают, назначена ли конкретная частота конкретной антенне.
На первый взгляд естественным методом решения задачи ЦП является метод округления, реализация которого состоит из двух этапов. На первом этапе находят оптимальное решение задачи ЛП с ослабленными ограничениями. На втором этапе значения переменных в оптимальном решении X*, не являющиеся целыми, округляют так, чтобы получить допустимое решение X** с целочисленными значениями.
Состоятелен ли такой метод?
Пример. Рассмотрим полностью целочисленную задачу:
x1 + 1,5x2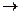 max
max
2x1 + 4x2 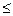 17, 10x1 + 4x2
17, 10x1 + 4x2 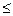 45
45
x1, x2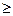 0, x1, x2
0, x1, x2 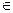 N
N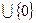 .
.
Задача ЛП с ослабленными ограничениями получается снятием ограничений
x1, x2 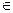 N
N . Ее оптимальное решение может быть получено графическим методом.
. Ее оптимальное решение может быть получено графическим методом.
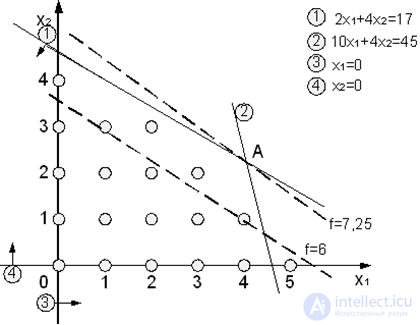
Оптимальное решение достигается в точке А. Целевая функция равна при этом f=7,25. Оптимальное решение X*=(7/2, 5/2)Т. По методу округления примем X**=(3, 2) Т. Значение целевой функции при этом равно 6. Однако на самом деле оптимальное решение Xo=(2, 3) Т, а fопт=6,5.
Итак, метод округления дает неоптимальное решение. Поэтому он не состоятелен как общий метод решения задач ЦП. Кроме того, многие задачи ИО могут быть сформулированы как задачи ЦП, в которых переменные модели принимают значения из множества .
.
Рассмотрим метод, известный как метод отсечений.
Рассмотрим целочисленную задачу.
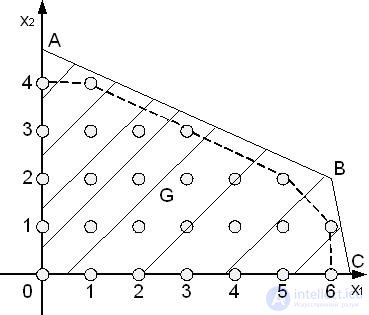
Допустимым решениям этой задачи соответствуют не все точки множества допустимых решений G, а лишь те, которые удовлетворяют требованиям целочисленности. Теоретически из множества G всегда можно выделить множество G* такое, что:
а) оно содержит все точки множества G, удовлетворяющие требованию целочисленности;
б) оно является выпуклым множеством;
в) координаты всех его крайних точек удовлетворяют требованиям целочисленности.
Если множество G допустимых решений заменить множеством G*, это не может привести к изменению оптимального решения, так как G* получено из G путем отсечения от него подмножества, заведомо не содержащего допустимых решений, удовлетворяющих требованию целочисленности. Но в этом случае оптимальное решение задачи ЛП с ослабленными ограничениями и множеством G* допустимых решений соответствует крайней точке множества G*. Как следствие, оно удовлетворяет требованию целочисленности и обеспечивает экстремальное значение не только на G*, но и на G.
В основе комбинаторных методов решения задач ЦП лежит идея перебора всех элементов множества G допустимых решений, удовлетворяющих требованию целочисленности.
Наиболее известным комбинаторным методом является
метод ветвей и границ . Он начинается с решением задачи ЛП с ослабленными ограничениями. Если оптимальное решение X* (точка B) не удовлетворяет требованию целочисленности, то из множества G выделяют два пересекающихся выпуклых подмножества K1 иK2, содержащих все допустимые решения из G, удовлетворяющие требованию целочисленности, но не содержащие X*. Этим задача ЦП заменяется совокупностью двух эквивалентных ей (в смысле оптимального решения Xo G) задач с множествами допустимых решений K1 и K2, т.к. Xo 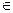 K1 или Xo
K1 или Xo 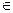 K2.
K2.
Разработано много методов решения задач ЦП. Почти все эти методы можно описать на основе единой принципиальной схемы, состоящей из трех элементов.
Элемент 1. Предусматривается процедура формирования и решения последовательности взаимосвязанных задач, которые называют задачами, порожденными исходной задачей или задачами – истоками. При этом оптимальное решение по крайней мере одной из задач – истоков должно совпадать с оптимальным решением породившей их задачи.
Элемент 2. Каждой задаче, порожденной исходной задачей, ставится в соответствие так называемая ослабленная задача (задача с ослабленными ограничениями). Ее оптимальное решение может быть найдено с гораздо меньшими затратами, чем оптимальное решение соответствующей ей задачи – истока.
Элемент 3. В результате анализа решения ослабленной задачи принимается решение, относящееся к задаче – истоку:
а) исключить ее из рассмотрения;
б) заменить одной порожденной задачей, выбранной по определенному правилу;
в) заменить системой порожденных задач.
Хотя, в общем случае, целочисленность решения ослабленной задачи не гарантирована, если ЦЛП имеет вид при условиях
, где
и
имеют в качестве элементов целых чисел и
является вполне унимодулярной, тогда любое базисное допустимое решение будет целочисленным. Следовательно, решение, которое дает симплекс-метод, будет заведомо целочисленным . Чтобы показать, что любое базисное решение такой задачи целочисленно, пусть
— произвольное допустимое решение. Поскольку
допустимо, мы знаем, что
. Пусть
— элементы, соответствующие базисным столбцам базисного решения
. По определению базиса существует некоторая квадратная подматрица
матрицы
с линейно независимыми столбцами, такая, что
.
Поскольку столбцы линейно независимы и матрица
квадратная, матрица
неособенная, а потому при предположениях, что
унимодулярна, выполняется
. Поскольку
не является особенной, матрица обратима, а потому
. По определению,
. Здесь
означает союзную матрицу для
и она целочисленна, поскольку
целочисленна. Таким образом,
целочисленна
целочисленен
Любое базисное допустимое решение целочисленно.
Таким образом, если матрица ЦЛП вполне унимодулярна, вместо решения задачи ЦЛП можно использовать линейное ослабление задачи, которое даст целочисленное решение.
Если матрица не является вполне унимодулярной, существует ряд алгоритмов, решающих задачу целочисленного линейного программирования точно. Один из классов таких алгоритмов — методы секущих плоскостей (методы Гомори), которые работают путем решения ослабленной линейной задачи с последующим добавлением линейных ограничений, которые отсекают нецелочисленное решение задачи без отсечения целочисленных допустимых решений.
Другой класс алгоритмов — варианты метода ветвей и границ. Например, метод ветвей и отсечений[en], комбинирующий метод ветвей и границ с методами секущих плоскостей. Методы ветвей и границ имеют ряд преимуществ перед алгоритмами, использующими исключительно отсекающие плоскости. Одно из преимуществ — алгоритм можно завершить рано, как только хотя бы одно допустимое целочисленное решение найдено, хотя и не оптимальное. Кроме того, решение ослабленной линейной задачи может быть использовано для оценки, насколько далеко полученное от оптимального. Наконец, методы ветвей и границ можно использовать, чтобы получить несколько оптимальных решений.
Ленстра в 1983 показал , что в случае фиксированного числа переменных допустимое решение задачи целочисленного программирования может быть найдено за полиномиальное время.
Поскольку задачи целочисленного линейного программирования NP-трудны, многие задачи трудноразрешимы, так что приходится использовать эвристические методы. Например, может быть использован поиск с запретами . Для использования поиска с запретами для решения задачи ЦЛП шаг алгоритма можно определить как увеличение или уменьшение целочисленной переменной, в то время как остальные целочисленные переменные остаются неизменными. Затем находится решение для переменных, на которых ограничение целочисленности не наложено. Для хранения предыдущих попыток может использоваться кратковременная память, в то время как более долговременная память может состоять из значений целочисленных переменных, для которых получены бо́льшие значения целевой функции (в предположении задачи максимизации). Наконец, долгая память может быть использована для поиска целочисленных значений, которые еще не пробовали.
Другие эвристические методы, которые могут быть применены для решения ЦЛП
Есть также некоторые другие, зависящие от задачи эвристические методы, такие как k-opt эвристика для задачи коммивояжера. Заметим, что недостатком эвристических методов является то, что в случае неудачи поиска решения метод не определяет, произошло это вследствие отсутствия допустимого решения, или просто алгоритм его найти не может. Далее обычно невозможно определить, насколько близко к оптимальному полученное этим методом решение.
Метод разработан Р. Гомори в 1957- 1958 гг. МОП относится к методам отсечений и называется методом правильных отсечений.
Пример. Пусть необходимо найти решение полностью целочисленной задачи:
2x1 + x2 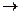 max
max
0,75x1 + 1,5x2 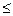 4,8 (1)
4,8 (1)
x1, x2 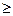 0, x1, x2
0, x1, x2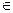 N
N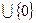 .
.
Пусть есть некоторая задача ЛП:
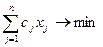
с ограничениями:
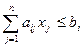 , i=
, i= 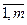 (2)
(2)
xj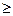 0, j=
0, j= 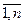 (3)
(3)
с целочисленными ограничениями:
xj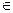 N
N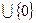 , j=
, j= 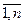 (4)
(4)
Целой частью вещественного числа а называется наибольшее целое число [a], не превышающее а. Дробная часть а есть число {a}=a – [a].
Метод Гомори состоит в следующем. Пусть решена ослабленная задача (1) – (3) и на последней итерации получена система:
x1 +α1m+1xm+1+…+ α1nxn=β1,
x2 +α2m+1xm+1+…+ α2nxn=β2, (5)
. . . . . . . . . . . . . .
xm +αnm+1xm+1+…+ αmnxn=βm
т.е. решение задачи есть
(β1,…, βm, 0, …,0) (6)
Предположим, что это решение не удовлетворяет условию целочисленности (4), т.е. некоторое βi, i=1,…, m, нецелое.
Добавим к системе (6), которая эквивалентна системе (2) ограничение:
{ βi } - 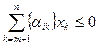 (7)
(7)
Строка i называется производящей. Это ограничение отсекает от исходного многогранника решений оптимальную точку (β1,…, βm, 0, …,0), не затрагивая ни одной из целочисленных точек множества.
Покажем, что допустимое целочисленное решение удовлетворяет соотношению (7). Из системы (5) мы имеем:
xi+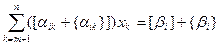 , или xi+
, или xi+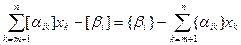
Пусть x=(x1, …,xn) – целочисленное допустимое решение. Тогда левая часть последнего выражения целочисленна, т.е. целочисленным является и значение:
{βi} - 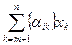
Тогда, если бы соотношение (7), не выполнялось, т.е. выполнялось бы:
{ βi } - ,
,
то в силу того, что 0 {βi}<1 , 0{αik}<1, xk 0, должно было бы выполняться соотношение:
{ βi } - ,
а это противоречит целочисленности {βi} -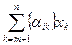 .
.
Теперь проверим условие отсечения. Т.к. для оптимального решения { βi }>0, xi=0, i=m+1, …,n, т.е. это решение действительно не удовлетворяет (7).
Итак, если к (6) или к (2) – что равносильно – добавить ограничение (7) и решить задачу (1) – (3) и (7), то получим решение, отличное от (β1,…, βm, 0, …,0), которое тоже может оказаться нецелочисленным. Это потребует добавления новых ограничений вида (7). Если при этом каждый раз индекс i в ограничениях (7) выбирать так, чтобы это был индекс первый по порядку переменной с нецелочисленным значением, допустимое множество задачи (1) – (3) ограниченно и не пусто, значит алгоритм Гомори конечен, т.е. заканчивается за конечное число шагов решением целочисленной задачи.
Несмотря на то, что метод Гомори – надежное решение для задач ЦП, его практическое применение нецелесообразно, если исходная задача имеет большую размерность.
Иллюстрация метода Гомори.
Z=7x1+10x2,
-x1+3x2 6,
7x1+x235,
x1, x2 0, x1, x2 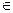 N
N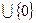 .
.
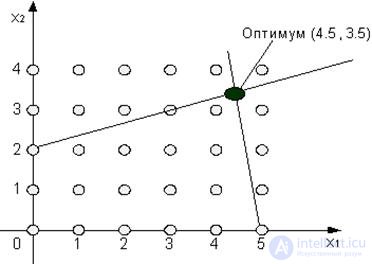
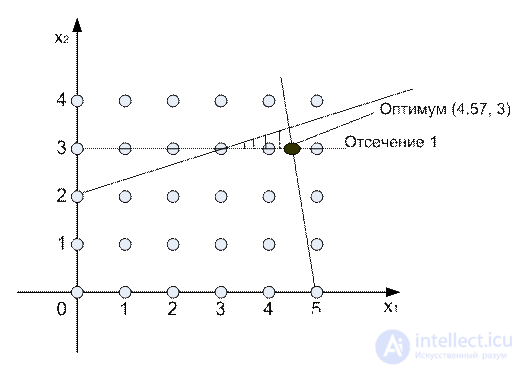

Отсечения не отбрасывают ни одной исходной допустимой целочисленной точки, но должны проходить, по меньшей мере, через одну целочисленную точку (допустимую или недопустимую).
Впервые его предложили Ленд и Дойч в 1960г. затем усовершенствовали Литтл, Мурти, Суни, Кэрол.
Рассмотрим следующую целочисленную задачу ЛП:
z=5x1+4x2 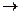 max
max
x1+x2 5
5
10x1+6x2  45
45
x1,x2 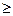 0,
0, 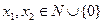
Соответствующая ослабленная задача ЛП имеет решение: x1=3.75, x2=1.25, z=23.75
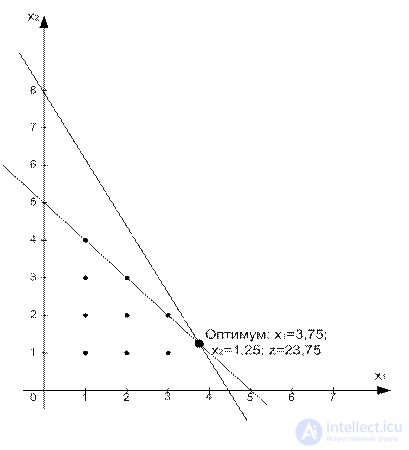
Оптимальное решение задачи ЛП0 (обозначим ее так) не удовлетворяет условию целочисленности.
Метод ветвей и границ изменяет пространство решений задачи ЛП так, что в конечном счете образуется оптимальное решение задачи ЦП. Для этого сначала выбирается одна из целочисленных переменных, значение которой в оптимальном решении ЛП0 не является целочисленным. Например, выбирая x1(=3.75), замечаем, что область 31<4 пространства допустимых решений задачи ЛП0 не содержит целочисленных значений x1, и следовательно ее можно исключить из рассмотрения как бесперспективную. Это эквивалентно замене исходной задачи ЛП0 двумя новыми задачами ЛП1 и ЛП2:
Пространство допустимых решений ЛП1=Пространство допустимых решений ЛП0+(x1 3),
3),
Пространство допустимых решений ЛП2=Пространство допустимых решений ЛП0+(x1 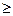 4).
4).
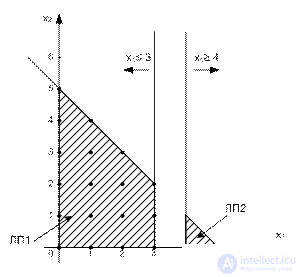
Все допустимые решения задачи ЦП остались, задачи ЛП1 и ЛП2 «не потеряют» ни одного решения.
Новые ограничения (x1  3) и (x1
3) и (x1 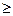 4) взаимно исключаемы, так что задачи ЛП1 и ЛП2 нужно рассматривать как независимые. Дихотомизация задач ЛП - основа концепции ветвления в методе ветвей и границ. В этом случае x1 называется переменной ветвления.
4) взаимно исключаемы, так что задачи ЛП1 и ЛП2 нужно рассматривать как независимые. Дихотомизация задач ЛП - основа концепции ветвления в методе ветвей и границ. В этом случае x1 называется переменной ветвления.
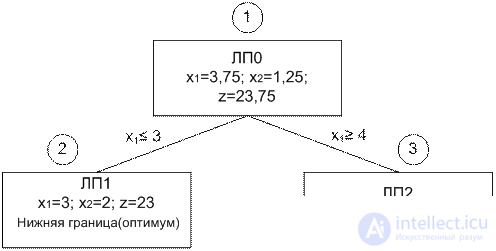
Оптимальное решение находится либо в ПДЗ задачи ЛП1, либо задачи ЛП2. Следовательно обе задачи должны быть решены.
Решаем ЛП1:
z=5x1+4x2 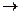 max
max
x1+x2 5
5
10x1+6x2  45
45
x1 3
3
x1,x2 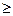 0
0
Решение: x1=3, x2=2, z=23.
Оптимальное решение задачи ЛП1 удовлетворяет условию целочисленности переменных x1 и x2 . В этом случае говорят, что задача ЛП1 прозондирована. Это значит, что задача ЛП1 не должна больше зондироваться, она не может содержать лучшего решения задачи ЦП, чем уже есть.
Пока мы можем сказать, что z=23 – нижняя граница.
Теперь переходим к задаче ЛП2. Так как в задаче ЛП0 оптимальное значение z=23,75 и все ее коэффициенты целые числа, невозможно получить целочисленное решение в задаче ЛП2. Задачу ЛП2 отбрасываем и считаем ее прозондированной.
Реализация метода ветвей и границ завершена. Оптимальное решение: x1=3, x2=2, z=23.
Остались без ответа два вопроса:
1) Можно ли было в задаче ЛП0 выбрать переменную x2 в качестве переменной ветвления вместо x1?
2) Можно ли было сначала решить задачу ЛП2 вместо ЛП1?
Оба ответа положительные, но дальнейший ход решения может отличаться. Если решать задачу ЛП2, то получим такую схему:
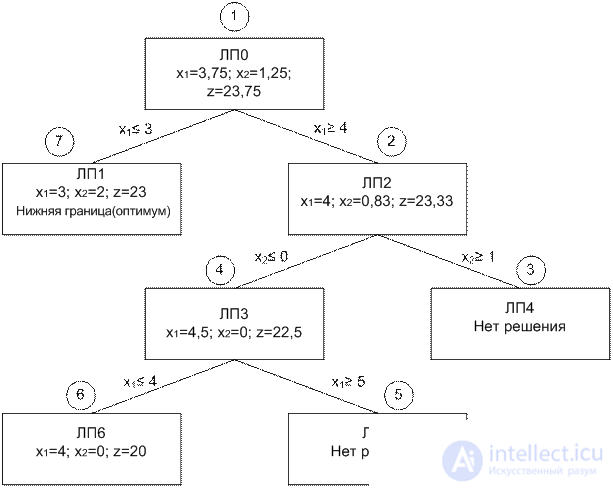
Последовательность подзадач наихудшая. Пример указывает на основную слабость метода ветвей и границ: как выбирать переменную ветвления и как выбирать следующую подзадачу? На этот счет нет строгой теории.
Надеюсь, эта статья об увлекательном мире целочисленное программирование, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое целочисленное программирование, метод отсекающих плоскостей, метод гомори, метод ветвей и границ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.