Лекция
Привет, сегодня поговорим про симплекс-метод, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое симплекс-метод , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
Ограничения. Обозначим x1 и x2 соответственно количество порций пирога и гамбургеров. Можно ограничиться либо 200 фунтами мяса, либо докупить еще. В первом случае ограничение 0,25x1+0,2x2 200, во втором 0,25x1+0,2x2 200.
Естественно, выбор неравенства будет влиять на решение. Так как мы не знаем, какое ограничение необходимо, логично заменить их одним равенством 0,25x1+0,2x2-x3=200, где x3 –свободная переменная. Здесь она играет роль и избыточной, и остаточной.
Целевая функция. Раз надо максимизировать доход, надо продавать как можно больше продукции, то для этого нужны дополнительные закупки мяса, в этом случае x3 должна быть отрицательной, т.е. играть роль избыточной переменной. Для того, чтобы раскрыть «двойственную» природу переменной x3, представим ее в таком виде:
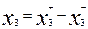 , где
, где 
 0
0
Если 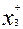 >0 и
>0 и 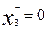 , то переменная x3 играет роль остаточной. Если
, то переменная x3 играет роль остаточной. Если  >0 и
>0 и 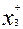 =0, то x3 выступает как избыточная. Итак ограничения теперь имеет вид
=0, то x3 выступает как избыточная. Итак ограничения теперь имеет вид
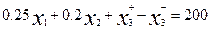 .
.
А целевая функция
Z=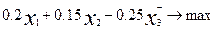
Переход от графического решения к алгебраическому.
Идеи, лежащие в основе графического решения, лежат в основе алгебраического метода, который называется симплекс-метод ом. В графическом методе пространство решений определяется как пересечение полупространств, порождаемых ограничениями. В алгебраическом или симплекс-методе пространство решений задают m линейных уравнений и n неотрицательных переменных.
В алгебраическом представлении количество уравнений m всегда меньше или равно количеству переменных n. (Если количество уравнений m больше количества переменных n, тогда m-n уравнений избыточны.) Если m=n и система уравнений совместна, то она имеет одно решение (если она невырождена), если же m
В алгебраическом представлении кандидаты на оптимальное решение (угловые точки в графическом представлении ) определяются из системы линейных уравнений следующим образом. Пусть m
Пример. Z=2x1+3x2 max
2x1+x2 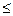 4
4
x1+2x2 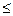 5
5
x1,x2  0.
0.

После преобразования к стандартной форме имеем следующую задачу ЛП.
Z=2x1+3x2 max
2x1+x2+S1 =4,
x1+2x2+S2=5,
x1, x2, S1, S2 0.
Имеем систему из m=2 уравнений для n=4 переменных. Как мы договорились, угловые точки можно определить алгебраически, присвоив n=m=4-2=2 переменным нулевые значения, а затем решив систему относительно m=2 переменных. Если положить x1=0 и x2=2 (точка C).
Какие же переменные полагать равными нулю, чтобы получить угловые точки? Надо просто рассмотреть все комбинации n-m переменных, приравнять их нулю и найти все угловые точки.
В нашем примере мы имеем  угловых точек. На рисунке мы видим только 4. Где же еще две? В действительности точки E и F также являются угловыми точками. Но они еще не кандидаты на оптимальное решение, поскольку не удовлетворяют всем ограничениям.
угловых точек. На рисунке мы видим только 4. Где же еще две? В действительности точки E и F также являются угловыми точками. Но они еще не кандидаты на оптимальное решение, поскольку не удовлетворяют всем ограничениям.
Для полного перехода к алгебраическому методу решения задачи ЛП необходимо как-то назвать угловые точки разного типа. n-m переменных, которые полагают равными нулю называют небазисными переменными. Если оставшиеся m переменных имеют единственное решение, они называются базисными переменными, а совокупность решений, которые они дают составляют базисное решение. Если при этом все переменные принимают неотрицательные значения, такое базисное решение называют допустимым.
|
Небазисные (нулевые) переменные |
Базисные переменные |
Базисные решения |
Угловые точки |
Допустимо ли решение? |
Значение целевой функции Z |
|
(x1, x2) |
(S1, S2) |
(5, 4) |
A |
Да |
0 |
|
(x1, S1) |
(x2, S2) |
(4, -3) |
F |
Нет |
- |
|
(x1, S2) |
(x2, S1) |
(2.5, 1.5) |
D |
Да |
7,5 |
|
(x2, S1) |
(x1, S2) |
(2, 3) |
B |
Да |
4 |
|
(x2, S2) |
(x1, S1) |
(5, -6) |
E |
Нет |
- |
|
(S1, S2) |
(x1, x2) |
(1, 2) |
C |
Да |
8(опт.) |
Из этого примера видно, что при возрастании размерности задачи (n и m) процесс перечисления всех угловых точек задача становится очень сложной задачей. Например, при n=20 и m=10 необходимо решить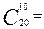 184756 систем уравнений порядка 1010. Это уже устрашающая вычислительная задача. Реально же m и n могут достигать сотен тысяч. Эту проблему снимает симплекс метод.
184756 систем уравнений порядка 1010. Это уже устрашающая вычислительная задача. Реально же m и n могут достигать сотен тысяч. Эту проблему снимает симплекс метод.
Итак, процедура перебора всех базисных решений неэффективна. Рассмотрим симплекс – метод.
Итерационная природа симплекс – метода.
Рассмотрим пространство решений для того же примера.
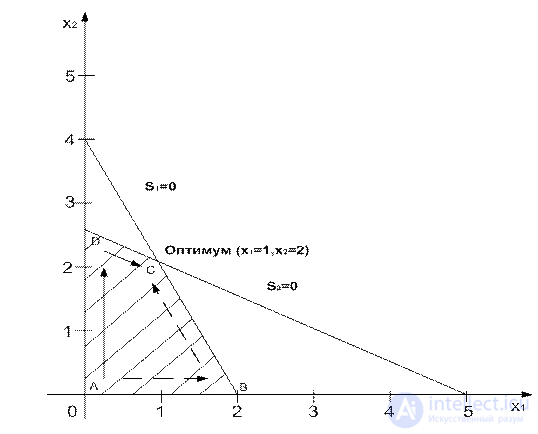
Обычно алгоритм симплекс – метода начинается с исходной точки, где x1=x2=0 (точка A). Об этом говорит сайт https://intellect.icu . В этой начальной точке значение целевой функции Z равно нулю. Возникает вопрос: если одна или обе небазисные переменные x1 и x2 примут положительные значения, приведет ли это к улучшению целевой функции?
Z=2x1+3x2 max.
Очевидно, что если переменная x1 и x2 (или обе сразу ) примут положительные значения, то это приведет к увеличению значения ЦФ.
Однако алгоритм симплекс – метода на каждом шаге допускает изменение значения только одной небазисной переменной.
1. Если увеличивать значение переменной x1, то ее значение должно возрасти так, чтобы соответствовать угловой точке B (кандидаты – только угловые точки). В точкеB симплекс – метод должен увеличить значение переменной x2, перемещаясь в угловую точку C. Т.к. точка C соответствует оптимуму, то процесс заканчивается. Т.о. алгоритм симплекс – метода создает путь A B
B C.
C.
2. Если сначала увеличивать значение переменной x2, то следующей угловой точкой будет точка D, из которой переходим в точку C и заканчиваем процесс A D
D C.
C.
Отметим, что оба пути A B
B C и A
C и A D
D C расположены вдоль границы Г пространства решений. Т.о. симплекс – метод не может сразу перескочить из т.A в т.C.
C расположены вдоль границы Г пространства решений. Т.о. симплекс – метод не может сразу перескочить из т.A в т.C.
Каждую же небазисную переменную сделать положительной в данной угловой точке? Если мы рассматриваем задачу максимизации, то следует выбирать такую небазисную переменную, которая имеет наибольший положительный коэффициент в выражении целевой функции. Если таких переменных несколько, то выбор произволен. Это правило эмпирическое.
Как переводить небазисные переменные в базисные и наоборот при переходе от одной угловой точки к другой?
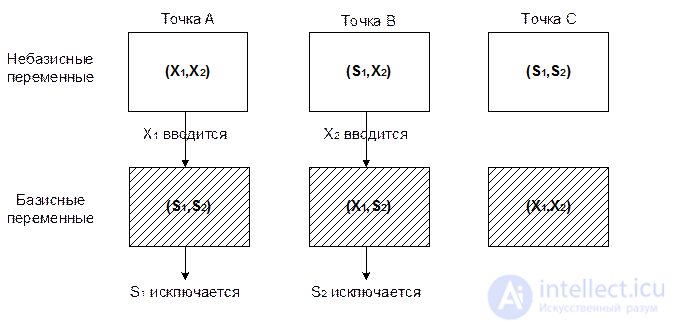
На рисунке показано, что в точке А переменные S1 и S2 являются базисными, а переменные x1 и x2 – небазисными Если переменная x1 принимает положительное значение, мы переходим в угловую точку В, в которой изменяется состояние переменной x1 из небазисной в базисную. Одновременно переменная, которая была базисной в точке А становится небазисной и принимает нулевое значение в точке В. Здесь существенно, сто происходит одновременный «обмен состояниями» между небазисной переменной x1 и базисной S1, что приводит к новым базисным (x1,S2) и небазисным (S1,x2) переменным в точке В. В точке А переменная x1 вводится в базисное решение, а переменная S1 исключается из базисного решения. По терминологии симплекс-метода выбранная небазисная (нулевая) переменная называется вводимой (в базисное решение), а удаляемая (из базисного решения) базисная переменная исключаемой. В т. В вводимой и исключаемой переменными будутсоответственно x2 и S2.
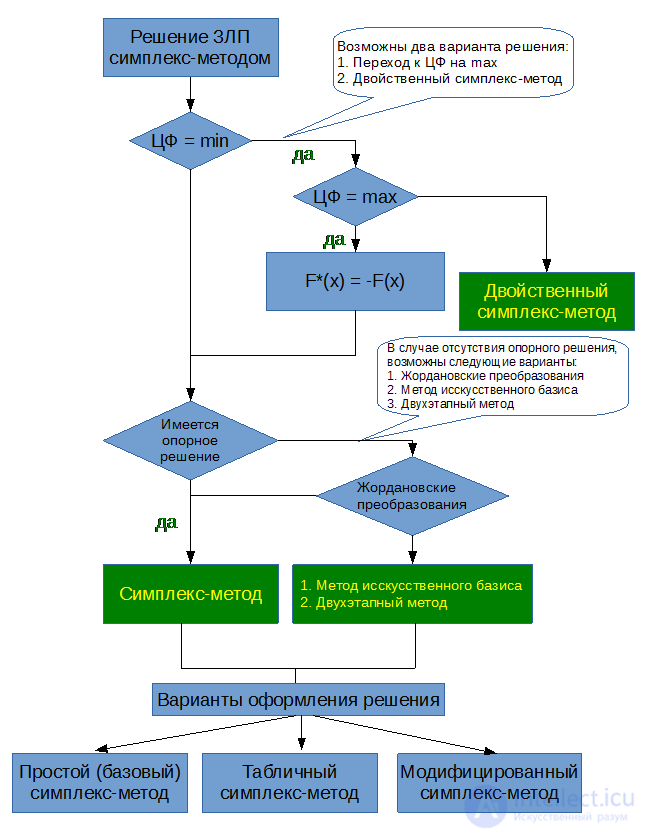
Рассмотрим следующий пример.
Вернемся к задаче про компанию Reddy Mikks. В стандартной форме эта задача запишется так:
Z=5x1+4x2+0S1+0S2+0S3+0S4  max
max
при ограничениях:
6x1+4x2+S1=24
x1+2x2+S2=6
-x1+x2+S3=1
x2+S4=2
x1,x2,S1,S2,S3,S40
Здесь S1,S2,S3,S4 – дополнительные (остаточные) переменные.
Целевую функцию будем представлять в виде уравнения:
Z – 5x1 – 4x2 =0
Задачу ЛП в стандартной форме представим в виде таблицы:
|
Базис |
Z |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Решение |
|
|
Z |
1 |
- 5 |
- 4 |
0 |
0 |
0 |
0 |
0 |
Z-строка |
|
S1 |
0 |
6 |
4 |
1 |
0 |
0 |
0 |
24 |
S1-строка |
|
S2 |
0 |
1 |
2 |
0 |
1 |
0 |
0 |
6 |
S2-строка |
|
S3 |
0 |
-1 |
1 |
0 |
0 |
1 |
0 |
1 |
S3-строка |
|
S4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
S4-строка |
Таблица показывает множества базисных и небазисных переменных, а также решение, соответствующее данной (начальной) итерации. Начальная итерация начинается из точки (x1,x2)=(0,0). Это соответствует следующим множествам базисных и небазисных переменных:
Небазисные (нулевые): (x1,x2)
Базисные: (S1,S2,S3,S4)
Так как x1=0 , x2=0 и коэффициенты при базисных переменных S1,S2,S3,S4 в уравнении целевой функции равны нулю, а в формулах левых частей равенств ограничений – 1, то без дополнительных вычислений имеем: Z=0, S1=24, S2=6, S3=1, S4=0.
В таблице базисные переменные перечислены в левом столбце «Базис», а их значения – в правом столбце «Решение». Таким образом, определена текущая угловая точка.
Поскольку коэффициент при переменной x1 в формуле целевой функции наибольший, ее следует внести в число базисных (она станет вводимой). Из таблицы видно, что вводимая переменная определяется среди множества небазисных как имеющая наибольший отрицательный коэффициент во 2-й строке. Если все коэффициенты во 2-й строке будут неотрицательны, значит достигнут максимум.
Чтобы определить исключаемую переменную, надо вычислить точки пересечения всех функций с положительным направлением оси x1. Эти координаты можно вычислить как отношения правых частей равенства (столбец «Решение») и коэффициентов при переменной x1.
|
Базис |
Коэффициенты при x1 |
Решение |
Отношение (точка пересечения) |
|
S1 |
6 |
24 |
x1=24/6=4 |
|
S2 |
1 |
6 |
x1=6/1=6 |
|
S3 |
-1 |
1 |
x1=1/(-1)=-1 – не подходит |
|
S4 |
0 |
2 |
x1=2/0= – не подходит |
Максимальное неотрицательное соотношение соответствует базисной переменной S2, она определяется как исключаемая (т.е. на следующей итерации ее значение будет равно нулю). Значение вводимой переменной x1 также равно минимальному неотрицательному отношению: x1=6

Максимизировать
Z=5x1+4x2
1) 6x1+4x2+S1=24
2) x1+2x2+S2=6
3) -x1+x2+S3=1
4) x2+S4=2
x1,x2  0
0
Значение целевой функции при этом возрастет до 5 4=20.
4=20.
Замена исключаемой переменной S1 на вводимую переменную x1 приводит к новым множествам базисных и небазисных переменных и к новому решению в т.В.
Небазисные (нулевые) переменные (S1,x2)
Базисные переменные (x1,S2,S3,S4)
Теперь надо выполнить преобразование в таблице, чтобы в столбцах «Базис» и «Решение» получить новое решение, соответствующее точке В.
В следующей таблице, которая пока совпадает с начальной определим ведущий столбец, ассоциируемый с вводимой переменной и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки называется ведущим.
|
Базис |
Z |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Решение |
|
|
Z |
1 |
- 5 |
- 4 |
0 |
0 |
0 |
0 |
0 |
|
|
S1 |
0 |
6 |
4 |
1 |
0 |
0 |
0 |
24 |
Ведущая строка |
|
S2 |
0 |
1 |
2 |
0 |
1 |
0 |
0 |
6 |
|
|
S3 |
0 |
-1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
|
S4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
|
Ведущий столбец
Процесс вычисления нового базисного решения состоит из двух этапов:
1. Вычисление элементов новой ведущей строки.
Новая ВС = Текущая ВС / Ведущий элемент
2. Вычисление элементов остальных строк, включая Z-строку.
Новая строка = Текущая строка – ее коэффициент в ведущем столбце Новая ВС
В примере вычисления таковы:
1. Новая ведущая S1-строка = Текущая ведущая S1-строка / 6
2. Новая Z-строка = Текущая Z-строка – (-5) Новая ВС
3. Новая S2-строка = Текущая S2-строка – (1) Новая ВС
4. Новая S3-строка = Текущая S3-строка – (-1) Новая ВС
5. Новая S4-строка = Текущая S4-строка – (0) Новая ВС
|
Базис |
Z |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Решение |
|
Z |
1 |
0 |
0 |
3/4 |
1/2 |
0 |
0 |
21 |
|
x1 |
0 |
1 |
0 |
1/4 |
-1/2 |
0 |
0 |
3 |
|
x2 |
0 |
0 |
1 |
-1/8 |
3/4 |
0 |
0 |
3/2 |
|
S3 |
0 |
0 |
0 |
3/8 |
-5/4 |
1 |
0 |
5/2 |
|
S4 |
0 |
0 |
0 |
1/8 |
-3/4 |
0 |
1 |
1/2 |
Так как Z-строка не имеет отрицательных коэффициентов, соответствующих небазисным переменным S1 и S2, полученное решение оптимально.
Значения дополнительных переменных S1=S2=0, S3=5/2 и S4=1/2 согласуются со значениями переменных x1 и x2.
C помощью симплекс-таблицы можно получить много дополнительной информации о состоянии ресурсов. Статус «дефицитный» или «недефицитный» для ресурса определяется тем, использован он или нет. Если дополнительная переменная равна нулю, ресурс использован полностью, он получает статус дефицитного.
|
Ресурс |
Остаточная переменная |
Статус |
|
Сырье М1 |
S1=0 |
Дефицитный |
|
Сырье М2 |
S2=0 |
Дефицитный |
Надеюсь, эта статья об увлекательном мире симплекс-метод, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое симплекс-метод и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.