Лекция
Привет, Вы узнаете о том , что такое случайные функции, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое случайные функции, характеристики случайных функций , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Случайной функцией называется функция, которая в результате опыта может принять тот или иной конкретный вид, неизвестно заранее - какой именно. Конкретный вид, принимаемый случайной функцией в результате опыта, называется реализацией случайной функции.
Мы имели много случаев убедиться в том, какое большое значение в теории вероятностей имеют основные числовые характеристики случайных величин: математическое ожидание и дисперсия - для одной случайной величины, математические ожидания и корреляционная матрица - для системы случайных величин. Искусство пользоваться числовыми характеристиками, оставляя по возможности в стороне законы распределения, - основа прикладной теории вероятностей. Аппарат числовых характеристик представляет собой весьма гибкий и мощный аппарат, позволяющий сравнительно просто решать многие практические задачи.
Совершенно аналогичным аппаратом пользуются и в теории случайных функций. Для случайных функций также вводятся простейшие основные характеристики, аналогичные числовым характеристикам случайных величин, и устанавливаются правила действий с этими характеристиками. Такой аппарат оказывается достаточным для решения многих практических задач.
В отличие от числовых характеристик случайных величин, предоставляющих собой определенные числа, характеристики случайных функций представляют собой в общем случае не числа, а функции.
Математическое ожидание случайной функции 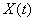 определяется следующим образом. Рассмотрим сечение случайной функции
определяется следующим образом. Рассмотрим сечение случайной функции 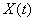 при фиксированном
при фиксированном 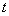 . В этом сечении мы имеем обычную случайную величину; определим ее математическое ожидание. Очевидно, в общем случае оно зависит от
. В этом сечении мы имеем обычную случайную величину; определим ее математическое ожидание. Очевидно, в общем случае оно зависит от 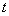 , т. е. представляет собой некоторую функцию
, т. е. представляет собой некоторую функцию 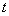 :
:
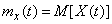 . (15.3.1)
. (15.3.1)
Таким образом, математическим ожиданием случайной функции 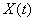 называется неслучайная функция
называется неслучайная функция 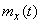 , которая при каждом значении аргумента
, которая при каждом значении аргумента 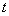 равна математическому ожиданию соответствующего сечения случайной функции.
равна математическому ожиданию соответствующего сечения случайной функции.
По смыслу математическое ожидание случайной функции есть некоторая средняя функция, около которой различным образом варьируются конкретные реализации случайной функции.
На рис. 15.3.1 тонкими линиями показаны реализации случайной функции, жирной линией - ее математическое ожидание.
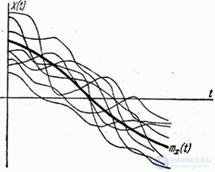
Рис. 15.3.1.
Аналогичным образом определяется дисперсия случайной функции.
Дисперсией случайной функции 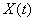 называется неслучайная функция
называется неслучайная функция  , значение которой для каждого
, значение которой для каждого 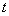 равно дисперсии соответствующего сечения случайной функции:
равно дисперсии соответствующего сечения случайной функции:
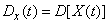 . (15.3.2)
. (15.3.2)
Дисперсия случайной функции при каждом 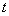 характеризует разброс возможных реализаций случайной функции относительно среднего, иными словами, «степень случайности» случайной функции.
характеризует разброс возможных реализаций случайной функции относительно среднего, иными словами, «степень случайности» случайной функции.
Очевидно,  есть неотрицательная функция. Извлекая из нее квадратный корень, получим функцию
есть неотрицательная функция. Извлекая из нее квадратный корень, получим функцию 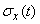 - среднее квадратическое отклонение случайной функции:
- среднее квадратическое отклонение случайной функции:
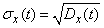 . (15.3.3)
. (15.3.3)
Математическое ожидание и дисперсия представляют собой весьма важные характеристики случайной функции; однако для описания основных особенностей случайной функции этих характеристик недостаточно. Чтобы убедиться в этом, рассмотрим две
случайные функции 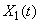 и
и  , наглядно изображенные семействами реализаций на рис. 15.3.2 и 15.3.3.
, наглядно изображенные семействами реализаций на рис. 15.3.2 и 15.3.3.

Рис. 15.3.2.
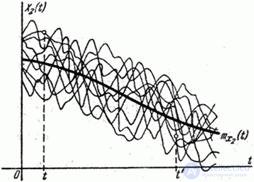
Рис. 15.3.3.
У случайных функций 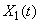 и
и  примерно одинаковые математические ожидания и дисперсии; однако характер этих случайных функций резко различен. Для случайной функции
примерно одинаковые математические ожидания и дисперсии; однако характер этих случайных функций резко различен. Для случайной функции 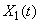 (рис. 15.3.2) характерно плавное, постепенное изменение. Если, например, в точке
(рис. 15.3.2) характерно плавное, постепенное изменение. Если, например, в точке 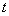 случайная функция
случайная функция 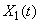 приняла значение, заметно превышающее среднее, то весьма вероятно, что и в точке
приняла значение, заметно превышающее среднее, то весьма вероятно, что и в точке 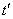 она также примет значение больше среднего. Для случайной функции
она также примет значение больше среднего. Для случайной функции 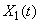 характерна ярко выраженная зависимость между ее значениями при различных
характерна ярко выраженная зависимость между ее значениями при различных 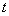 . Напротив, случайная функция
. Напротив, случайная функция  (рис. Об этом говорит сайт https://intellect.icu . 15.3.3) имеет резко колебательный характер с неправильными, беспорядочными колебаниями. Для такой случайной функции характерно быстрое затухание зависимости между ее значениями по мере увеличения расстояния по
(рис. Об этом говорит сайт https://intellect.icu . 15.3.3) имеет резко колебательный характер с неправильными, беспорядочными колебаниями. Для такой случайной функции характерно быстрое затухание зависимости между ее значениями по мере увеличения расстояния по 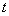 между ними.
между ними.
Очевидно, внутренняя структура обоих случайных процессов совершенно различна, но это различие не улавливается ни математическим ожиданием, ни дисперсией; для его описания необходимо вести специальную характеристику. Эта характеристика называется корреляционной функцией (иначе - автокорреляционной функцией). Корреляционная функция характеризует степень зависимости между сечениями случайной функции, относящимися к различным 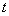 .
.
Пусть имеется случайная функция 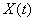 (рис. 15.3.4); рассмотрим два ее сечения, относящихся к различным моментам:
(рис. 15.3.4); рассмотрим два ее сечения, относящихся к различным моментам: 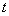 и
и 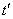 , т. е. две случайные величины
, т. е. две случайные величины 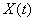 и
и 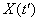 . Очевидно, что при близких значениях
. Очевидно, что при близких значениях 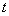 и
и 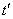 величины
величины 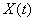 и
и 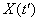 связаны тесной зависимостью: если величина
связаны тесной зависимостью: если величина 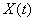 приняла какое-то значение, то и величина
приняла какое-то значение, то и величина 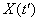 с большой вероятностью примет значение, близкое к нему. Очевидно также, что при увеличении интервала между сечениями
с большой вероятностью примет значение, близкое к нему. Очевидно также, что при увеличении интервала между сечениями 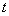 ,
, 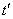 зависимость величин
зависимость величин 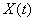 и
и 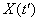 вообще должна убывать.
вообще должна убывать.
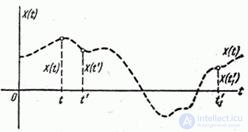
Рис. 15.3.4.
Степень зависимости величин  и
и 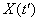 может быть в значительной мере охарактеризована их корреляционным моментом; очевидно, он является функцией двух аргументов
может быть в значительной мере охарактеризована их корреляционным моментом; очевидно, он является функцией двух аргументов 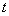 и
и 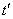 . Эта функция и называется корреляционной функцией.
. Эта функция и называется корреляционной функцией.
Таким образом, корреляционной функцией случайной функции 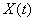 называется неслучайная функция двух аргументов
называется неслучайная функция двух аргументов 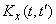 , которая при каждой паре значений
, которая при каждой паре значений 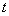 ,
, 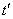 равна корреляционному моменту соответствующих сечений случайной функции:
равна корреляционному моменту соответствующих сечений случайной функции:
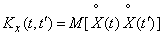 , (15.3.4)
, (15.3.4)
где
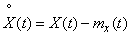 ,
,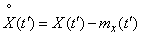 .
.
Вернемся к примерам случайных функций 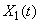 и
и  (рис. 15.3.2 и 15.3.3). Мы видим теперь, что при одинаковых математических ожиданиях и дисперсиях случайные функции
(рис. 15.3.2 и 15.3.3). Мы видим теперь, что при одинаковых математических ожиданиях и дисперсиях случайные функции 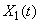 и
и  имеют совершенно различные корреляционные функции. Корреляционная функция случайной функции
имеют совершенно различные корреляционные функции. Корреляционная функция случайной функции 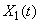 медленно убывает по мере увеличения промежутка
медленно убывает по мере увеличения промежутка 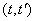 ; напротив, корреляционная функция случайной функции
; напротив, корреляционная функция случайной функции  быстро убывает с увеличением этого промежутка.
быстро убывает с увеличением этого промежутка.
Выясним, во что обращается корреляционная функция 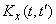 , когда ее аргументы совпадают. Полагая
, когда ее аргументы совпадают. Полагая 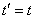 , имеем:
, имеем:
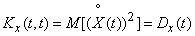 , (15.3.5)
, (15.3.5)
т. е. при 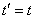 корреляционная функция обращается в дисперсию случайной функции.
корреляционная функция обращается в дисперсию случайной функции.
Таким образом, необходимость в дисперсии как отдельной характеристике случайной функции отпадает: в качестве основных характеристик случайной функции достаточно рассматривать ее математическое ожидание и корреляционную функцию.
Так как корреляционный момент двух случайных величин 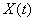 и
и 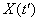 не зависит от последовательности, в которой эти величины рассматриваются, то корреляционная функция симметрична относительно своих аргументов, т. е. не меняется при перемене аргументов местами:
не зависит от последовательности, в которой эти величины рассматриваются, то корреляционная функция симметрична относительно своих аргументов, т. е. не меняется при перемене аргументов местами:
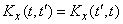 . (15.3.6)
. (15.3.6)
Если изобразить корреляционную функцию 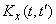 в виде поверхности, то эта поверхность будет симметрична относительно вертикальной плоскости
в виде поверхности, то эта поверхность будет симметрична относительно вертикальной плоскости  , проходящей через биссектрису угла
, проходящей через биссектрису угла 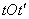 (рис. 15.3.5).
(рис. 15.3.5).

Рис. 15.3.5.
Заметим, что свойства корреляционной функции естественно вытекают из свойств корреляционной матрицы системы случайных величин. Действительно, заменим приближенно случайную функцию 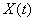 системой
системой 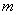 случайных величин
случайных величин 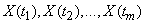 . При увеличении
. При увеличении 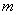 и соответственном уменьшении промежутков между аргументами корреляционная матрица системы, представляющая собой таблицу о двух входах, в пределе переходит в функцию двух непрерывно изменяющихся аргументов, обладающую аналогичными свойствами. Свойство симметричности корреляционной матрицы относительно главной диагонали переходит в свойство симметричности корреляционной функции (15.3.6). По главной диагонали корреляционной матрицы стоят дисперсии случайных величин; аналогично при
и соответственном уменьшении промежутков между аргументами корреляционная матрица системы, представляющая собой таблицу о двух входах, в пределе переходит в функцию двух непрерывно изменяющихся аргументов, обладающую аналогичными свойствами. Свойство симметричности корреляционной матрицы относительно главной диагонали переходит в свойство симметричности корреляционной функции (15.3.6). По главной диагонали корреляционной матрицы стоят дисперсии случайных величин; аналогично при 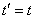 корреляционная функция
корреляционная функция 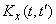 обращается в дисперсию
обращается в дисперсию  .
.
На практике, если требуется построить корреляционную функцию случайной функции 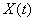 , обычно поступают следующим образом: задаются рядом равноотстоящих значений аргумента и строят корреляционную матрицу полученной системы случайных величин. Эта матрица есть не что иное, как таблица значений корреляционной функции для прямоугольной сетки значений аргументов на плоскости
, обычно поступают следующим образом: задаются рядом равноотстоящих значений аргумента и строят корреляционную матрицу полученной системы случайных величин. Эта матрица есть не что иное, как таблица значений корреляционной функции для прямоугольной сетки значений аргументов на плоскости 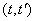 . Далее, путем интерполирования или аппроксимации можно построить функцию двух аргументов
. Далее, путем интерполирования или аппроксимации можно построить функцию двух аргументов 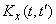 .
.
Вместо корреляционной функции 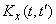 можно пользоваться нормированной корреляционной функцией:
можно пользоваться нормированной корреляционной функцией:
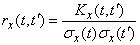 , (15.3.7)
, (15.3.7)
которая представляет собой коэффициент корреляции величин 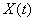 ,
, 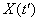 . Нормированная корреляционная функция аналогична нормированной корреляционной матрице системы случайных величин. При
. Нормированная корреляционная функция аналогична нормированной корреляционной матрице системы случайных величин. При 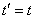 нормированная корреляционная функция равна единице:
нормированная корреляционная функция равна единице:
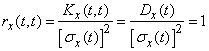 . (15.3.8)
. (15.3.8)
Выясним, как меняются основные характеристики случайной функции при элементарных операциях над нею: при прибавлении неслучайного слагаемого и при умножении на неслучайный множитель. Эти неслучайные слагаемые и множители могут быть как постоянными величинами, так в общем случае и функциями 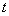 .
.
Прибавим к случайной функции 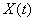 неслучайное слагаемое
неслучайное слагаемое  . Получим новую случайную функцию:
. Получим новую случайную функцию:
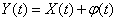 . (15.3.9)
. (15.3.9)
По теореме сложения математических ожиданий:
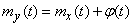 , (15.3.10)
, (15.3.10)
т. е. при прибавлении к случайной функции неслучайного слагаемого к ее математическому ожиданию прибавляется то же неслучайное слагаемое.
Определим корреляционную функцию случайной функции 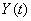 :
:
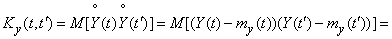
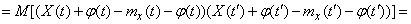
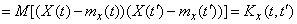 , (15.3.11)
, (15.3.11)
т. е. от прибавления неслучайного слагаемого корреляционная функция случайной функции не меняется.
Умножим случайную функцию 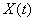 на неслучайный множитель
на неслучайный множитель  :
:
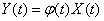 . (15.3.12)
. (15.3.12)
Вынося неслучайную величину  за знак математического ожидания, имеем:
за знак математического ожидания, имеем:
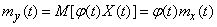 , (15.3.13)
, (15.3.13)
т. е. при умножении случайной функции на неслучайный множитель ее математическое ожидание умножается на тот же множитель.
Определяем корреляционную функцию:
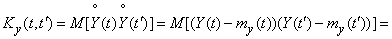
 , (15.3.14)
, (15.3.14)
т. е. при умножении случайной функции на неслучайную функцию  ее корреляционная функция умножается на
ее корреляционная функция умножается на 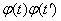 .
.
В частности, когда 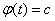 (не зависит от
(не зависит от 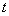 ), корреляционная функция умножается на
), корреляционная функция умножается на 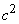 .
.
Пользуясь выведенными свойствами характеристик случайных функций, можно в ряде случаев значительно упростить операции с ними. В частности, когда требуется исследовать корреляционную функцию или дисперсию случайной функции, можно заранее перейти от нее к так называемой центрированной функции:
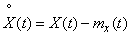 . (15.3.15)
. (15.3.15)
Математическое ожидание центрированной функции тождественно равно нулю, а ее корреляционная функция совпадает с корреляционной функцией случайной функции 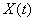 :
:
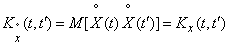 . (15.3.16)
. (15.3.16)
При исследовании вопросов, связанных с корреляционными свойствами случайных функций, мы в дальнейшем всегда будем переходить от случайных функций к соответствующим центрированным функциям, отмечая это значком  вверху знака функции.
вверху знака функции.
Иногда, кроме центрирования, применяется еще нормирование случайных функций. Нормированной называется случайная функция вида:
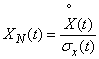 . (15.3.17)
. (15.3.17)
Корреляционная функция нормированной случайной функции 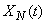 равна
равна
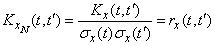 , (15.3.18)
, (15.3.18)
а ее дисперсия равна единице.
Информация, изложенная в данной статье про случайные функции , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое случайные функции, характеристики случайных функций и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ